Калькулятор вклада с капитализацией, пополнением, частичным снятием, пролонгацией
Содержание:
- Примеры сложных процентов в инвестициях
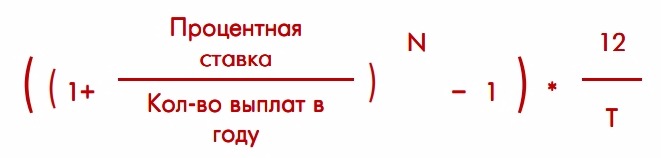
- Общая формула расчета процентов по вкладу
- Что из себя представляют сложные проценты?
- Ключевые составляющие сложных процентов
- Формулы сложных процентов по вкладам и примеры решения задач
- Подробнее о сложном проценте
- Простые проценты
- Вспомогательные формулы
- Что такое сложный процент в инвестициях простыми словами
- Пример сложного процента на банковском депозите
- Послесловие
- Формулы расчета
- Заключение
Примеры сложных процентов в инвестициях
Можно смело сказать, что каждый рубль отложенный сегодня принесёт десятки рублей через 10 лет за счёт постоянного реинвестирования прибыли. Подобным образом разбогатели многие миллиардеры (Уоррен Баффет).
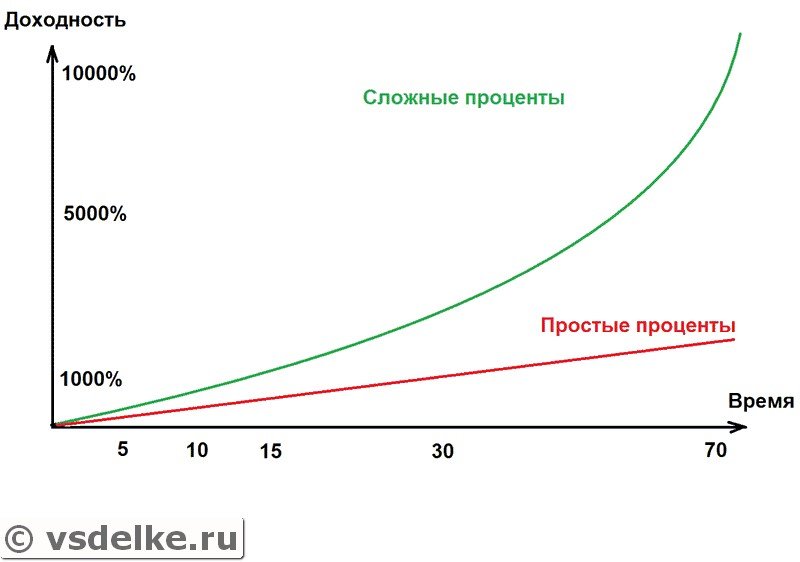
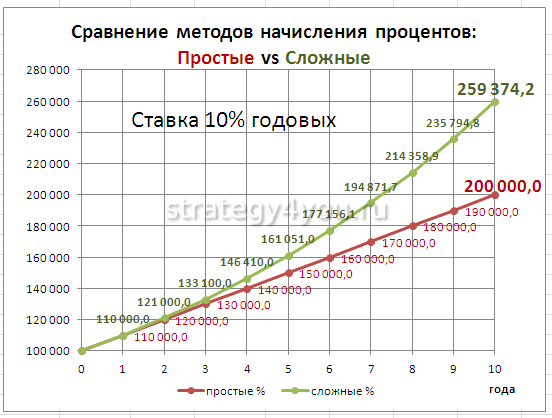
Обратите внимание, что эффект заметен со временем все сильнее и в конце кривая сложных процентов приобретает экспоненциальный характер, в то время как простые проценты растут линейно. Рассмотрим на примерах этот принцип
2.1. Пример: инвестируем ежемесячно в банк под 8% (срок 10 лет)
Если откладывать ежемесячно по 10 тысяч рублей «под подушку» или просто на банковский счёт, то через 10 лет (120 месяцев) сумма будет 1.2 млн рублей (120 умножаем на 10 тыс).
Если же откладывать эти деньги на банковский вклад под 8% годовых, то сумма по истечению 10 лет будет значительно больше: 1 851 738 рублей. Чистый доход от процентов 641 738 рублей (чуть больше 50% за все время).
Новички по ошибке могут получить неправильную сумму, если просто прибавить 8% к отложенной сумме, но это неверно. Сложный процент можно посчитать лишь на онлайн калькуляторе или самостоятельно с помощью длительных вычислений.
Расчёты на калькуляторе сложных процентов:
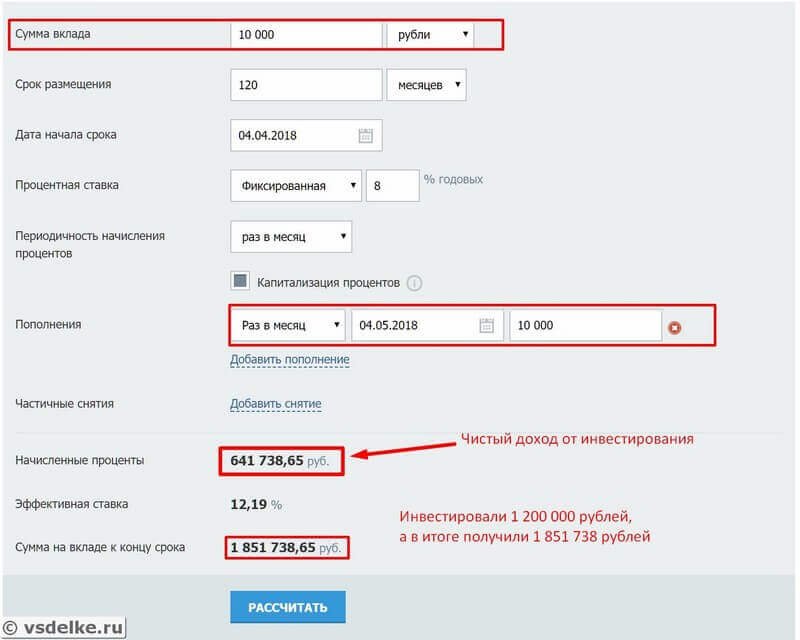
Выписка по балансу:
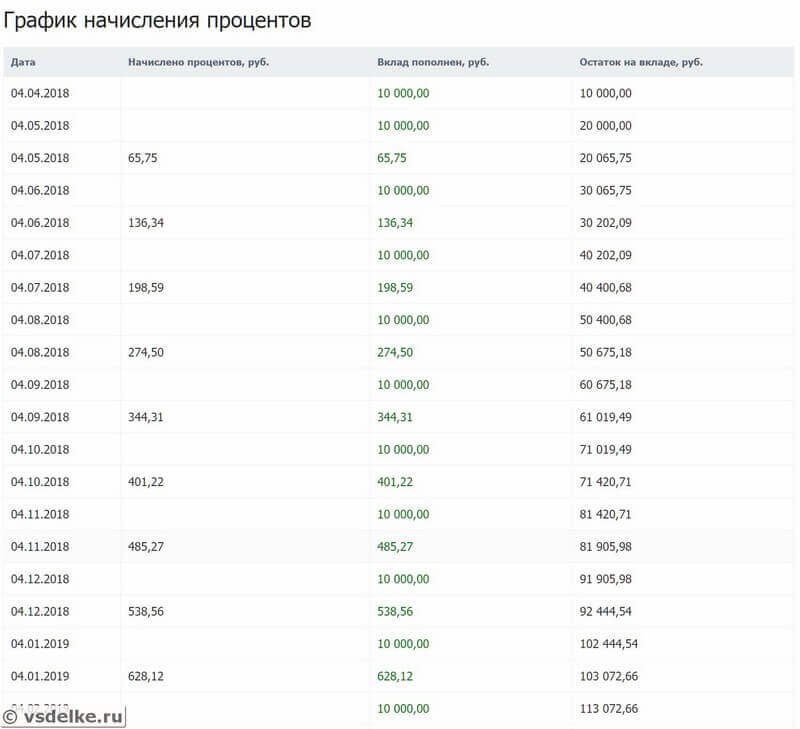
Примечание
В некоторые периоды можно найти ставку на вкладах гораздо выше 8% и доход был бы в таком случае был заметно больше.
2.2. Пример: инвестируем в банк под 8% (срок 20 лет)
Теперь увеличим срок нашего инвестирования с 10 лет до 20 лет. Мы будем также откладывать по 10 тысяч рублей и всю полученную прибыль реинвестировать. Теперь по истечению срока сумма будет 5 938 760 рублей вместо 2 400 000. Чистый доход от процентов 3 528 760. Эта сумма больше всех суммарных вложений в 1.5 раза (150% прибыли за все время)!
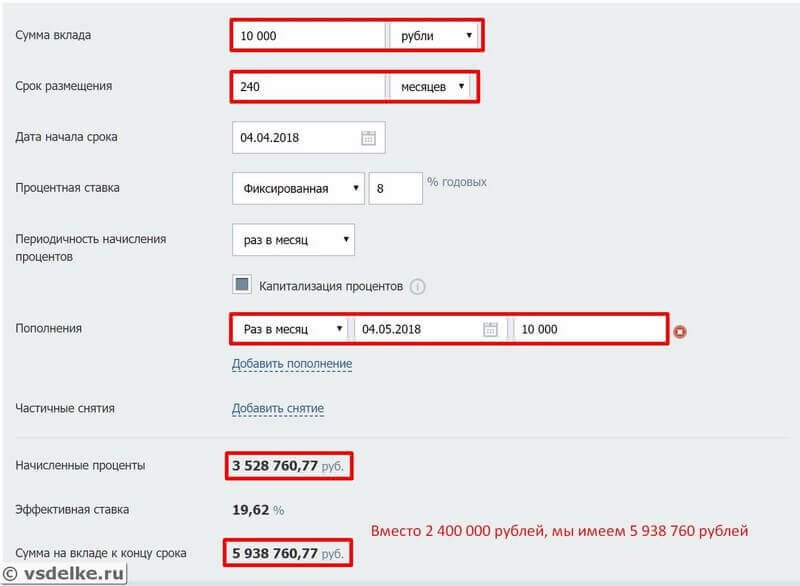
Это наглядный пример того, что чем больший период мы рассматриваем, тем заметнее будет действие сложных процентов.
2.3. Пример: инвестируем в ценные бумаги под 12% (срок 20 лет)
Последний пример депозита. Откладываем по 10 тысяч рублей ежемесячно на протяжении 20 лет, но теперь мы инвестируем деньги в акции и небольшую часть в облигации.
Как показала реальная история, такой инвестиционный портфель в среднем за год приносит 12% с учётом дивидендов от акций при самой простой стратегии «купи и держи».
Итого, сумма на конец срока: 9 999 681 рублей. Чистый доход 7 589 681 рублей. И это не результат везения, не фантастика, а очень реальные цифры дохода, которые доступны каждому лицу. По факту можно даже получить и больше и даже за более короткий срок, если выйти с рынка на его пике, а докупиться в конце цикла падения, но для подобных «маневров» необходимы основы трейдинга и немного времени на совершение торговых операций.
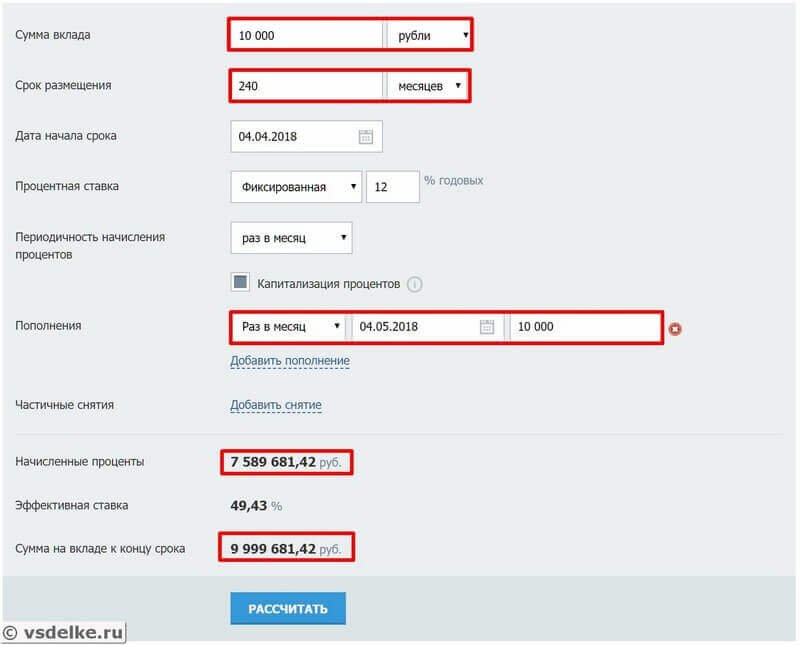
Хочу подчеркнуть, что мы рассмотрели реальные варианты без каких-либо везений и прочее. Такого результата добьется каждый, кто просто вложит в ценные бумаги и не будет дергаться и пытаться что-то ещё сделать. Такая стратегия называется: пассивное индексное инвестирование.
Примечание
При инвестировании в зарубежные акции доход был бы ещё больше (где-то в два раза), поскольку по статистике рубль обесценивается к доллару примерно на 100% каждые 20 лет.
Также важно откладывать в начале как можно больше. Это сильно повышает будущую доходность
Теперь, понимая силу сложных процентов, поговорим о том, во что лучше всего вложить деньги, чтобы получать пассивный доход. Какие конкретно варианты инвестирования существуют, каковы их риски и преимущества можно прочитать:
Общая формула расчета процентов по вкладу
Использование формулы простых процентов целесообразно в случае начисления процентов в конце срока размещения депозита или если они будут переводиться на отдельный счет – если капитализация договором не предусмотрена.
Если средства размещаются на длительный срок и сумма большая, банк использует формулу простых процентов: сумма дохода с процентов занижается.
В этом случае используется формула следующего вида:
S = (P x I x t / K) / 100
Обозначения:
S – конечная сумма, полученная по завершению действия депозита;
P – сумма изначально внесенная на депозит;
I – размер % ставки (за год);
t – кол-во дней начисления %;
K – кол-во дней за год по календарю.
Для расчета сложных процентов, которые применяются в случае капитализации в течение всего периода действия депозитного договора (каждый месяц, раз в квартал, ежедневно), нужно применить следующую формулу:
S = (P x I x j / K) / 100
Эти символы имеют следующее значение:
I – % ставка за год;
J – сумма дней по календарю за конкретный период, на протяжении которого финансовое учреждение капитализирует проценты, начисляемые по выбранному виду вклада;
К – количество дней в году по календарю;
P – изначально привлеченная сумма для размещения на вкладе, в дальнейшем это будет сумма, в которую уже учитываются капитализированные процентные начисления;
S – сумма, которая должна быть выплачена клиенту финучреждения, в ней уже учтены капитализированные %.
Что из себя представляют сложные проценты?

Сложные проценты – это проценты по депозиту или займу, учитывающие как вашу первоначальную сумму, так и проценты, накопленные этой суммой за предыдущие периоды. Поскольку вы зарабатываете проценты не только на основную сумму каждый период, но и на накопленную сумму, вы получаете больше прибыли от вложенных средств.
Со сложными процентами вы добавляете заработанные проценты обратно на свой основной баланс, и затем это приносит вам еще больше процентов, тем самым увеличивая вашу прибыль.
Допустим, у вас есть 1000 долларов на сберегательном счете, на который вы получаете 5% годовых. В первый год вы заработаете 50 долларов, в итоге ваш баланс составит 1050 долларов. Во второй год вы заработаете 5% на балансе в 1050 долларов, что составляет 52,50 доллара, что даст вам новый баланс в размере 1102,50 долларов в конце второго года.
Благодаря магии сложных процентов рост баланса вашего сберегательного счета со временем будет ускоряться, поскольку вы зарабатываете проценты на все более крупных остатках. Если вы оставите 1000 долларов на сберегательном счете на 30 лет, продолжая получать 5% годовых и никогда не добавляете ни копейки на счет, в итоге вы получите остаток в размере 4321,94 доллара.
Проценты могут быть увеличены или добавлены обратно в основную сумму в разные промежутки времени. Например, проценты могут начисляться ежегодно, ежемесячно, ежедневно или даже постоянно. Чем чаще начисляются проценты, тем быстрее растет баланс вашего счета.
Если вы начали с остатком на сберегательном счете в 1000 долларов, но заработанные вами проценты увеличивались ежедневно, а не ежегодно, через 30 лет вы получите общий баланс в размере 4481,23 доллара. Вы заработали бы дополнительно 160 долларов за счет более частого начисления процентов.
Ключевые составляющие сложных процентов
При расчете сложных процентов вам необходимо учитывать несколько ключевых факторов. Каждый из них играет свою роль в конечном продукте, и некоторые переменные могут существенно повлиять на вашу прибыль. Вот пять ключевых переменных, влияющих на понимание сложных процентов:
- Процентная ставка. Процентная ставка, которую вы зарабатываете или взимаете. Чем выше процентная ставка, тем больше денег вы зарабатываете и тем больше вы должны.
- Стартовый принципал. С какой суммы вы начинаете? Насколько крупный кредит вы взяли? Хотя со временем начисление сложных процентов суммируется, все зависит от начальной суммы.
- Частота начисления. Скорость начисления процентов – ежедневно, ежемесячно или ежегодно – определяет, насколько быстро растет баланс. Взяв ссуду или открывая сберегательный счет, убедитесь, что вы понимаете, как часто возрастают проценты.
- Продолжительность. Как долго вы ожидаете удерживать счет или погасить ссуду? Чем дольше вы оставляете деньги на сберегательном счете или чем дольше вы держите долг, тем дольше он будет накапливаться и тем больше вы заработаете или будете должны.
- Депозиты и снятие средств. Ожидаете ли вы регулярно пополнять свой счет? Как часто вы будете платить по кредиту? Скорость, с которой вы увеличиваете свой основной баланс или выплачиваете ссуду, имеет большое значение в долгосрочной перспективе.
В случае сложных процентов прибыль от актива, такая как прирост капитала или реинвестированные дивиденды, со временем приводит к дальнейшему росту прибыли. Инвестиции продолжат приносить прибыль от основной суммы долга и прибыли, накопленной за предыдущие периоды.
Например, реинвестирование денежных дивидендов на покупку большего количества акций увеличит вашу прибыль благодаря будущим выплатам дивидендов
Обратите внимание, что сложные проценты работают как для активов, так и для обязательств
Чтобы рассчитать будущую стоимость инвестиции через эффект сложного процента при определенной норме прибыли за период, вы можете использовать следующую формулу:
FV = PV x (1 + i) ^ n
- FV = будущая стоимость
- PV = текущая стоимость
- i = норма доходности / процентная ставка за период
- n = количество периодов в году
Если вы инвестируете 100000 долларов и хотите знать, какой размер будут иметь ваши инвестиции, исходя из годовой прибыли в размере 8%, которая увеличивается за 10 лет, вот решение, использующее приведенную выше формулу:
FV = 100 000 долларов США x (1 + 0,08) ^ 10
FV = 215 892,50 долл. США
Прибыль = 115 892,50 $
Чтобы продемонстрировать истинную силу начисления сложных процентов, вы можете использовать тот же пример, что и выше, но применять ставку 8% простых процентов на основную сумму каждый год.
Прибыль = 100 000 долларов США x 0,08 x 10 = 80 000 долларов США
Как видите, разница в прибыли между двумя типами инвестиций значительна. Через десять лет разрыв составляет 35 892,50 доллара, или на 44,87% больше при начислении сложных процентов, чем при получении простых процентов.
Если у вас есть хорошо сбалансированный инвестиционный план, вы можете использовать силу сложных процентов, чтобы значительно ускорить свой путь к своим финансовым целям.
Формулы сложных процентов по вкладам и примеры решения задач
Формулы сложных процентов в математике встречаются постоянно, особенно если речь идёт об экономических задачах. Представьте, что вам нужно рассчитать прибыль от банковского вклада за несколько лет. Для этого понадобится такая информация:
- начальная сумма вклада (K нулевая или К)
- ставка доходности (R) — переводится из процентов в число (10% = 0.1)
- количество периодов реинвестирования, то есть лет (n)
А конечную сумму вклада мы назовем просто K. Её можно рассчитать по формуле:
Конечная сумма при расчёте сложных процентов по вкладу
Пример задачи: Инвестор П. положил на депозит в банке 10000$ под 10% годовых. Какую прибыль он получит через 5 лет?
Для начала, давайте узнаем конечную сумму вклада по формуле:
K = 10000$ * (1 + 0.1)5 = 16105.1$
Прибыль (P) — это разница между конечной и стартовой суммой вклада. Считаем:
P = K — К = 16105.1$ — 10000$ = 6105.1$
Можно даже подсчитать прибыль в процентах, для этого нужно найти не разницу, а отношение между конечной и стартовой суммой:
P (%) = K/К — 1 = 16105.1$ / 10000$ — 1= 61.05%
Используя формулу сложных процентов, вы всегда можете предсказать результат инвестирования в будущем. Впрочем, бывают ситуации, когда вам нужно узнать не конечную, а стартовую сумму вклада. Её можно найти по той же формуле сложных процентов по вкладам, но надо немного её изменить:
Формула расчёта сложных процентов для поиска стартовой суммы вклада
Пример задачи: Инвестор В. хочет узнать, сколько ему надо вложить рублей под 20% годовых сейчас, чтобы через 3 года стать рублёвым миллионером.
Используем формулу:
К = 1000000₽ / (1 + 0.2)3 = 578703.7₽
Кроме суммы вклада, через формулу можно найти и остальные параметры. Например, зная стартовую и конечную сумму, можно узнать процентную ставку или количество периодов реинвестирования.
Начнем с процентной ставки:
Формула расчёта сложных процентов по вкладу для поиска нужной процентной ставки
Пример задачи: Инвестор Р. хочет выяснить, вклад с какой процентной ставкой ему нужен, чтобы заработать 10000$ за 3 года, изначально вложив 20000$.
Для начала нужно посчитать конечную сумму, так как мы знаем только прибыль:
K = К+ P = 20000$ + 10000$ = 30000$
А теперь можно использовать формулу:
R = (30000$ / 20000$) ^ 1/3 — 1 = 14.47%
Чтобы получить такую доходность, банковский депозит не подойдёт, а вот консервативный ПАММ-счёт — вполне.
Напоследок давайте выясним, как рассчитать, на какой срок нужно положить деньги, чтобы получить нужную нам прибыль. Без логарифмов не обойтись:
Расчёт сложных процентов по вкладу — поиск нужного количества периодов реинвестирования
Пример задачи: сколько лет нужно держать деньги на депозите в банке под 25% годовых, чтобы 50000 рублей превратить в 100000?
Подставляем в формулу:
n = log1+0.25 100000/50000 = 3.11 лет
Кстати, если речь идёт о банке, то 3.11 лет округляются до 4 — вы обычно не можете снять свои деньги до окончания периода действия вклада. Условия конкретного инвестиционного инструмента всегда стоит учитывать при решении подобных задач.
Кроме рассмотренных нами задач существуют и более сложные. Например, довольно распространённая история — у инвестора есть вклад с возможностью пополнения. Часть каждой зарплаты отправляется туда и надо выяснить, какой же будет результат по итогам.
Пример задачи: Инвестор З. вложил 1000$ и откладывает 50$ каждый месяц. Процентная ставка — 1% в месяц. Какая сумма накопится через 5 лет?
Чтобы узнать результат, нужно создать табличку:
Расчёт результатов инвестирования с доливками, с учётом сложных процентов
В первый месяц сумма инвестиций составила 1000$, на неё начислен 1% — итого 1010$. Во второй месяц работают уже 1010$ и еще 50$, которые инвестор внёс дополнительно. Итого — 1070.10. И так далее…
Разумеется, считать эти таблички каждый раз — довольно напряжно, решать логарифмы — тем более. Поэтому специально для вас при помощи программы Microsoft Excel я сделал небольшой файлик для решения задач по сложным процентам.
Подробнее о сложном проценте
Простые проценты нам больше не интересны, а формула сложного выглядит так:
Давайте теперь посчитаем на суммах и процентах более приближенных к реальности, чтобы ощутить разницу в полной мере.
Задача №1
Дано:
- банковский депозит на сумму 100 тыс. руб.
- процентная ставка 8% годовых
- срок 4 года
- присутствует ежегодная капитализация процентов
Нужно найти:
конечную результирующую сумму (доход + %)
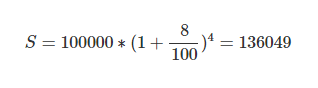
В данном случае происходит ежегодная капитализация процента по вкладу. В некоторых банках также бывает услуга ежемесячной капитализации процентов. Об этом в задаче ниже.
Задача №2
Дано:
- банковский депозит на сумму 100 тыс руб.
- процентная ставка 8% годовых
- период 4 года
- ежемесячная капитализация
Нужно найти:
конечную результирующую сумму (доход + %)
В формуле нужно применять ежемесячный процент, для этого 8 разделим на 12 месяцев. Получается 0,67% — это процент за месяц
И обратите внимание, степень теперь равна 48 — это количество месяцев за 4 года. Подставляем его в формулу:
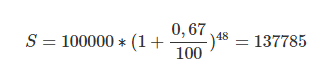
Простые проценты
На практике применяются три варианта расчета простых процентов:
- точные проценты с точным числом дней ссуды (английская практика). Обозначается как 365/365 или АТС/АТС.
- обыкновенные (коммерческие) проценты с точным числом дней ссуды (французская практика). Обозначается как 365/360 или АТС/360.
- обыкновенные проценты с приближенным числом дней ссуды (германская практика). Обозначается как 360/360.
По схеме 360 количество дней к году принимается равным 360 (в каждом месяце по 30 дней).
Пример. Определить приближённое число дней между 12.02.2019 и 27.08.2020.
Если год рассматривается как промежуток, содержащий 12 месяцев продолжительностью 30 дней (дивизор равен 360 дней), то приближённое число дней рассчитывается следующим образом:
где y — номер года, m — номер месяца в году, d — номер дня в месяце.
n = 360*(2020-2019)+30*(8-2)+(27-12) = 555 дней
Pin
Когда срок финансовой сделки не равен целому числу лет:
S=P·(1+tT·i)
где t — срок в днях, T — временная база (365 или 360)
Примеры задач на простые проценты
Решить
-
Ссуда в размере P = 1 млн.руб. выдана d1 = 20.01 до d2 = 05.10 включительно под i = 18% годовых. Какую сумму должен заплатить должник в конце срока при начислении простых процентов? При решении применить три метода расчёта срока ссуды.
Начальная дата: 20.01, конечная дата: 05.10, количество дней между датами: 258
Январь, 11 дней: с 21.01 по 31.01
Февраль, 28 дней: с 01.02 по 28.02
Март, 31 день: с 01.03 по 31.03
Апрель, 30 дней: с 01.04 по 30.04
Май, 31 день: с 01.05 по 31.05
Июнь, 30 дней: с 01.06 по 30.06
Июль, 31 день: с 01.07 по 31.07
Август, 31 день: с 01.08 по 31.08
Сентябрь, 30 дней: с 01.09 по 30.09
Октябрь, 5 дней: с 01.10 по 05.10
Итого: 11 + 28 + 31 + 30 + 31 + 30 + 31 + 31 + 30 + 5 = 258
S=P·(1+tT·i)
1) Точные проценты с точным числом дней ссуды (365/365)
S=1 000 000·(1+258365·0.18)=1 127 232.88 руб.
2) Обыкновенные проценты с точным числом дней (365/360)
S=1 000 000·(1+258360·0.18)=1 129 000 руб.
3) Обыкновенные проценты с приближённым числом дней (360/360)
Количество дней между датами: 255
Январь, 10 дней: с 21.01 по 30.01
Февраль, Март, Апрель, Май, Июнь, Июль, Август, Сентябрь по 30 дней
Октябрь, 5 дней: с 01.10 по 05.10
Итого: 10 + 30*8 + 5 = 255
S=1 000 000·(1+255360·0.18)=1 127 500 руб. -
Через d = 180 дней после подписания договора должник уплатит S = 310 тыс.руб. Кредит выдан под i = 16% годовых. Какова первоначальная сумма долга при условии, что временная база равна 365 дням?
P=S(1+tT·i)
Находим современную стоимость P=310 000(1+180365·0.16) = 287 328.59 руб.
Вспомогательные формулы
Привожу еще пару вспомогательных формул, которые могут пригодиться при составлении личного финансового плана. Они выражаются из уже написанных выше. Рассмотрим все на примерах задач.
Задача №1
Дано:
- у вас есть 60 тыс. рублей
- вы хотите приумножить их до 250 тыс. рублей
- у вас есть срок 15 лет
Найти:
под какую процентную ставку нужно вложить деньги?
Расчет:
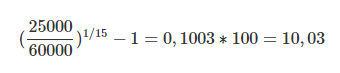
Ответ равен 10,03 процентам
Задача №2
Дано:
- у вас есть 50 тыс. рублей
- вы хотите приумножить их до 1 млн. рублей
- вы уверены, что сможете вложить их под 40% годовых
Найти:
сколько потребуется для этого времени в годах?
Расчет:
Ответ: 8,9 лет.
Что такое сложный процент в инвестициях простыми словами
Знание механизма расчета по депозиту позволяет вкладчикам составить прогноз дохода. Этот расчет доступен при заключении соглашений, выполнении транзакций, перед начислением вознаграждения и капитализацией прибыли.
 Банки пользуются простыми и сложными формулами.
Банки пользуются простыми и сложными формулами.
При этом применяется фиксированная ставка, которая закрепляется договором при размещении депозита, может регулироваться в случаях:
- автоматической пролонгации договора;
- досрочного закрытия.
Плавающий тип может меняться на протяжении действия соглашения.
Изменение ставок в этом случае привязано к таким факторам:
- курсу валют;
- переводу депозита в другую категорию.
При расчете дохода учитывается ряд показателей:
- инвестиционная сумма;
- процентная ставка, ее тип;
- периодичность начислений;
- срок договора.

При использовании простой схемы расчета итог получается в результате таких математических действий. Начальная сумма умножается на годовую ставку и количество дней начисления вознаграждения и делится на количество дней по календарю и на 100.

Зачем инвестировать под сложный процент
При инвестировании денег рекомендуется выбрать оптимальный вариант, который позволит использовать преимущества сложных ставок. Вложению денег всегда предшествует планирование, анализ поставленной задачи. Капитализация прибыли от инвестирования на счет позволяет получить дополнительный доход.
Простой расчет
Эффективной ставкой считается номинальный процент, который начисляется на сумму с капитализацией. Рассчитать доход можно в программе Excel. Для этого следует ввести исходные данные, формулы на базовый депозит, сумму с капитализацией. Действия выполняются автоматически, поэтому для получения корректного результата рекомендуется внимательно ввести информацию.
Формула
Плата за пользование средствами финансовым учреждением начисляется ежемесячно. Если вкладчик не будет снимать эти средства со счета, то они дополнят сумму основного депозита.
Формула сложного процента записывается: S=X*(1+%)n, где
- S — конечная сумма;
- X — начальный вклад;
- % — годовая ставка;
- n — количество периодов.
В результате прибыль добавляется к сумме и дает доход. Сложный расчет может действовать при открытии .

Выбирая программное предложение банка, нужно ориентироваться на итоговый доход в денежном выражении, который получится при размещении средств.
Пример сложного процента на банковском депозите
Удобно и выгодно, когда ваши деньги одномоментно задействованы в разных инструментах. Сразу рекомендую не только у менеджера устно, но и в письменном договоре детально изучить — какой именно процент используется и какие есть нюансы по нему. На некоторых банковских сайтах или в мобильных приложениях есть калькулятор сложных процентов с капитализацией и пополнением. Показываю, как работает эта формула.
- Первоначальный вклад составил 100 тыс. рублей на 1 год с правом пополнения без ограничения суммы под 5% годовых.
- Во втором полугодии вы добавили к вкладу еще 100 тыс. рублей.
- За первую половину вы заработали (100000/100*5%) / 2=2500. Во втором полугодии получили (200000/100*5%) / 2 = 5000. Итого прибыль за год 7500.
- Далее вы можете забрать свои 7500 или добавить их к 200 тыс. или увеличить вклад еще на определенную сумму.
Наиболее выгодно так работать с проверенными инструментами, поэтапно повышая сумму вклада и внося все данные в excel, чтобы не заблудиться.
Как правило, разница на доходе с правом неограниченного пополнения и на обычном способе не превышает 0,5-1% в год, а иногда и вовсе отсутствует.
Ради справедливости нужно рассмотреть и правило, как работает формула расчета простых процентов по кредиту, поскольку ее часто применяют в работе. Простой процент начисляется так: сумма кредита умножается на процентную ставку и поделенная на 365 дней. Для примера: у вас кредит на 100 тыс. рублей под 10% годовых. Если предложен дифференцированный способ, то ежемесячно вам будет начисляться 1000 рублей непосредственно за пользование средствами.

Оплачивая их, через определенный срок можно приступить к погашению самого «тела». Многие банки предлагают аннуитетный платеж, работающий по формуле сложного процента. Это означает, что вы будете оплачивать кредит плюс-минус равными долями. 1000 рублей в месяц за сам кредит и, например, 1000 рублей за само тело. Таким образом, уже на второй месяц проценты будут начисляться на 99 тыс. остатка и с каждым месяцем и платеж по процентам, и выплаты по кредиту будут уменьшаться.
Обратите внимание: сложные проценты по кредиту предлагаются на средних и высоких суммах, в частности, когда оформляете ипотеку или покупаете по договору автомобиль из салона. Хотя есть и аналогичные предложения среди кредитных карт, например, карта Халва, где выплаты подразумеваются равными долями за определенный период и иногда вовсе с минимальными процентами
Узнав способ начисления процента в рабочем инструменте, возможность вносить дополнительно средства или погашать кредит досрочно, важно обратить внимание еще на один аспект — ставку дисконтирования. Это величина, применяемая для пересчета грядущих денежных потоков в общую величину актуальной стоимости. С математической точки зрения, это формула, обратная сложному проценту
С ее помощью оценивается, сколько нужно сейчас инвестировать средств, чтобы, например, через 2 года, получить 100 тысяч. Рассчитывается она по формуле: итоговая сумма (100 тыс. руб) равно как произведение неизвестного на (1+0,1 (10% — средняя ставка банка)), возведенное в квадрат. Далее по правилу пропорции выделите тот самый Х (икс). Фактически, это 82644 рубля
С математической точки зрения, это формула, обратная сложному проценту. С ее помощью оценивается, сколько нужно сейчас инвестировать средств, чтобы, например, через 2 года, получить 100 тысяч. Рассчитывается она по формуле: итоговая сумма (100 тыс. руб) равно как произведение неизвестного на (1+0,1 (10% — средняя ставка банка)), возведенное в квадрат. Далее по правилу пропорции выделите тот самый Х (икс). Фактически, это 82644 рубля.
Учитывайте правило: ставка дисконтирования должна быть выше предложенной доходности.
В итоге подчеркну: сложные проценты в финансовых инструментах только на первый взгляд выглядят сложными, но, если разобраться в их сути, никаких камней преткновения не возникнет, а еще более — вы сможете получить существенную выгоду. Всем желаю только выгодных начислений для инвестиций и минимальных для кредита, если же вы все же решились его оформить.
Профессиональный инвестор с опытом работы 5 лет с разными финансовыми инструментами, ведет свой блог и консультирует вкладчиков. Собственные эффективные методики и информационное сопровождение инвестиций.
Послесловие
В рамках данного обзора, вы узнали что такое капитализация процента, какова формула сложных процентов, а так же увидели пример с расчетом, демонстрирующим разницу в доходе.
Хоть, сложные проценты и могут представлять интерес, всегда важно помнить про здравую логику и то, что у вас своя голова. Во-первых, могут присутствовать различные тонкости (что и когда можно снимать, что происходит если снять деньги раньше, некратные периоды и так далее)
Во-вторых, чрезмерные сложности при расчетах и сравнении, особенно если используются дробные цифры (например, 6,03% в год с ежегодной капитализацией за 10 лет составит примерно 79,6% дохода, а вот 5,96% при ежемесячной капитализации составит 81,2%). Подобные вещи непросто заметить обычному человеку.
В-третьих, капитализация предусматривает автоматическое повторное вложение денег, в то время как простые проценты могут подразумевать возможность использовать доход для иных целей. И так далее.
Формулы расчета
Раз есть сложный, значит, есть и простой процент. Несправедливо, если мы не разберем младшего брата нашего героя.
Простой процент
Простой процент каждый расчетный период (месяц, квартал, год) начисляется только на первоначальную сумму. Никакого эффекта “снежного кома” он не дает. Сумма увеличивается медленно.
Формула расчета:
SN = SП * (1 + % ст * N), где
- SN – сумма в конце периода N;
- SП – первоначальная сумма капитала;
- % ст – процентная ставка (доход);
- N – расчетный период.
Формула справедлива, если речь идет о начислении дохода раз в год. Например, положили на счет 100 000 ₽ под 10 % годовых на 10 лет. В конце срока получите: 100 000 * (1 + 0,1 * 10) = 200 000 ₽.
В реальной жизни понятие простого % применяется, например, в экономических расчетах по банковским вкладам без учета капитализации. В договоре обязательно указывается годовая процентная ставка. Проценты начисляются за каждый день нахождения денег на вкладе. А получать доход вкладчик может ежемесячно, ежеквартально или раз в год.
В этом случае формула примет вид:
SN = SП * (1 + % ст * Д / 365), где
Д – количество полных дней нахождения денег на депозите.
Например:
- Положили на счет 100 000 ₽ под 10 % годовых на 91 день. В конце срока получите: 100 000 * (1 + 0,1 * 91 / 365) = 102 493,15 ₽.
- На 180 дней: 100 000 * (1 + 0,1 * 180 / 365) = 104 931,51 ₽.
- На 2 года (730 дней): 100 000 * (1 + 0,1 * 730 / 365) = 120 000 ₽.
Сложный процент с начислением дохода 1 раз в год
По методу сложных процентов при начислении дохода 1 раз в год будущая сумма определяется по формуле:
SN = SП * (1 + % ст)N
Пример. В банк положили 100 000 ₽ под 10 % годовых на 2 года. Будущая стоимость вклада составит: 100 000 * (1 + 0,1)2 = 121 000 ₽.
Сложный процент с начислением дохода чаще, чем 1 раз в год
Доход может начисляться ежемесячно, ежеквартально или 2 раза в год. Формула меняется:
SN = SN * (1 + % ст / К)N*К, где
К – частота начисления дохода (12, 4 или 2 раза в год).
Пример. В банк положили 100 000 ₽ под 10 % годовых на 2 года с ежемесячным начислением процентов. Будущая стоимость вклада составит: 100 000 * (1 + 0,1/12)24 = 122 039,1 ₽.
Заключение
Используйте силу сложного процента для создания личного капитала. Чем раньше начнете, тем быстрее он сформируется и станет обеспечивать вас и ваших детей. Время и дисциплина – наши помощники.
Поэтому так важно уже в подростковом возрасте объяснять, что и как работает в мире финансов. У молодых людей есть достаточно времени, чтобы обеспечить свою пенсию
Начать можно с небольших, но регулярных сумм, а потом увеличивать размер инвестиций, чтобы быстрее достичь финансовых целей. А вы верите в то, что государство придумает, как вас обеспечить в старости? Или уже начали сами строить свое будущее?