Регрессионный анализ данных в excel

Линейная регрессия в программе Excel

Внизу, в качестве примера, представлена таблица, в которой указана среднесуточная температура воздуха на улице, и количество покупателей магазина за соответствующий рабочий день. Давайте выясним при помощи регрессионного анализа, как именно погодные условия в виде температуры воздуха могут повлиять на посещаемость торгового заведения.

Общее уравнение регрессии линейного вида выглядит следующим образом: У = а0 + а1х1 +…+акхк . В этой формуле Y означает переменную, влияние факторов на которую мы пытаемся изучить. В нашем случае, это количество покупателей. Значение x – это различные факторы, влияющие на переменную. Параметры a являются коэффициентами регрессии. То есть, именно они определяют значимость того или иного фактора. Индекс k обозначает общее количество этих самых факторов.

1. Кликаем по кнопке «Анализ данных». Она размещена во вкладке «Главная» в блоке инструментов «Анализ».

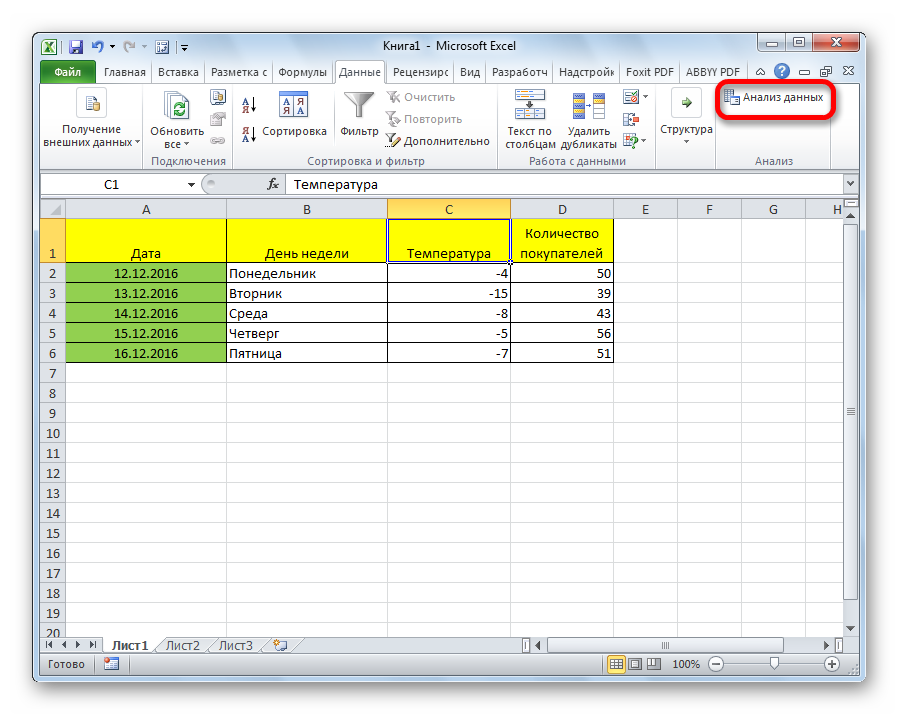
Открывается небольшое окошко. В нём выбираем пункт «Регрессия». Жмем на кнопку «OK».

Открывается окно настроек регрессии. В нём обязательными для заполнения полями являются «Входной интервал Y» и «Входной интервал X». Все остальные настройки можно оставить по умолчанию.

В поле «Входной интервал Y» указываем адрес диапазона ячеек, где расположены переменные данные, влияние факторов на которые мы пытаемся установить. В нашем случае это будут ячейки столбца «Количество покупателей». Адрес можно вписать вручную с клавиатуры, а можно, просто выделить требуемый столбец. Последний вариант намного проще и удобнее.

В поле «Входной интервал X» вводим адрес диапазона ячеек, где находятся данные того фактора, влияние которого на переменную мы хотим установить. Как говорилось выше, нам нужно установить влияние температуры на количество покупателей магазина, а поэтому вводим адрес ячеек в столбце «Температура». Это можно сделать теми же способами, что и в поле «Количество покупателей».

С помощью других настроек можно установить метки, уровень надёжности, константу-ноль, отобразить график нормальной вероятности, и выполнить другие действия. Но, в большинстве случаев, эти настройки изменять не нужно

Единственное на что следует обратить внимание, так это на параметры вывода. По умолчанию вывод результатов анализа осуществляется на другом листе, но переставив переключатель, вы можете установить вывод в указанном диапазоне на том же листе, где расположена таблица с исходными данными, или в отдельной книге, то есть в новом файле

После того, как все настройки установлены, жмем на кнопку «OK».

Линейная регрессия в Excel

Теперь, когда под рукой есть все необходимые виртуальные инструменты для осуществления эконометрических расчетов, можем приступить к решению нашей задачи. Для этого:

• щелкаем по кнопке «Анализ данных»;
• в открывшемся окне нажимаем на кнопку «Регрессия»;
• в появившуюся вкладку вводим диапазон значений для Y (количество уволившихся работников) и для X (их зарплаты);
• подтверждаем свои действия нажатием кнопки «Ok».

В результате программа автоматически заполнит новый лист табличного процессора данными анализа регрессии

Обратите внимание! В Excel есть возможность самостоятельно задать место, которое вы предпочитаете для этой цели. Например, это может быть тот же лист, где находятся значения Y и X, или даже новая книга, специально предназначенная для хранения подобных данных

Недостаток R2{\displaystyle R^{2}} и альтернативные показатели

Основная проблема применения (выборочного) R2{\displaystyle R^{2}} заключается в том, что его значение увеличивается (не уменьшается) от добавления в модель новых переменных, даже если эти переменные никакого отношения к объясняемой переменной не имеют! Поэтому сравнение моделей с разным количеством факторов с помощью коэффициента детерминации, вообще говоря, некорректно. Для этих целей можно использовать альтернативные показатели.

Скорректированный (adjusted) R2{\displaystyle R^{2}}

Для того, чтобы была возможность сравнивать модели с разным числом факторов так, чтобы число регрессоров (факторов) не влияло на статистику R2{\displaystyle R^{2}} обычно используется скорректированный коэффициент детерминации, в котором используются несмещённые оценки дисперсий:

Radj2=1−s2sy2=1−SSres(n−k)SStot(n−1)=1−(1−R2)(n−1)(n−k)⩽R2{\displaystyle R_{adj}^{2}=1-{\frac {s^{2}}{s_{y}^{2}}}=1-{\frac {SS_{res}/(n-k)}{SS_{tot}/(n-1)}}=1-(1-R^{2}){(n-1) \over (n-k)}\leqslant R^{2}}

который даёт штраф за дополнительно включённые факторы, где n — количество наблюдений, а k — количество параметров.

Данный показатель всегда меньше единицы, но теоретически может быть и меньше нуля (только при очень маленьком значении обычного коэффициента детерминации и большом количестве факторов). Поэтому теряется интерпретация показателя как «доли». Тем не менее, применение показателя в сравнении вполне обоснованно.

Для моделей с одинаковой зависимой переменной и одинаковым объёмом выборки сравнение моделей с помощью скорректированного коэффициента детерминации эквивалентно их сравнению с помощью остаточной дисперсии s2=SSres(n−k){\displaystyle s^{2}=SS_{res}/(n-k)} или стандартной ошибки модели s{\displaystyle s}. Разница только в том, что последние критерии чем меньше, тем лучше.

Информационные критерии

AIC — информационный критерий Акаике — применяется исключительно для сравнения моделей. Чем меньше значение, тем лучше. Часто используется для сравнения моделей временных рядов с разным количеством лагов. AIC=2kn+ln⁡SSresn{\displaystyle AIC={2k \over n}+\ln {SS_{res} \over n}}, где k— количество параметров модели.
BIC или SC — байесовский информационный критерий Шварца — используется и интерпретируется аналогично AIC. BIC=kln⁡nn+ln⁡SSresn{\displaystyle BIC={k\ln {n} \over n}+\ln {SS_{res} \over n}}. Даёт больший штраф за включение лишних лагов в модель, чем AIC.

R2{\displaystyle R^{2}}-обобщённый (extended)

В случае отсутствия в линейной множественной МНК регрессии константы свойства коэффициента детерминации могут нарушаться для конкретной реализации. Поэтому модели регрессии со свободным членом и без него нельзя сравнивать по критерию R2{\displaystyle R^{2}}. Эта проблема решается с помощью построения обобщённого коэффициента детерминации Rextended2{\displaystyle R_{extended}^{2}}, который совпадает с исходным для случая МНК регрессии со свободным членом, и для которого выполняются четыре свойства, перечисленные выше. Суть этого метода заключается в рассмотрении проекции единичного вектора на плоскость объясняющих переменных.

Для случая регрессии без свободного члена:
Rextended2=1−Y′∗(I−P(X))∗YY′∗(I−π(X))∗Y{\displaystyle R_{extended}^{2}=1-{Y’*(I-P(X))*Y \over Y’*(I-\pi (X))*Y}},
где X — матрица nxk значений факторов, P(X)=X∗(X′∗X)−1∗X′{\displaystyle P(X)=X*(X’*X)^{-1}*X’} — проектор на плоскость X, π(X)=P(X)∗in∗in′∗P(X)in′∗P(X)∗in{\displaystyle \pi (X)={P(X)*i_{n}*i_{n}’*P(X) \over i_{n}’*P(X)*i_{n}}}, где in{\displaystyle i_{n}} — единичный вектор nx1.

Rextended2{\displaystyle R_{extended}^{2}}с условием небольшой модификации, также подходит для сравнения между собой регрессий, построенных с помощью: МНК, обобщённого метода наименьших квадратов (ОМНК), условного метода наименьших квадратов (УМНК), обобщённо-условного метода наименьших квадратов (ОУМНК).

Пример решения нахождения модели множественной регрессии

Множественная регрессия с двумя переменными

Модель множественной регрессии вида Y = b +b₁X₁ + b₂X₂; 1) Найтинеизвестные b, b₁,b₂ можно, решим систему трехлинейных уравнений с тремя неизвестными b,b₁,b₂: Для решения системы можете воспользоваться решение системы методом Крамера2) Или использовав формулыДля этого строим таблицу вида:

Y	x1	x2	(y-yср)2	(x1-x1ср)2	(x2-x2ср)2	(y-yср)(x1-x1ср)	(y-yср)(x2-x2ср)	(x1-x1ср)(x2-x2ср)

Выборочные дисперсии эмпирических коэффициентов множественной регрессии можно определить следующим образом: Здесь z’_jj — j-тый диагональный элемент матрицы Z-1 =(XTX)-1. Приэтом: где m — количество объясняющихпеременных модели.В частности, для уравнения множественной регрессии

Y = b + b₁X₁ + b₂X₂

с двумя объясняющими переменными используются следующие формулы:Или или,,. Здесьr₁₂ — выборочный коэффициент корреляции между объясняющимипеременными X₁ и X₂; Sb_j — стандартная ошибкакоэффициента регрессии; S — стандартная ошибка множественной регрессии (несмещенная оценка).По аналогии с парной регрессией после определения точечных оценокb_j коэффициентов βj (j=1,2,…,m) теоретического уравнения множественной регрессии могут быть рассчитаны интервальные оценки указанных коэффициентов.

Доверительный интервал, накрывающий с надежностью (1-α) неизвестное значение параметра βj, определяется как

Решение эконометрики в Экселе

Задача 1. Парная регрессия.
Для исходных данных, приведенных ниже, рассчитайте

• коэффициенты линейного регрессионного уравнения
• рассчитайте остаточную дисперсию
• вычислите значения коэффициентов корреляции и детерминации
• рассчитайте коэффициент эластичности
• рассчитайте доверительные границы уравнения регрессии (по уровню 0,95, t=2,44)
• в одной системе координат постройте: уравнение регрессии, экспериментальные точки, доверительные границы уравнения регрессии

Отчет (pdf), Расчеты (xlsx)

Задача 2. Построить требуемое уравнение регрессии. Вычислить коэффициент детерминации, коэффициент эластичности, бета коэффициент и дать их смысловую нагрузку в терминах задачи. Проверить адекватность уравнения с помощью F теста. Найти дисперсии оценок и 95% доверительные интервалы для параметров регрессии. Данные взять из таблицы. Найти прогнозируемое значение объясняемой переменной для некоторого значения объясняющей переменной, не заданной в таблице. Построить уравнение линейной регрессии объема валового выпуска (в млн. руб.) от стоимости основных производственных фондов (млн. руб.).

Отчет (pdf), Расчеты (xlsx)

Задача 3. Множественная регрессия.
Построить требуемое уравнение регрессии. Вычислить коэффициент детерминации, частные коэффициенты эластичности, частные бета коэффициенты и дать их смысловую нагрузку в терминах задачи. Проверить адекватность уравнения с помощью F теста. Найти оценку матрицы ковариаций оценок параметров регрессии и 95% доверительные интервалы для параметров регрессии. Проверить наличие мультиколлинеарности в модели. Данные взять из таблицы.
Построить уравнение линейной регрессии себестоимости единицы товара (в сотнях руб.) от величины энерговооруженности (кВт) и производительности труда (тов/час).

Отчет (pdf), Расчеты (xlsx)

Задача 4. Трендовые модели
Проверить ряд на наличие тренда. Сгладить ряд методом простой скользящей средней $(m = 3)$, экспоненциальным сглаживанием $(\alpha = 0,3; \alpha = 0,8)$. Построить исходный и сглаженные ряды. На основании построенных рядов определить вид трендовой модели. Построить трендовую модель.
Сделать прогноз изучаемого признака на два шага вперед.
87; 77; 75; 74; 69; 66; 62; 61; 59; 57; 57; 52; 50; 48; 46; 43; 43; 41; 38; 35

Отчет (pdf), Расчеты (xlsx)

Задача 5.
По заданным статистическим данным постройте линейную модель множественной регрессии и исследуйте её.

• Постройте линейную модель множественной регрессии.
• Запишите стандартизованное уравнение множественной регрессии. На основе стандартизованных коэффициентов регрессии и средних коэффициентов эластичности ранжировать факторы по степени их влияния на результат.
• Найдите коэффициенты парной, частной и множественной корреляции. Проанализируйте их.
• Найдите скорректированный коэффициент множественной детерминации. Сравните его с нескорректированным (общим) коэффициентом детерминации.
• С помощью F-критерия Фишера оценить статистическую надежность уравнения регрессии и коэффициента детерминации $R^2_{y x_1 x_2}$.
• С помощью частных F-критериев Фишера оценить целесообразность включения в уравнение множественной регрессии фактора $x_1$ после $x_2$ и фактора $x_2$ после $x_1$.
• Составьте уравнение линейной парной регрессии, оставив лишь один значащий фактор.

Отчет (pdf), Расчеты (xlsx)

Задача 6. По данным опроса 15 женщин, находящихся в роддоме, исследовать
зависимость веса новорожденного (у) от среднего числа сигарет (х), выкуриваемых матерью в день, с учетом числа уже имеющихся у матери детей (z).

Может пригодиться: примеры решений по эконометрике, лабораторные по статистике в Excel

Заказать решение задач по эконометрике просто

Оценим уже сегодня

Основные задачи и виды регрессии

Регрессия представляет собой зависимость между заданными переменными, за счет чего можно определить прогноз будущего поведения данных переменных. Переменные — это различные периодические явления, включая и поведение человека. Такой анализ программы Excel применяется для того, чтобы проанализировать воздействие на конкретную зависимую переменную значений одной или некоторым количеством переменных. К примеру, на продажи в магазине влияет несколько факторов, включая ассортимент, цены и место локализации магазина. Благодаря регрессии в Excel можно определять степень влияния каждого из указанных факторов по результатам имеющихся продаж, а после применить полученные данные для прогнозирования продаж на другой месяц или для другого магазина, расположенного рядом.

Обычно регрессия представлена в виде простого уравнения, раскрывающего зависимости и силу связи между двумя группами переменных, где одна группа является зависимой или эндогенной, а другая — независимой или экзогенной. При наличии группы взаимосвязанных показателей зависимая переменная Y определяется исходя из логики рассуждений, а остальные выступают в роли независимых Х-переменных.

Основные задачи построения регрессионной модели заключаются в следующем:

1. Отбор значимых независимых переменных (Х1, Х2, …, Xk).
2. Выбор вида функции.
3. Построение оценок для коэффициентов.
4. Построение доверительных интервалов и функции регрессии.
5. Проверка значимости вычисленных оценок и построенного уравнения регрессии.

Регрессионный анализ бывает нескольких видов:

• парный (1 зависимая и 1 независимая переменные);
• множественный (несколько независимых переменных).

Уравнения регрессии бывает двух видов:

1. Линейные, иллюстрирующие строгую линейную связь между переменными.
2. Нелинейные — уравнения, которые могут включать степени, дроби и тригонометрические функции.

Инструкция построения модели

Чтобы выполнить заданное построение в Excel, необходимо следовать указаниям:

Для дальнейшего вычисления следует использоваться функцию «Линейн ()», указывая Значения Y, Значения Х, Конст и статистику. После этого определите множество точек на линии регрессии с помощью функции «Тенденция» — Значения Y, Значения Х, Новые значения, Конст. При помощи заданных параметров вычислите неизвестное значение коэффициентов, опираясь на заданные условия поставленной задачи.

КОРРЕЛЯЦИОННО-РЕГРЕССИОННЫЙ АНАЛИЗ В MS EXCEL

1. Создайте файл исходных данных в MS Excel (например, таблица 2)

2. Построение корреляционного поля

Для построения корреляционного поля в командной строке выбираем меню Вставка/ Диаграмма . В появившемся диалоговом окне выберите тип диаграммы: Точечная ; вид: Точечная диаграмма , позволяющая сравнить пары значений (Рис. 22).

Рисунок 22 – Выбор типа диаграммы

Рисунок 23– Вид окна при выборе диапазона и рядов Рисунок 25 – Вид окна, шаг 4

2. В контекстном меню выбираем команду Добавить линию тренда.

3. В появившемся диалоговом окне выбираем тип графика (в нашем примере линейная) и параметры уравнения, как показано на рисунке 26.

Нажимаем ОК. Результат представлен на рисунке 27.

Рисунок 27 – Корреляционное поле зависимости производительности труда от фондовооруженности

Аналогично строим корреляционное поле зависимости производительности труда от коэффициента сменности оборудования. (рисунок 28).

от коэффициента сменности оборудования

3. Построение корреляционной матрицы.

Для построения корреляционной матрицы в меню Сервис выбираем Анализ данных.

С помощью инструмента анализа данных Регрессия , помимо результатов регрессионной статистики, дисперсионного анализа и доверительных интервалов, можно получить остатки и графики подбора линии регрессии, остатков и нормальной вероятности. Для этого необходимо проверить доступ к пакету анализа. В главном меню последовательно выберите Сервис/ Надстройки . Установите флажок Пакет анализа (Рисунок 29)

Рисунок 30 – Диалоговое окно Анализ данных

После нажатия ОК в появившемся диалоговом окне указываем входной интервал (в нашем примере А2:D26), группирование (в нашем случае по столбцам) и параметры вывода, как показано на рисунке 31.

Результат расчетов представлен в таблице 4.

Определение и формула

Истинный коэффициент детерминации модели зависимости случайной величины y от факторов x определяется следующим образом:

R2=1−V(y|x)V(y)=1−σ2σy2,{\displaystyle R^{2}=1-{\frac {V(y|x)}{V(y)}}=1-{\frac {\sigma ^{2}}{\sigma _{y}^{2}}},}

где V(y|x)=σ2{\displaystyle V(y|x)=\sigma ^{2}} — условная (по факторам x) дисперсия зависимой переменной (дисперсия случайной ошибки модели).

В данном определении используются истинные параметры, характеризующие распределение случайных величин. Если использовать выборочную оценку значений соответствующих дисперсий, то получим формулу для выборочного коэффициента детерминации (который обычно и подразумевается под коэффициентом детерминации):

R2=1−σ^2σ^y2=1−SSresnSStotn=1−SSresSStot,{\displaystyle R^{2}=1-{\frac {{\hat {\sigma }}^{2}}{{\hat {\sigma }}_{y}^{2}}}=1-{\frac {SS_{res}/n}{SS_{tot}/n}}=1-{\frac {SS_{res}}{SS_{tot}}},}

где SSres=∑i=1nei2=∑i=1n(yi−y^i)2{\displaystyle SS_{res}=\sum _{i=1}^{n}e_{i}^{2}=\sum _{i=1}^{n}(y_{i}-{\hat {y}}_{i})^{2}} — сумма квадратов остатков регрессии, yi,y^i{\displaystyle y_{i},{\hat {y}}_{i}} — фактические и расчётные значения объясняемой переменной.

SStot=∑i=1n(yi−y¯)2=nσ^y2{\displaystyle SS_{tot}=\sum _{i=1}^{n}(y_{i}-{\overline {y}})^{2}=n{\hat {\sigma }}_{y}^{2}} — общая сумма квадратов.

y¯=1n∑i=1nyi{\displaystyle {\bar {y}}={\frac {1}{n}}\sum _{i=1}^{n}y_{i}}

В случае линейной регрессии с константой SStot=SSreg+SSres{\displaystyle SS_{tot}=SS_{reg}+SS_{res}}, где SSreg=∑i=1n(y^i−y¯)2{\displaystyle SS_{reg}=\sum _{i=1}^{n}({\hat {y}}_{i}-{\overline {y}})^{2}} — объяснённая сумма квадратов, поэтому получаем более простое определение в этом случае — коэффициент детерминации — это доля объяснённой суммы квадратов в общей:

R2=SSregSStot{\displaystyle R^{2}={\frac {SS_{reg}}{SS_{tot}}}}

Необходимо подчеркнуть, что эта формула справедлива только для модели с константой, в общем случае необходимо использовать предыдущую формулу.

Интерпретация

1. Коэффициент детерминации для модели с константой принимает значения от 0 до 1. Чем ближе значение коэффициента к 1, тем сильнее зависимость. При оценке регрессионных моделей это интерпретируется как соответствие модели данным. Для приемлемых моделей предполагается, что коэффициент детерминации должен быть хотя бы не меньше 50 % (в этом случае коэффициент множественной корреляции превышает по модулю 70 %). Модели с коэффициентом детерминации выше 80 % можно признать достаточно хорошими (коэффициент корреляции превышает 90 %). Значение коэффициента детерминации 1 означает функциональную зависимость между переменными.
2. При отсутствии статистической связи между объясняемой переменной и факторами, статистика nR2{\displaystyle nR^{2}} для линейной регрессии имеет асимптотическое распределение χ2(k−1){\displaystyle \chi ^{2}(k-1)}, где k−1{\displaystyle k-1} — количество факторов модели (см. тест множителей Лагранжа). В случае линейной регрессии с нормально распределёнными случайными ошибками статистика F=R2(k−1)(1−R2)(n−k){\displaystyle F={\frac {R^{2}/(k-1)}{(1-R^{2})/(n-k)}}} имеет точное (для выборок любого объёма) распределение Фишера F(k−1,n−k){\displaystyle F(k-1,n-k)} (см. F-тест). Информация о распределении этих величин позволяет проверить статистическую значимость регрессионной модели исходя из значения коэффициента детерминации. Фактически в этих тестах проверяется гипотеза о равенстве истинного коэффициента детерминации нулю.
3. В общем случае коэффициент детерминации может быть и отрицательным, это говорит о крайней неадекватности модели: простое среднее приближает лучше.

Использование Пакета анализа EXCEL для построения множественной линейной регрессионной модели

Проведем множественный регрессионный анализ с помощью надстройки MS EXCEL Пакет анализа .

Эффективно использовать надстройку Пакет анализа могут только пользователи знакомые с теорией множественного регрессионного анализа .

В данной статье решены следующие задачи:

• Показано как в MS EXCEL выполнить регрессионный анализ с помощью надстройки Пакет анализа (инструмент Регрессия), т.е. как вызвать надстройку и правильно заполнить входные данные;
• Даны пояснения по разделам отчета, формированного надстройкой;
• Даны комментарии обо всех показателях, рассчитанных надстройкой, и приведены ссылки на соответствующие разделы статей, посвященные простой линейной регрессии .

В надстройке Пакет анализа для построения линейной регрессионной модели (как простой , так и множественной ) имеется специальный инструмент Регрессия .

После выбора этого инструмента откроется окно, в котором требуется заполнить следующие поля (см. файл примера лист Надстройка ):

• Входной интервалY : ссылка на массив значений переменной Y. Ссылку можно указать с заголовком. В этом случае, при выводе результатов надстройка использует Ваш заголовок (для этого в окне требуется установить галочку Метки );
• Входной интервал Х : ссылка на значения переменных Х (нужно указать все столбцы со значениями Х). Ссылку рекомендуется делать на диапазон с заголовками (в окне не забудьте установить галочку Метки );
• Константа-ноль : если галочка установлена, то надстройка подбирает плоскость регрессии с b =0;
• Уровень надежности : Это значение используется для построения доверительных интервалов для наклона и сдвига . Уровень надежности = 1- альфа . Если галочка не установлена или установлена, но уровень значимости = 95%, то надстройка все равно рассчитывает границы доверительных интервалов, причем дублирует их. Если галочка установлена, а уровень надежности отличен от 95%, то рассчитываются 2 доверительных интервала : один для 95%, другой для введенного значения. Для демонстрации вышесказанного введем 90%;
• Выходной интервал: диапазон ячеек, куда будут помещены результаты вычислений. Достаточно указать левую верхнюю ячейку этого диапазона;
• Остатки : будут вычислены остатки модели , т.е. разница между наблюденными и предсказанными значениями Yi для всех наблюдений n;
• Стандартизированные остатки : Вышеуказанные значения остатков будут поделены на значение их стандартного отклонения ;
• График остатков : Для каждой переменной X _j будет построена точечная диаграмма : значения остатков и соответствующее значение Х _ji (при прогнозировании на основании значений 2-х переменных Х будет построено 2 диаграммы (j=1 и 2));
• График подбора: Для каждой переменной X _j будут построены точечные диаграммы с двумя рядами данных : точки данных (X _ji ;Y _i ) и (X _ji ;Y _{iпредсказанное} );
• График нормальной вероятности: Будет построена точечная диаграмма с названием График нормального распределения . По сути — это график значений переменной Y, отсортированных по возрастанию .

В результате вычислений будет заполнен указанный Выходной интервал.

Тот же результат можно получить с помощью формул (см. файл примера лист Надстройка , столбцы I:T).

Результаты вычислений, выполненных надстройкой, полностью совпадают с вычислениями сделанными нами в статье про множественную линейную регрессию с помощью функций ЛИНЕЙН() , ТЕНДЕНЦИЯ() и др. Использование альтернативных формул помогает разобраться с алгоритмом расчета показателей регрессии.

Отчет, сформированный надстройкой, состоит из следующих разделов:

Пакет анализа Excel (программа «Регрессия»)

Расчет параметров уравнения линейной регрессии, проверку их статистической значимости и построения интервальных оценок можно выполнить значительно быстрее автоматически при использовании Пакета анализа Excel (программа «Регрессия»)

Пусть исходные данные примера 2.1 (расходы на питание – личный доход) представлены в Excel.

Выбираем команду Анализ данных→Регрессия.

В диалоговом окне режимаРегрессиязадаются следующие параметры:

Входной интервал У– вводится ссылка на ячейки, содержащие данные по результативному признаку.

Входной интервал Х – вводится ссылка на ячейки, содержащие факторные признаки.

Метки – установите флажок в активное состояние, если выделены и заголовки столбцов.

Константа- ноль – установите флажок в активное состояние, если оцениваете регрессионное уравнение без свободного члена.

При необходимости задаются и другие параметры.

Результаты расчетов с использованием инструмента Регрессия выводятся под общим названием Вывод итоговв виде следующих таблиц.

Результаты работы программы «Регрессия» полностью совпадают с полученными ранее расчетами.

При необходимости выводятся предсказанные значения

Коэффициенты регрессии, их стандартные ошибки и коэффициент детерминации составляют:

a= -1,75; b=0,775;

= 1,65;
=0,143;
= 0,907

Результаты регрессионного анализа принято записывать в виде:

ȳ= -1,75+0,775х ;

= 0,907,

где в скобках указаны стандартные ошибки коэффициентов регрессии.

Статическая значимость коэффициента

F – тесту. ПосколькуF= 0,0124 2

se_y — стандартная ошибка для оценки y;

F — F-статистика, используемая для определения того, является ли наблюдаемая взаимосвязь между зависимой и независимой переменными случайной или нет;

df — степени свободы, используемые для нахождения F-критических значений в статистической таблице (для определения уровня надежности модели нужно сравнить значения в таблице с F-статистикой функции ЛИНЕЙН);

ss_reg — регрессионая сумма квадратов;

ss_resid — остаточная сумма квадратов.

Характеристики выводятся на экран дисплея в виде приведенного ниже массива (таблицы):

Анализ результатов регрессии для R-квадрата

В Excel данные полученные в ходе обработки данных рассматриваемого примера имеют вид:

Прежде всего, следует обратить внимание на значение R-квадрата. Он представляет собой коэффициент детерминации

В данном примере R-квадрат = 0,755 (75,5%), т. е. расчетные параметры модели объясняют зависимость между рассматриваемыми параметрами на 75,5 %. Чем выше значение коэффициента детерминации, тем выбранная модель считается более применимой для конкретной задачи. Считается, что она корректно описывает реальную ситуацию при значении R-квадрата выше 0,8. Если R-квадрата 2 (RI) представляет собой числовую характеристику доли общего разброса и показывает, разброс какой части экспериментальных данных, т.е. значений зависимой переменной соответствует уравнению линейной регрессии. В рассматриваемой задаче эта величина равна 84,8%, т. е. статистические данные с высокой степенью точности описываются полученным УР.

F-статистика, называемая также критерием Фишера, используется для оценки значимости линейной зависимости, опровергая или подтверждая гипотезу о ее существовании.

Значение t-статистики (критерий Стьюдента) помогает оценивать значимость коэффициента при неизвестной либо свободного члена линейной зависимости. Если значение t-критерия > t_кр, то гипотеза о незначимости свободного члена линейного уравнения отвергается.

В рассматриваемой задаче для свободного члена посредством инструментов «Эксель» было получено, что t=169,20903, а p=2,89Е-12, т. е. имеем нулевую вероятность того, что будет отвергнута верная гипотеза о незначимости свободного члена. Для коэффициента при неизвестной t=5,79405, а p=0,001158. Иными словами вероятность того, что будет отвергнута верная гипотеза о незначимости коэффициента при неизвестной, равна 0,12%.

Таким образом, можно утверждать, что полученное уравнение линейной регрессии адекватно.

Изучение результатов и выводы

«Собираем» из округленных данных, представленных выше на листе табличного процессора Excel, уравнение регрессии:

СП = 0,103*СОФ + 0,541*VO – 0,031*VK +0,405*VD +0,691*VZP – 265,844.

В более привычном математическом виде его можно записать, как:

y = 0,103*x1 + 0,541*x2 – 0,031*x3 +0,405*x4 +0,691*x5 – 265,844

Данные для АО «MMM» представлены в таблице:

Подставив их в уравнение регрессии, получают цифру в 64,72 млн американских долларов. Это значит, что акции АО «MMM» не стоит приобретать, так как их стоимость в 70 млн американских долларов достаточно завышена.

Как видим, использование табличного процессора «Эксель» и уравнения регрессии позволило принять обоснованное решение относительно целесообразности вполне конкретной сделки.

Теперь вы знаете, что такое регрессия. Примеры в Excel, рассмотренные выше, помогут вам в решение практических задач из области эконометрики.

Известна тем, что она полезна в разных областях деятельности, включая и такую дисциплину, как эконометрика, где в работе используется данная программная утилита. В основном все действия практических и лабораторных занятий выполняют в Excel, которая существенно облегчает работу, давая подробные объяснения тех или иных действий. Так, один из инструментов анализа «Регрессия» применяется с целью подбора графика для набора наблюдений за счет метода наименьших квадратов. Рассмотрим, что представляет собой данный инструмент программы и в чем заключается его польза для пользователей. Ниже также предоставлена краткая, но понятная инструкция построения регрессионной модели.