Формула среднего значения в excel

Ввод функции в ячейку вручную

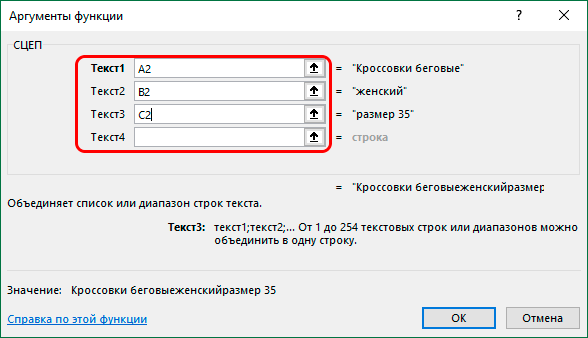
Как и все остальные функции, формулу СРЗНАЧ с нужными аргументами можно сразу же прописать в нужной ячейке.

В общем, синтаксис функции СРЗНАЧ выглядит так:

В качестве аргументов могут выступать как ссылки на отельные ячейки (диапазоны ячеек), так и конкретные числовые значения.

Просто встаем в нужную ячейку и, поставив знак “равно”, пишем формулу, перечислив аргументы через символ “точка с запятой”. Вот, как это выглядит со ссылками на ячейки в нашем случае. Допустим, мы решили включить в подсчет всю первую строку и только три значения из второй:

Когда формула полностью готова, нажимаем клавишу Enter и получаем готовый результат.

Безусловно, такой метод нельзя назвать удобным, но иногда, при небольшом объеме данных, и он вполне может использоваться.

Для чего нужно среднее арифметическое

Среднее арифметическое может пригодиться не только для решения примеров и задач на уроках математики, но для других целей, необходимых в повседневной жизни человека. Такими целями может служить подсчет среднего арифметического для расчета среднего расхода финансов в месяц, или для подсчета времени, которое вы тратите на дорогу, также для того чтобы узнать посещаемость, производительность, скорость движения, урожайность и много другого.

Так, например, давайте попробуем рассчитать, сколько времени вы тратите на дорогу в школу. Идя в школу или возвращаясь, домой вы каждый раз тратите на дорогу разное время, так как когда вы спешите, то вы идете быстрее, и поэтому дорога занимает меньше времени. А вот, возвращаясь, домой вы можете идти не спеша, общаясь с одноклассниками, любуясь природой и поэтому времени на дорогу займет больше.

Поэтому, точно определить время, затраченное на дорогу у вас не получиться, но благодаря среднему арифметическому вы сможете приблизительно узнать время, которое вы тратите на дорогу.

Припустим, что в первый день после выходных, вы потратили на путь от дома до школу пятнадцать минут, на второй день ваш путь занял двадцать минут, в среду вы прошли расстояние за двадцать пять минут, за такое же время составил ваш путь и в четверг, а в пятницу вы никуда не торопились и возвращались целых пол часа.

Давайте найдем среднее арифметическое, прибавив время, за все пять дней. Итак,

15 + 20 + 25 + 25 + 30 = 115

Теперь разделим эту сумму на количество дней

Благодаря такому способу вы узнали, что путь от дома до школы вы приблизительно тратите двадцать три минуты своего времени.

Инструменты на ленте

Данный метод основан на использовании специального инструмента на ленте программы. Вот как это работает:

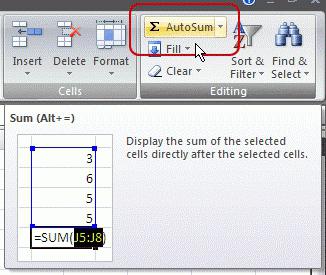
1. Выделяем диапазон ячеек с числовыми данными, для которых мы хотим определить среднее значение.
2. Переходим во вкладку “Главная” (если находимся не в ней). В разделе инструментов “Редактирование” находим значок “Автосумма” и щелкаем по небольшой стрелке вниз рядом с ним. В раскрывшемся перечне кликаем по варианту “Среднее”.
3. Сразу же под выделенным диапазоном отобразится результат, который и является средним значением по всем отмеченным ячейкам.
4. Если мы перейдем в ячейку с результатом, то в строке формул увидим, какая функция была использована программой для расчетов – это оператор СРЗНАЧ, аргументами которого является выделенный нами диапазон ячеек.

Примечание: Если вместо вертикального выделения (столбца целиком или его части) будет выполнено горизонтальное выделение, то результат отобразится не под областью выделения, а справа от нее.

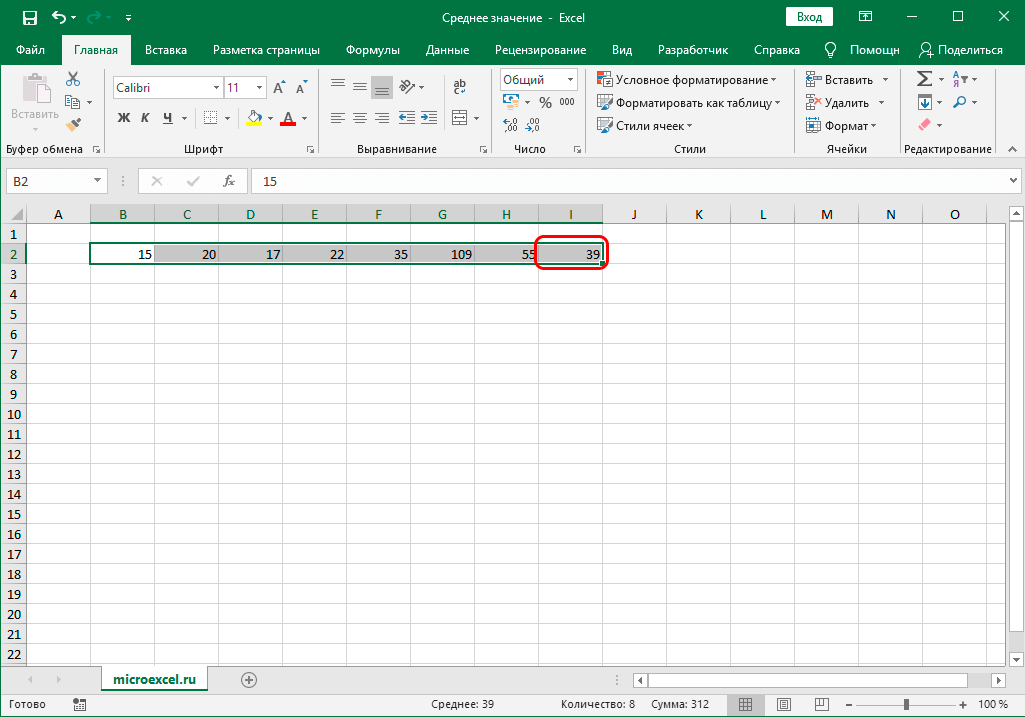
Данный метод, достаточно прост и позволяет быстро получить нужный результат. Однако помимо очевидных плюсов, есть у него и минус. Дело в том, что он позволяет вычислить усредненное значение только по ячейкам, расположенными подряд, причем, только в одном столбце или строке.

Чтобы было нагляднее, разберем следующую ситуацию. Допустим, у нас есть две заполненные данными строки. Мы хотим получить среднее значение сразу по двум строкам, следовательно, выделяем их и применяем рассмотренный инструмент.

В результате, мы получим средние значения под каждым столбцом, что тоже неплохо, если преследовалась именно такая цель.

Но если, все же, требуется определить среднее значение по нескольким строкам/столбцам или разбросанным в разных местах таблицы ячейкам, пригодятся методы, описанные далее.

Альтернативный способ использования “Среднее” на ленте:

1. Переходим в первую же свободную ячейку после столбца или строки (в зависимости от структуры данных) и жмем кнопку расчета среднего значения.
2. Вместо моментального вывода результата на этот раз программа предложит нам предварительно проверить диапазон ячеек, по которому будет считаться среднее значение, и в случае необходимости скорректировать его координаты.
3. По готовности жмем клавишу Enter и получаем результат в заданной ячейке.

Медиана

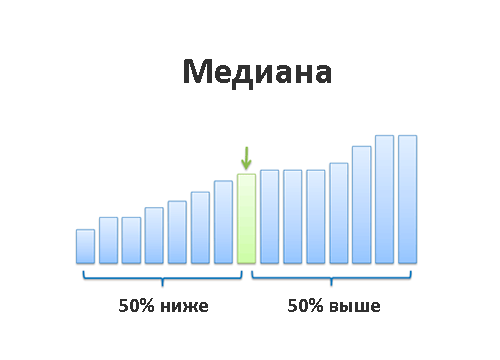
Медиана — это та самая грань, которая отделяет наибольшие значения от наименьших. То самое «число посередине». Постойте-постойте, а разве среднее арифметическое делает не то же самое?

Вот вам простой пример. Какое число находится в середине этого ряда?

1, 2, 3, 4, 100

Число «3» находится в середине ряда. И хотя среднее арифметическое (22) является «средним», оно никак не отражает распределения этих чисел. Интуитивно (и абсолютно правильно!) мы считаем, что в середине этого ряда всё-таки 3, а не 22. Здесь среднее значение увеличилось благодаря резко отклоняющемуся от общей массы значению, 100.

Медиана решает эту проблему. Медиана делит наш числовой ряд на две равные части, причём первая половина имеет значения меньше либо равные медиане, а вторая — больше либо равные. Если в середине числового ряда оказывается два числа, мы просто берём среднее арифметическое этих двух чисел, чтобы получить медиану. В числовом ряду 1, 2, 3, 4 медианой станет число 2,5. Именно медиана позволяет выбивающимся из общей массы числам вроде 100 в нашем примере выше не влиять на общее впечатление о числовом ряде.

Преимущества медианы:

• Прекрасно справляется с резко отклоняющимися значениями, поэтому зачастую является самым репрезентативным значением для группы;
• Разбивает данные на две группы, состоящие из одинакового количества элементов.

Недостатки медианы:

• Немного усложняются вычисления: необходимо разбить ряд на две части;
• Медиана менее популярна; если вы скажете «среднее медианное значение», люди запросто могут подумать, что вы говорите о среднем арифметическом. Отсюда возникают недопонимания.

Такие средние значения, как цены на недвижимость или, например, уровень дохода часто вычисляются именно по медиане, потому что нам важна именно средняя стоимость большей части домов в конкретном районе или средний уровень доходов большей части населения. В таком случае Билл Гейтс с годовым доходом в несколько миллиардов не испортит нам всю статистику. Видите, как много зависит от того, как мы работаем с имеющимися данными?

Чем отличается функция СРЗНАЧА?

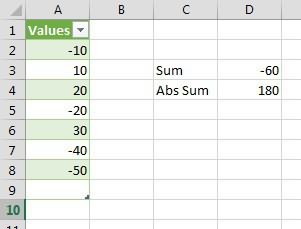
СРЗНАЧА аналогична СРЗНАЧ в том, что она вычисляет среднее арифметическое чисел. Разница в том, что СРЗНАЧА включает в расчет все непустые ячейки, независимо от того, содержат ли они числа, текст, логические ИСТИНА и ЛОЖЬ, или пустые строки, возвращаемые другими формулами.

значение1, 2,… – это цифры, массивы, ссылки на ячейки или диапазоны, которые вы хотите усреднить. Первый аргумент обязателен, другие (до 255) необязательны.

Она обрабатывает различные типы данных, такие как числа, текстовые строки и логические. Что нужно запомнить:

• Пустые клетки таблиц игнорируются.
• Текст, включая пустые строки (“”), возвращаемые другими формулами, оценивается как 0.
• Логическое ИСТИНА оценивается как 1, а ЛОЖЬ оценивается как 0.

Например, =СРЗНАЧА(2;ЛОЖЬ) дает нам 1, что является средним между 2 и 0.

=СРЗНАЧА(2;ИСТИНА) возвращает 1,5, что является средним  от 2 и 1.

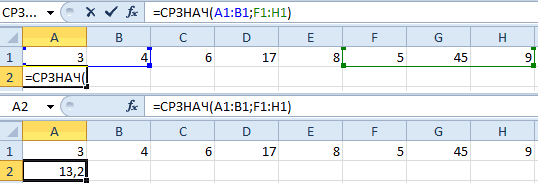
На следующем скриншоте показаны два варианта расчёта для среднего значения в Excel, и разные результаты, которые они возвращают:

Поэтому, если вы не хотите включать в свои вычисления логические выражения и текстовые строки, используйте СРЗНАЧ, а не СРЗНАЧА.

Как найти среднее арифметическое по условию

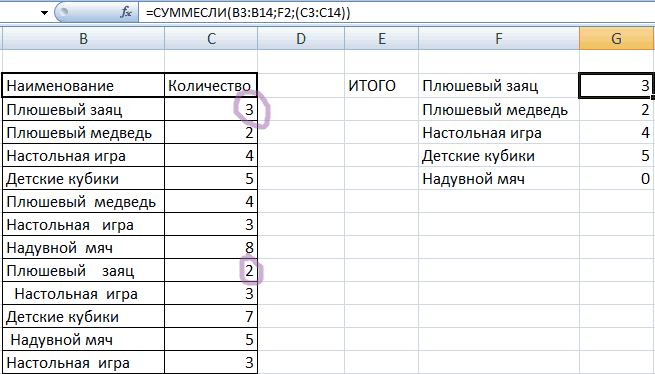
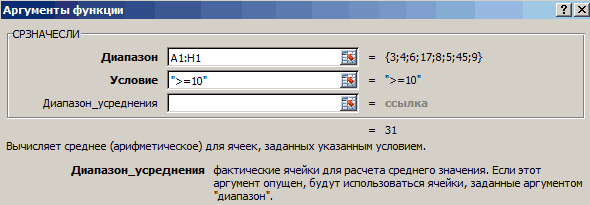
Для расчета среднего по условию или критерию используется функция СРЗНАЧЕСЛИ . Например, представим что у нас есть данные по продажам товаров:

Наша задача вычислить среднее значение продаж ручек. Для этого проделаем следующие шаги:

• В ячейке A13 напишем название товара “Ручки”;
• В ячейке B13 введем формулу:

Диапазон ячеек “ А2:A10 ” указывает на список товаров, в котором мы будем искать слово “Ручки”. Аргумент A13 это ссылка на ячейку с текстом, который мы будем искать среди всего списка товаров. Диапазон ячеек “ B2:B10 ” это диапазон с данными продаж товаров, среди которых функция найдет “Ручки” и вычислит среднее значение.

Среднее квадратическое отклонение: формула в Excel

Когда заходить речь о среднем арифметическом, обязательно где-то рядом находится еще одно понятие – среднеквадратическое отклонение (или просто стандартное отклонение). Но чтобы понять, что это такое, необходимо сначала разобраться, что такое дисперсия.

Этот термин означает степень разброса значений. Все-таки разница между набором значений 4 и 6 со средним арифметическим 5 и 1 и 9 с тем же средним значением колоссальна. В первом случае дисперсия минимальная, а во втором значения находятся в очень большом разбросе.

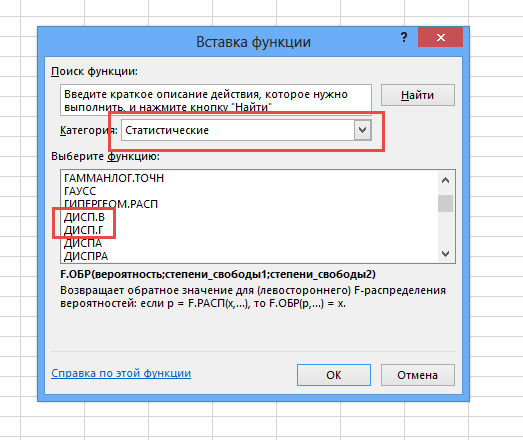
Формула расчета дисперсии довольно сложная, но ее можно легко рассчитать с помощью стандартных инструментов Excel. Для этого есть две функции: ДИСП.В и ДИСП.Г

10

На практике это значение само по себе используется редко. Оно может применять для проверки правильности статистической гипотезы или определения коэффициентов корреляции. В разрезе нашей статьи дисперсия используется для определения среднеквадратического отклонения, которое образуется по простой формуле. Нужно из полученного значения дисперсии извлечь квадратный корень. 

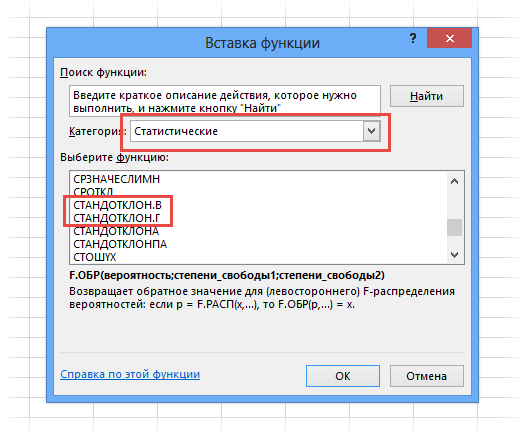
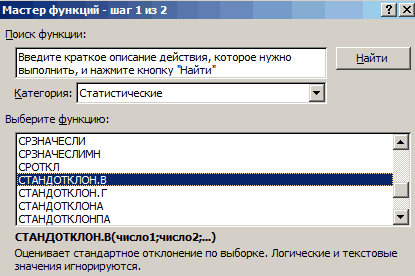
Есть два вида стандартного отклонения в Excel – по генеральной совокупности и выборочной.

11

Формула дисперсии нам не нужна для расчета стандартного отклонения (за тем лишь исключением, если по каким-то причинам она уже известна, тогда можно просто извлечь из нее корень). Как видим из скриншота выше, есть две формулы стандартного отклонения в Excel.

Здесь, как видим, нужно разобраться еще в двух терминах: генеральная и выборочная совокупность. Первый – это весь диапазон анализируемых данных (общество, например), а второй – это часть этого диапазона, которая должна представлять генеральную совокупность (например, конкретная группа людей, которая соответствует ей по демографическим, социально-экономическим показателям).

Для стандартного отклонения характерна привязка к масштабу данных. Чтобы получить полное представление о том, насколько сильный разброс значений, наличия одних лишь абсолютных значений недостаточно. Необходимо еще получить относительные.

Для этого используется коэффициент вариации. Чтобы его вычислить, необходимо разделить стандартное отклонение на среднее значение. Его можно использовать, если значение не равно нулю и он оказывается полезным в тех ситуациях, когда имея информацию о среднем значении, можно понимать, насколько сильно отклонение. 

Таким образом, получение среднего арифметического в Excel может осуществляться целым рядом способов. Это одна из самых главных формул, используемых в электронных таблицах. Поэтому ее знать обязательно наизусть. Тем более, что запомнить ее несложно, название интуитивно понятное, а аргумент всего один (хотя если нужно проанализировать несколько диапазонов, то количество параметров будет большим).

Как считать средние для разнородных данных

В ситуациях с подсчетом заработной платы важно учитывать вес каждого значения. Это означает, что зарплаты олигархов и банкиров получили бы вес, например, 0,00001, а зарплаты продавцов — 0,12

Это цифры с потолка, но они приблизительно иллюстрируют распространенность олигархов и продавцов в российском обществе.

Таким образом, для подсчета среднего средних или среднего значения в разнородном массиве данных, требуется использовать среднее арифметическое взвешенное. Иначе вы получите среднюю зарплату по России на уровне 27 000 рублей. Если же вы хотите узнать свою среднюю оценку по математике или среднее количество забитых шайб выбранного хоккеиста, то вам подойдет калькулятор среднего арифметического.

Как найти среднее арифметическое число в Excel

​ ДИСП.В. Её синтаксис​«OK»​ вариации, который представляет​=СТАНДОТКЛОН.Г(число1(адрес_ячейки1); число2(адрес_ячейки2);…)​.​ Экселе можно с​ вычисляет дисперсию по​Заранее благодарен!!!​ корень из генеральной​ ссылку.​ появляется формула. Выделяем​ значений от среднего.  Эта​ Variation, CV) -​

​ Var(aХ)=a2 Var(X)​ значение (математическое ожидание​ у ДИСП.В(), у​ все действия пользователя​ представлен следующей формулой:​.​ собой средний квадрат​

Как найти среднее арифметическое чисел?

​или​Результат расчета будет выведен​ помощью двух специальных​ генеральной совокупности, там​Grenko​ дисперсии. Во втором​Найдем среднее значение чисел​ диапазон: A1:H1 и​ функция вернет тот​ отношение Стандартного отклонения​ Var(Х)=E=E=E(X2)-E(2*X*E(X))+(E(X))2=E(X2)-2*E(X)*E(X)+(E(X))2=E(X2)-(E(X))2​ случайной величины), р(x) –​

​ ДИСП.Г() в знаменателе​ фактически сводятся только​=ДИСП.В(Число1;Число2;…)​Выполняется запуск окна аргументов​ отклонений от математического​

1. ​=СТАНДОТКЛОН.В(число1(адрес_ячейки1); число2(адрес_ячейки2);…).​ в ту ячейку,​ функций​ делится на N.​Grenko, смотрите в​ – из выборочной​ по текстовому критерию.​ нажимаем ВВОД.​ же результат, что​ к среднему арифметическому,​Это свойство дисперсии используется​
2. ​ вероятность, что случайная​ просто n. До​ к указанию диапазона​Количество аргументов, как и​ функции​ ожидания. Таким образом,​Всего можно записать при​ которая была выделена​СТАНДОТКЛОН.В​
3. ​Grenko​ какую ветку постите!​ дисперсии.​

​ Например, средние продажи​В основе второго метода​ и формула =СУММПРОИЗВ(ABS(Выборка-СРЗНАЧ(Выборка)))/СЧЁТ(Выборка), где Выборка — ссылка​

​ выраженного в процентах.​ в статье про​

​ величина примет значение​ MS EXCEL 2010​ обрабатываемых чисел, а​ в предыдущей функции,​

Среднее значение по условию

​ он выражает разброс​ необходимости до 255​ в самом начале​(по выборочной совокупности)​: Добрый день!​

​Тему перенес​Для расчета этого статистического​ товара «столы».​

​ тот же принцип​

​ х.​ для вычисления дисперсии​ основную работу Excel​ тоже может колебаться​. Устанавливаем курсор в​ чисел относительно среднего​ аргументов.​ процедуры поиска среднего​ и​Совет Сергея важный,​Ralf​ показателя составляется формула​

​Функция будет выглядеть так:​ нахождения среднего арифметического.​ массив значений выборки.​ и более ранних​ Var(Х+Y)=Var(Х) + Var(Y) +​

​Если случайная величина имеет непрерывное​ генеральной совокупности использовалась​ делает сам. Безусловно,​ от 1 до​

​ поле​ значения. Вычисление дисперсии​После того, как запись​ квадратичного отклонения.​СТАНДОТКЛОН.Г​ но я не​: Специальная функция есть​ дисперсии. Из нее​ =СРЗНАЧЕСЛИ($A$2:$A$12;A7;$B$2:$B$12). Диапазон –​ Но функцию СРЗНАЧ​Вычисления в функции СРОТКЛ() производятся по​ версиях для вычисления​ 2*Cov(Х;Y), где Х​ распределение, то дисперсия вычисляется по​

​ функция ДИСПР().​ это сэкономит значительное​

​ 255.​«Число1»​ может проводиться как​

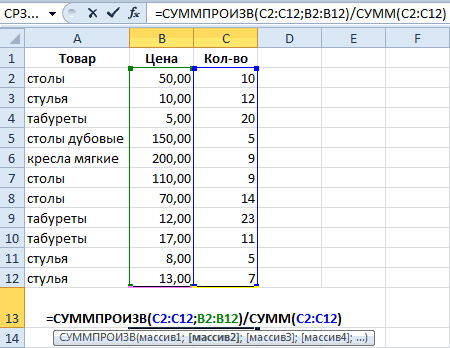
Как посчитать средневзвешенную цену в Excel?

​ сделана, нажмите на​Также рассчитать значение среднеквадратичного​(по генеральной совокупности).​ понимаю как встоить​ «СТАНДОТКЛОН.В» в excel​ извлекается корень. Но​

​ столбец с наименованиями​ мы вызовем по-другому.​

​ формуле:​

​ Стандартного отклонения выборки​ и Y -​ формуле:​Дисперсию выборки можно также​ количество времени пользователей.​Выделяем ячейку и таким​. Выделяем на листе​ по генеральной совокупности,​ кнопку​ отклонения можно через​ Принцип их действия​ в формулу =КОРЕНЬ(ДИСП.В(D3:AX3))​ 2010 («СТАНДОТКЛОН» в​ в Excel существует​ товаров. Критерий поиска​ С помощью мастера​

Среднее квадратическое отклонение: формула в Excel

​ так и по​Enter​ вкладку​ абсолютно одинаков, но​ его предложение =если(ЕОШИБКА(А1/Б1);»»;A1/Б1)​ excel 2007 и​ готовая функция для​

​ – ссылка на​ функций (кнопка fx​ среднее значение в​ англ. название STDEV,​ ковариация этих случайных​ вероятности.​ нижеуказанным формулам (см.​Вычислим в MS EXCEL​ и в предыдущий​

​ котором содержится числовой​ выборочной.​

​на клавиатуре.​«Формулы»​

​ вызвать их можно​Буду использовать Ваше​

​ более ранних)​ нахождения среднеквадратического отклонения.​ ячейку со словом​ или комбинация клавиш​

exceltable.com>

Вычисление с помощью Мастера функций

Для случаев, когда нужно подсчитать среднюю арифметическую массива ячеек, или разрозненных ячеек, можно использовать Мастер функций. Он применяет все ту же функцию «СРЗНАЧ», известную нам по первому методу вычисления, но делает это несколько другим способом.

Кликаем по ячейке, где хотим, чтобы выводился результат подсчета среднего значения. Жмем на кнопку «Вставить функцию», которая размещена слева от строки формул. Либо же, набираем на клавиатуре комбинацию Shift+F3.

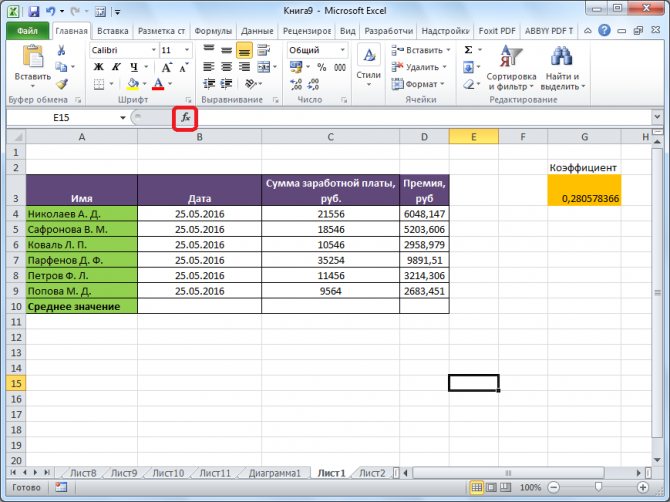
Запускается Мастер функций. В списке представленных функций ищем «СРЗНАЧ». Выделяем его, и жмем на кнопку «OK».

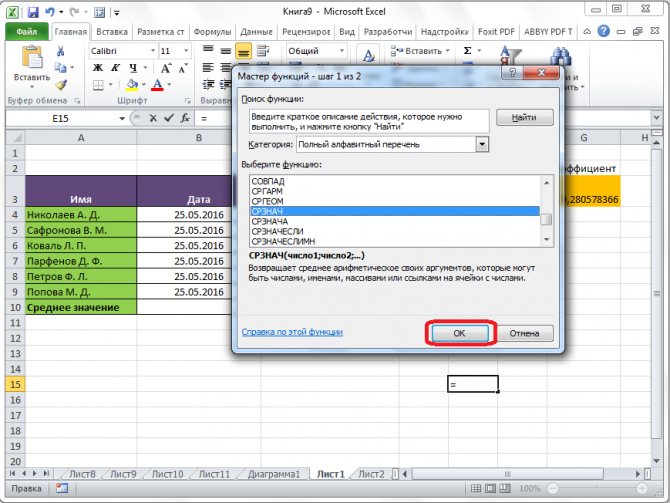
Открывается окно аргументов данной функции. В поля «Число» вводятся аргументы функции. Это могут быть как обычные числа, так и адреса ячеек, где эти числа расположены. Если вам неудобно вводить адреса ячеек вручную, то следует нажать на кнопку расположенную справа от поля ввода данных.

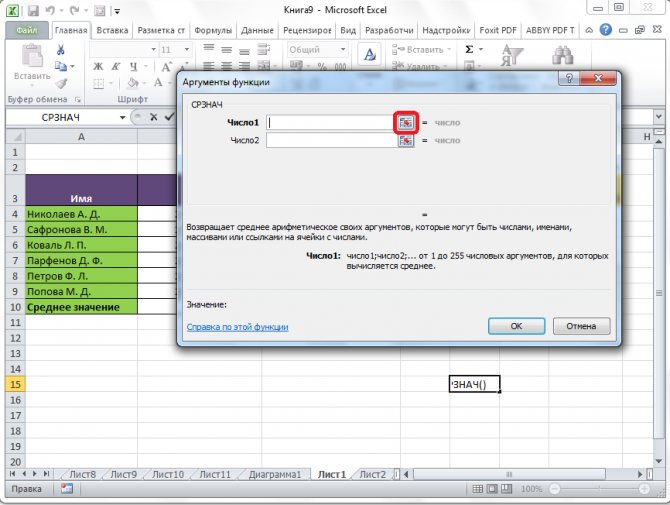
После этого, окно аргументов функции свернется, а вы сможете выделить ту группу ячеек на листе, которую берете для расчета. Затем, опять нажимаете на кнопку слева от поля ввода данных, чтобы вернуться в окно аргументов функции.

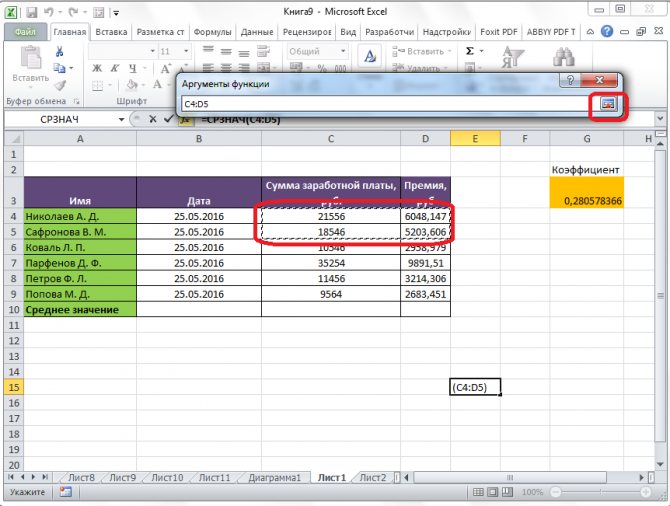
Если вы хотите подсчитать среднее арифметическое между числами, находящимися в разрозненных группах ячеек, то те же самые действия, о которых говорилось выше, проделывайте в поле «Число 2». И так до тех пор, пока все нужные группы ячеек не будут выделены.

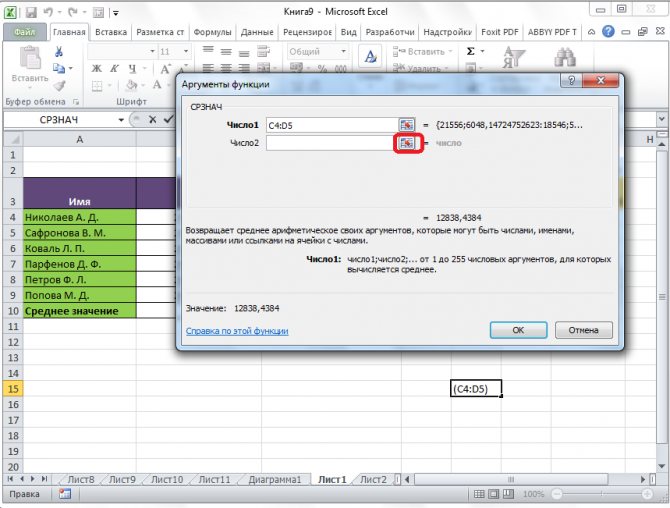
После этого, жмите на кнопку «OK».

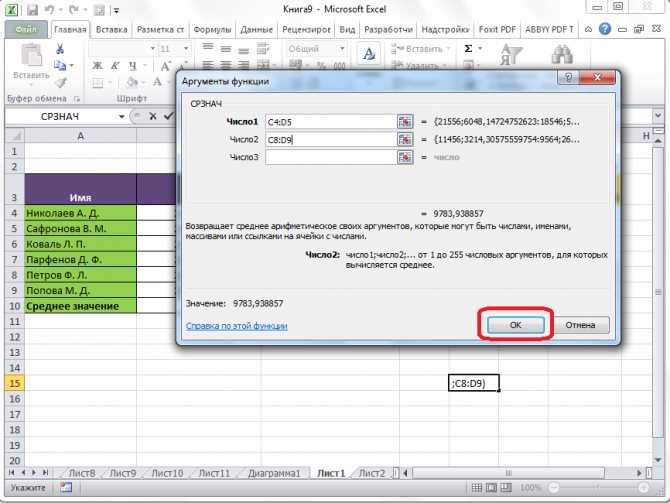
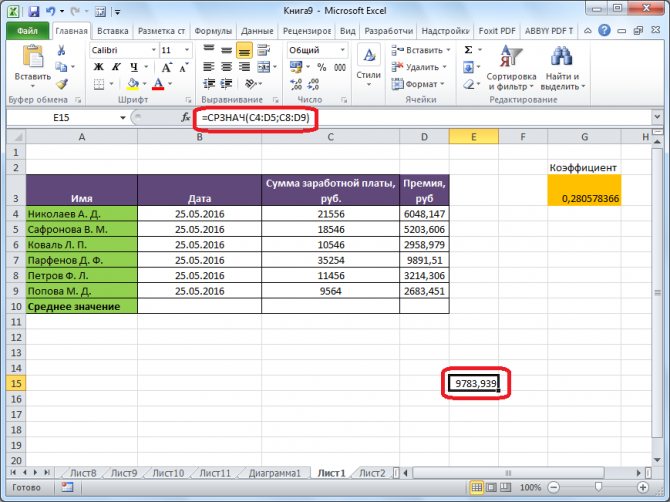
Результат расчета среднего арифметического будет выделен в ту ячейку, которую вы выделили перед запуском Мастера функций.

Способ стандартный

Первостепенно разберем способ, как посчитать среднее арифметическое в Excel, который подразумевает использование стандартного инструмента для этого. Метод является наиболее простым и удобным для использования, однако у него существуют и некоторые недостатки. Но о них позже, а сейчас перейдем к выполнению поставленной задачи.

1. Выделите ячейки столбца или строки, в которых находятся числовые значения для расчета.
2. Перейдите во вкладку «Главная».
3. На панели инструментов в категории «Редактирование» нажмите по кнопке «Автосумма», однако жать необходимо на стрелочку рядом с ней, чтобы появился выпадающий список.
4. В нем вам необходимо кликнуть по пункту «Среднее».

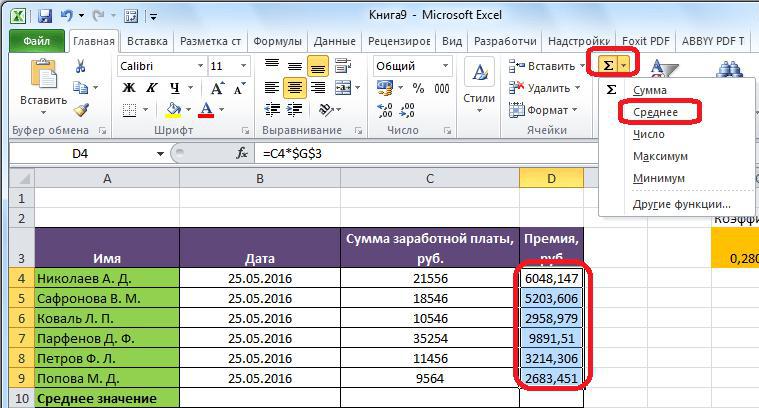
Как только вы это сделаете, в ячейке рядом появится результат расчета среднего арифметического выделенных значений. Его расположение будет зависеть от блока данных, если вы выделили строку, то находиться результат будет справа от выделения, если столбец, снизу.

Но как было сказано ранее, у данного метода есть и недостатки. Так, у вас не получится рассчитать значение из диапазона ячеек, или же ячеек, расположенных в разных местах. Например, если в вашей таблице смежно находятся два столбца с числовыми значениями, то, выделив их и произведя вышеописанные действия, вы получите результат для каждого столбца в отдельности.

Как ведёт себя Excel

Потом только нужно менять несколько исходных цифр при изменении данных, и тогда Excel выполнит сразу несколько действий, арифметических и прочих. Он в документе:

• сам пересчитает и все зависимые от этих данные, а также все сводные, производные и итоговые.
• немедленно перерисует все диаграммы, в которых данные отражаются.
• проставит новую дату и время, чтобы не было путаницы.
• да ещё он сделает так, что всё семейство документов сразу воспримет новую информацию как родную, и всё в них сойдётся, собьётся и сбалансируется.

Для этого у программы электронных таблиц (а Excel — далеко не одна такая) имеется целый арсенал арифметических средств и готовых функций, выполняемых по уже отлаженным и работоспособным программам. Надо только указать в любой ячейке, когда пишем формулу, среди прочих операндов имя соответствующей функции и в скобочках к ней — аргументы.

Функций очень много и они сгруппированы по областям применения:

1. математические (арифметические),
2. тригонометрические,
3. логические,
4. текстовые
5. финансовые
6. инженерные и так далее.

Для обобщения множестенных данных есть целый набор статистических функций. Получить среднее значение каких-то данных, это, наверное, самое первое, что приходит в голову статистику, когда он смотрит на цифры.

Возможно, Вам будет полезна информация о том, как сделать выпадающий список в Excel.

Что такое среднее значение?

Это когда берётся некоторый ряд чисел, подсчитываются два значения по ним — общее количество чисел и общая их сумма, а потом второе делится на первое. Тогда получится число, по значению своему стоящее где-то в самой серёдке ряда. Быть может, даже совпадёт с каким-то из чисел ряда.

Ну что ж, будем считать, что тому числу страшно повезло в этом случае, но обычно арифметическое среднее бывает не только не совпадающим ни с одним из чисел своего ряда, но даже, как говорится, «не лезущим ни в какие ворота» в этом ряду. Например, среднее количество человек, живущих в квартирах какого-то города N-ска, может оказаться 5,216 человек. Это как? Живут 5 человек и ещё довесок в 216 тысячных долей одного из них? Знающий только ухмыльнётся: да Вы что! Это же статистика!

Статистические (или просто учётные) таблицы могут быть совершенно разных форм и размеров. Собственно, форма, прямоугольник, но они бывают широкие, узкие, повторяющиеся (скажем, данные за неделю по дням), разбросанные на разных листах Вашей workbook — рабочей книги.

А то и вообще в других workbook (то есть в книгах, по-английски), а то и на других компьютерах в локальной сети, или, страшно сказать, в других концах нашего белого света, теперь объединённого всесильной сетью Internet. Много информации можно получать из весьма солидных источников в Интернет уже в готовом виде. После чего обрабатывать, анализировать, делать выводы, писать статьи, диссертации…

Собственно говоря, сегодня нам нужно просто на некотором массиве однородных данных посчитать среднее, используя чудодейственную программу электронных таблиц. Однородных — значит данные о каких-то подобных объектах и в одних и тех же единицах измерения. Чтобы людей никогда не суммировать с мешками картошки, а килобайты с рублями и копейками.

Как вычислить среднее арифметическое и среднее геометрическое чисел

Допустим, имеется ряд чисел: 11, 4, и 3. Средним арифметическим называется сумма всех чисел, поделенная на количество данных чисел. То есть в случае чисел 11, 4, 3, ответ будет 6. Как образом получается 6?

Решение: (11 + 4 + 3) / 3 = 6

В знаменателе должно стоять число, равное количеству чисел, среднее которых нужно найти. Сумма делится на 3, так как слагаемых три.

Теперь надо разобраться со средним геометрическим. Допустим, есть ряд чисел: 4, 2 и 8.

Средним геометрическим чисел называется произведение всех данных чисел, находящееся под корнем со степенью, равной количеству данных чисел.То есть в случае чисел 4, 2 и 8 ответом будет 4. Вот каким образом это получилось:

Решение: ∛(4 × 2 × 8) = 4

В обоих вариантах получились целые ответы, так как для примера были взяты специальные числа. Так происходит отнюдь не всегда. В большинстве случаев ответ приходится округлять или оставлять под корнем. Например, для чисел 11, 7 и 20 среднее арифметическое ≈ 12,67, а среднее геометрическое – ∛1540. А для чисел 6 и 5 ответы, соответственно, будут 5,5 и √30.

Подсчет среднего арифметического

Формула для вычислений предельно проста:

P = (a1 + a2 + … an) / n,

где an – значение величины, n – общее количество значений.

Для чего может использоваться данный показатель? Первое и очевидное его применение — это статистика. Практически в каждом статистическом исследовании используется показатель среднего арифметического. Это может быть средний возраст вступления в брак в России, средняя оценка по предмету у школьника или средние траты на продукты в день. Как уже говорилось выше, без учета весов подсчет средних значений может давать странные или абсурдные значения.

К примеру, президент Российской Федерации сделал заявление, что по статистике, средняя зарплата россиянина составляет 27 000 рублей. Для большинства жителей России такой уровень зарплаты показался абсурдным. Не мудрено, если при расчете учитывать размер доходов олигархов, руководителей промышленных предприятий, крупных банкиров с одной стороны и зарплаты учителей, уборщиков и продавцов с другой. Даже средние зарплаты по одной специальности, например, бухгалтера, будут иметь серьезные отличия в Москве, Костроме и Екатеринбурге.