Проценты

Как считать проценты в excel?

Если у вас под рукой имеется компьютер или ноутбук с операционной системой Windows, вам не составит большого труда подсчитать процент от необходимой суммы. Приведем для этого простой пример.

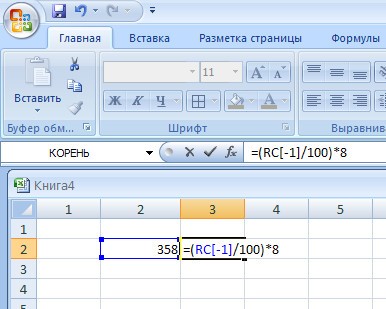
Нам необходимо найти 8% от 358.

1. Открываем Excel.
2. Находим свободную строку.
3. Вводим данные.
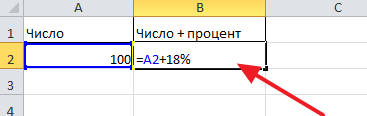
4. Ставим знак «=» и делаем подсчет.
5. Получаем 28,64.

Аналогично к подсчетам на калькуляторе, вы можете ввести в Excel знак %, и это тоже будет правильно.

Иногда нам необходимо узнать процентный показатель от суммы.

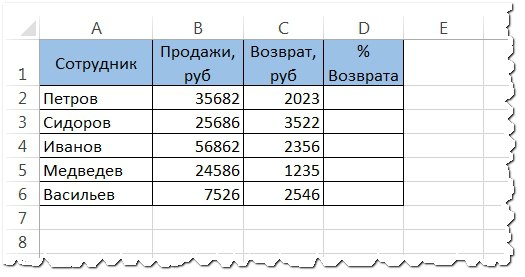
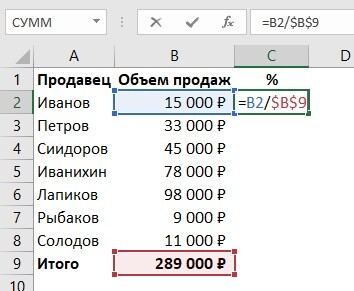
1. К примеру, у нас есть список сотрудников и сумма, на которую они произвели продаж. Помимо этого, известна сумма возвратов. По этим данным мы рассчитываем процент возвратов по товарам.
2. Просчитаем процент для первого показателя в списке — процент возвратов некоего Петрова.
3. Для начала составляем пропорцию, где 100% — это 35682(сумма продаж Петрова). х% — 2023 (сумма возвратов Петрова).
4. Решаем эту пропорцию по формуле, известной нам со школы.
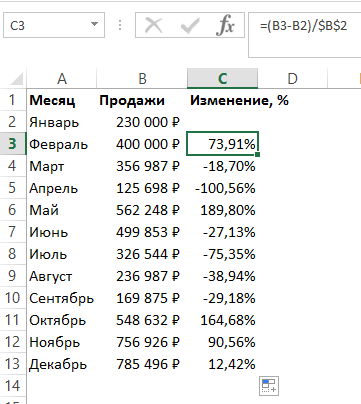
5. Прописываем формулу в ячейке D2 и спускаемся немного вниз =C2*100%/B2.
6. К ячейке, в которой высветился результат, применяем формат «Процентный». Выделяем ячейки, правой кнопкой жмем на любой из них и выбираем «Формат». Во вкладке «Число» выбираем «Процентный». Система автоматически пропишет значок %.

7. Применив нашу формулу ко всем данным, получаем результат.

Основные определения

Процент — это одна сотая часть от любого числа. Обозначающим знаком является %.

Чтобы узнать, как перевести проценты в дробь, нужно убрать знак % и разделить известное на 100, как в примере выше.

А если нужно перевести десятичную дробь в проценты — умножаем дробь на 100 и добавляем знак %. Например, 0,18 = 0,18 · 100% = 18%. Как перевести проценты в десятичную дробь — обратным действием: 18 : 100 = 0,18.

Выразить дробь в процентах просто. Для перевода сначала превратим её в десятичную дробь, а далее используем предыдущее правило.

Развивайте математическое мышление детей на наших уроках математики вместе с енотом Максом и его друзьями. Мы подобрали для вашего ребенка тысячи увлекательных заданий — от простых логических загадок до хитрых головоломок, над которыми интересно подумать. Все это поможет легче и быстрее подружиться со школьной математикой.

Второй способ нахождения процента

Второй способ нахождения процента намного проще и удобнее. Он заключается в том, что число от которого ищется процент сразу умножит на нужный процент, выраженный в виде десятичной дроби.

Например, решим предыдущую задачу этим способом. Найти 50% от 300 рублей.

Запись 50% заменяет собой запись  , а если перевести эти  в десятичную дробь, то мы получим 0,5

Теперь для нахождения 50% от 300, достаточно будет умножить число 300 на десятичную дробь 0,5

300 × 0,5 = 150

Кстати, по этому же принципу работает механизм нахождения процента на калькуляторах. Чтобы найти процент с помощью калькулятора, нужно ввести в калькулятор число от которого ищется процент, затем нажать клавишу умножения и ввести искомый процент. Затем нажать клавишу процента %

Три типа задач на проценты

Для всех видов практических задач на проценты используется универсальная формула:

p=(A/B)x100%;

где р — процент, который число А составляет от числа В. (1).

Величину р следует трактовать здесь как количество сотых долей, которые число, А составляет от числа В. Пользуясь этой формулой, можно решать три типа задач, по числу неизвестных в ней.

Задачи первого типа

Здесь необходимо найти неизвестное число процентов. Для этого используется формула (1). Вот простейший пример: сколько % от 25 составляет число 12,5?

Решение: p=(12,5/25)x100%=50%.

Задачи второго типа

Нужно найти, сколько будет р % от числа В. Из (1) можно легко получить следующую формулу:

А=(р/100)xВ. (2).

Задача. Сколько будет 13% от 6700 рублей?

Решение: А=(13/100)x6700=871 рубль.

Задачи третьего типа

Если известно, что р % от числа В равно А. Чему равно В? Из (1) следует, что

В=(100xА)/р. (3).

Задача. 7% от некоторого числа равно 777. Чему равно само число?

Решение: В=(100×777)/7=11100.

Онлайн калькулятор

Если вы уже знакомы со всеми правилами и умеете их с легкостью использовать, но ситуация срочная и нужно все быстро посчитать — можно обратиться за помощью к калькулятору. Нахождение ответа выглядит так:

• Для подсчета % от суммы: вводим известное, равное 100%, знак умножения, нужный процент, знак %.
• Чтобы вычесть %: введем известное, равное 100%, знак минус, размер процентной доли и знак %.

5 класс, урок в самом разгаре, нужно определить процент от числа как можно быстрее — поможет онлайн калькулятор. Составлять расчет быстро и точно:

• Раз
• Два
• Три
• Четыре

Но помните, что на контрольных работах и экзаменах за вас никто не решит, а калькулятор не поможет.

Приходите практиковаться! В детской школе Skysmart ученики разбирают интересные задания, проходят квесты, играют в английский на интерактивной платформе и обсуждают темы, которые им интересны. Никаких скучных упражнений — только то, что зажигает вашего ребенка. Запишите его на бесплатный вводный урок и покажите, что английский может быть увлекательным путешествием!

Примеры школьных заданий

Из запланированной дистанции в 32 км Том пробежал только 76%. Сколько километров пробежал мальчик?
Решение: для вычислений подходит первый калькулятор. В первую ячейку вставляем 76, во вторую — 32.
Получаем: Том пробежал 24.32 км.

Фермер Купер собрал с поля 500 кг кукурузы. 160 кг из этой массы оказалось неспелой. Сколько процентов от общего числа составила неспелая кукуруза?
Решение: для расчёта подходит второй калькулятор. В первое окошко записываем число 160, во второе — 500.
Получаем: 32% кукурузы оказалось неспелой.

Майкл прочитал своей подруге на ночь 112 страниц, что составляет 32% всей книги. Сколько страниц в книге?
Решение: используем для расчёта третий калькулятор. Вставляем в первую ячейку значение 112, а во вторую — 32.
Получаем: в книге 350 страниц.

Длина маршрута, по которому ходил автобус №42, составляла 48 километров. После добавления трёх дополнительных остановок расстояние от начальной до конечной станции изменилось до 78 километров. На сколько процентов изменилась длина маршрута?
Решение: используем для вычисления четвёртый калькулятор. В первую ячейку вбиваем число 78, во вторую — 48.
Получаем: длина маршрута выросла на 62.5%.

Братство металла и макулатуры в мае сдало на лом 320 кг цветного металла, а в июне на 30% больше. Сколько металла сдали ребята из братства в июне?
Решение: для расчёта будем использовать пятый калькулятор. В первую ячейку вставляем число 30, а во второе число 320.
Получаем: в июне братство сдало 416 кг металла.

Энди прорыл во вторник 3 метра туннеля, а в среду в связи с отъездом друга в Ирландию — на 22% меньше. Сколько метров туннеля прорыл Энди в среду?
Решение: в данном случае подходит шестой калькулятор. В первую ячейку вставляем 22, во вторую — 3.
Получаем: в среду мальчик прорыл 2.34 метра туннеля.

Считаем соотношения

Чтобы перевести проценты в обычное число, иногда можно использовать дроби. Например, 5% – это 1\20 числа. То есть, от 100 это будет 5.

Вот самые распространенные соотношения:

• 20% – 1\5, делим число на 5;
• 25% – 1\4, делим на 4;
• 50% – 1\2;
• 10% – 1\10;
• 5% – 1\20;
• 75% – 3\4.

В таких соотношениях сначала нужно разделить на 4, а затем умножить на 3.

Например, вы нашли в магазине вещь, которая стоит 3500. Однако, консультант говорит, что сейчас действует акция на все вещи – скидка 30%.

Вам надо посчитать новую стоимость товара.

Итак: 100%-30% = 70% – стоимость в процентах от первоначальной цены после скидки.

Новая цена составляет 2100.

Что такое проценты?

Это слово произошло от английского словосочетания Pro Centum

Прочитав это словосочетание, вы наверняка обратили внимание, что там присутствует слово цент. От этого и происходит смысл процентов

Как известно, цент — одна сотая часть от доллара. Поэтому 1% — это и есть одна сотая часть от числа.

Сейчас в процентах измеряются многие финансовые показатели:

1. налоги;
2. доли в бизнесе;
3. доходность от инвестиций;
4. премии и штрафы;
5. инфляция.

И не только финансовые:

1. рождаемость и смертность;
2. статистика удачных и неудачных браков;
3. коэффициент полезного действия.

Пример 1. Водитель таксомоторной службы отработал смену. За день его выручка составила 5 тыс. рублей. Ему необходимо отдать службе такси комиссию с этих заказов — 15%. Чтобы узнать сумму, которую должен заплатить водитель, необходимо 5 тыс. умножить на 15, после чего разделить на 100. Мы получаем результат, равный 750 рублей. Как вы уже догадались, 15% — это 15 частей из ста.

Теперь мы приведём вам обратный пример с тем же водителем такси. Так, за смену он заработал 5 тыс. рублей. Он потратил определённую часть этих денег на обязательные расходы:

1. комиссию службе такси — 750 рублей;
2. мойку автомобиля — 250 рублей;
3. топливо — 1 тыс. рублей.

Итого у водителя остаётся 3 тыс. рублей. Из заработанных 5 тыс. рублей себе он забирает только 3. Теперь наша задача посчитать, какую часть от общей выручки он может смело положить к себе в карман. Для этого нам нужно разделить 3 тыс. на 5 тыс. После чего полученный результат, равный 0,6, умножить на 100%. Получается, водитель забирает себе в карман 60% от общей выручки.

Это интересно: разрядные слагаемые — что это?

Пример 2. Четыре акционера открыли бизнес. Спустя год упорной работы он начал приносить доходы. Партнёры решили делить прибыль поровну, то есть каждому достанется по 25% от прибыли. Нам нужно посчитать, сколько денег получит каждый из них.

Допустим, бизнес приносит доход 200 тысяч рублей в месяц. Чтобы посчитать прибыль каждого из акционеров, необходимо умножить 200 тыс. на 25, и разделить на 100. Получаем результат — 50 тыс. рублей.

Пример 3. Конверсия продаж. Менеджер по продажам предлагает услуги своей компании по телефону. За месяц он совершил 800 звонков. Заинтересовались в услугах компании 280 клиентов. Для подсчёта конверсии продаж необходимо 280 разделить на 800, после чего умножить на 100. Результат будет равен 35%.

Составляем пропорцию

Пропорции нас учили составлять еще в школе. На мой взгляд, это самый удобный способ считать проценты. Как гласит математическое правило, произведение крайних членов пропорции равно произведению её средних членов.

Разберемся на примере.

Вы решили приготовить пасту и купили сыр и томатную пасту. Но, вместо кусочка сыра 150 грамм, перепутали и взяли 120. Теперь вам нужно рассчитать, сколько томатной пасты нужно положить в блюдо.

Вычислим процентную долю сыра.

150гр: 100% = 120 гр : Х, где Х масса вашего кусочка сыра.

Х = 120 × 100 / 150 = 80%

Теперь составляем пропорцию, чтобы выяснить, сколько томатной пасты нам нужно:

150 г.: 100% = Х : 80%, где Х — нужное количество масла.

Х = 80 × 150 / 100 = 120

Получается, что для пасты вам потребуется 120гр. томатов.

Пример расчета скидки

Чтобы рассчитать насколько выгодна скидка, также подойдет формула пропорций. Например, вещь стоит 2499, а скидка на нее 15%.

Узнаем цену в процентах. Для этого отнимаем 15 от 100 = 85%.

Составляем пропорцию. 2499 : 100 = Х : 85

Х = 85 × 2499 / 100

Х = 2124, 15

Не слишком выгодная цена для вещи, которую вы так долго ждали. Может быть в следующем месяце магазин даст более выгодную цену?

Как вычесть процент от суммы без помощи калькулятора

Если же требуется от уже известной суммы отнять неизвестное число, составляющее какое-то количество процентов, можно воспользоваться следующими методами:

1. Вычислить неизвестное число с помощью одного из приведенных выше способов, после чего отнять его от исходного.
2. Сразу рассчитать остающуюся сумму. Для этого от 100% отнимаем то число процентов, которое нужно вычесть, и полученный результат переводим из процентов в число любым из описанных выше способов.

Второй пример удобнее, поэтому проиллюстрируем его. Допустим, надо узнать, сколько останется, если от 4779 отнять 16%. Расчет будет таким:

1. Отнимаем от 100 (общее количество процентов) 16. Получаем 84.
2. Считаем, сколько составит 84% от 4779. Получаем 4014,36.

Как посчитать проценты, составив пропорцию

Составлять пропорции — одно из наиболее полезных умений, которому вас научили в школе. С его помощью можно посчитать любые проценты. Выглядит пропорция так:

сумма, составляющая 100% : 100% = часть суммы : доля в процентном соотношении.

Или можно записать её так: a : b = c : d.

Обычно пропорция читается как «а относится к b так же, как с относится к d». Произведение крайних членов пропорции равно произведению её средних членов. Чтобы узнать неизвестное число из этого равенства, нужно решить простейшее уравнение.

Пример 1

Для примера вычислений используем рецепт быстрого брауни. Вы хотите его приготовить и купили подходящую плитку шоколада массой 90 г, но не удержались и откусили кусочек-другой. Теперь у вас только 70 г шоколада, и вам нужно узнать, сколько масла положить вместо 200 г.

Сначала вычисляем процентную долю оставшегося шоколада.

90 г : 100% = 70 г : Х, где Х — масса оставшегося шоколада.

Х = 70 × 100 / 90 = 77,7%.

Теперь составляем пропорцию, чтобы выяснить, сколько масла нам нужно:

200 г : 100% = Х : 77,7%, где Х — нужное количество масла.

Х = 77,7 × 200 / 100 = 155,4.

Следовательно, в тесто нужно положить примерно 155 г масла.

Пример 2

Пропорция подойдёт и для расчёта выгодности скидок. Например, вы видите блузку за 1 499 рублей со скидкой 13%.

Сначала узнайте, сколько стоит блузка в процентах. Для этого отнимите 13 от 100 и получите 87%.

Составьте пропорцию: 1 499 : 100 = Х : 87.

Х = 87 × 1 499 / 100.

Заплатите 1 304,13 рубля и носите блузку с удовольствием.

Как рассчитать сумму процентов кредита по ежемесячному аннуитетному платежу

Если понятие дифференцированный кредит узнаваемо всеми, то термин «аннуитетный» не так распространён. Такой займ подразумевает погашение долга равными частями. То есть высчитать сколько средств следует вносить на счёт каждый месяц заново не придётся. На протяжении всего займового периода платежи не меняются. Однако сама ставка и процент рассчитываются немного другим способом, более сложным. Опять же, для упрощения задачи рациональнее посчитать через калькулятор процентов по кредиту.

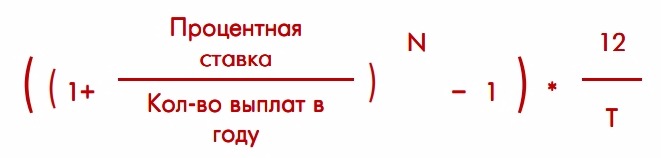
Чтобы рассчитать сумму ежемесячного платежа, не прибегая к помощи специального калькулятора процентов по кредиту, воспользуйтесь такой формулой:

Теперь расшифруем необходимые для высчитывания значения (кстати, калькулятор здесь в любом случае понадобится, иначе рискуете неправильно рассчитать сумму):

• ПСЗ – первичная сумма займа.
• ГПС – годовой процентный размер.
• КП – запланированное количество платежей по займу.

По этой формуле придётся считать платёж с возведением в степень и многоуровневым делением, поэтому проще использовать калькулятор кредита онлайн с процентами.

Аннуитетный или дифференцированный: наименьшие выплаты процентов по кредиту

Итак, рассчитывать проценты и размер ставок можно двумя методами: при помощи специального кредитного калькулятора или посчитать самостоятельно по формуле. Но один вопрос всё же остаётся нераскрытым: какая выплата окажется более выгодной – дифференцированная или аннуитетная?

По-сути, достоинства и недостатки подсчётов есть у обеих систем. Выбирать следует самостоятельно, отталкиваясь от реальных возможностей выплаты. Рекомендуется предварительно произвести расчёт процентов по кредиту с помощью калькулятора онлайн или считать самостоятельно, используя приведённые формулы. На основе полученной вычисленной информации подбирать подходящий способ выплаты займа.

Хитрости при нахождении процентов

Самый простой способ быстро все подсчитать — воспользоваться онлайн-калькулятором. У этого калькулятора очень простой интерфейс:

1. поле для введения процента;
2. поле для введения числа, процент от которого мы будем находить;
3. кнопка «Вычислить».

Вы можете легко найти такой калькулятор в интернете, вам не придётся заморачиваться с подсчётами. В принципе, это логично пользоваться всеми благами интернета. Однако в жизни бывают ситуации, когда необходимо посчитать процент от числа, но калькулятора под рукой нет.

Онлайн-калькуляторы вы можете найти на следующих сайтах:

1. calculator888.ru;
2. fin-calc.org.ua;
3. calc.by.

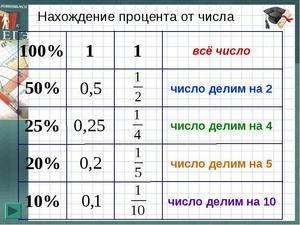
Очень простая техника нахождения процентов — деление. Но её можно использовать только с числами, на которые легко делится 100. Например, 100 легко делится на 25. Результат деления — четвёрка. Это значит, что для нахождения 25% от суммы необходимо просто разделить её на 4. По такой же схеме можно найти 10, 20 и 50% от нужной вам суммы.

Конечно же, необязательно считать в уме всё, вы можете разделить все на калькуляторе. Главное, что вы понимаете, как работает эта схема, и сможете легко применить её на практике.

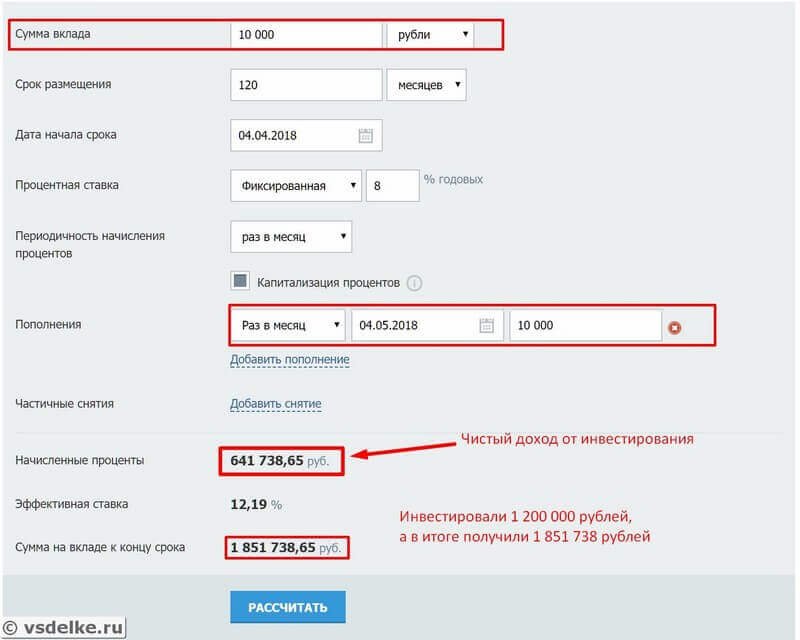
Знание того, как посчитать проценты от процентов поможет вам планировать ваши доходы. Например, при депозитном вкладе с процентной ставкой 10% в год ваш доход за 2 года составит 21%. Потому что во втором году проценты начислялись уже на сумму, накопленную в течение первого года. А это 110% от суммы первоначального взноса.

Как отнять от суммы процент с помощью онлайн-калькулятора

Наконец, сейчас в сети достаточно сайтов, где реализована функция онлайн-калькулятора. В этом случае даже не требуется знания того, как посчитать процент от суммы: все операции пользователя сводятся к вводу в окошки нужных цифр (или передвижению ползунков для их получения), после чего результат сразу высвечивается на экране.

Особенно эта функция удобна тем, кто рассчитывает не просто абстрактный процент, а конкретный размер налогового вычета или сумму госпошлины. Дело в том, что в этом случае вычисления сложнее: требуется не только найти проценты, но и прибавить к ним постоянную часть суммы. Онлайн-калькулятор позволяет избежать подобных добавочных вычислений. Главное — выбрать сайт, пользующийся данными, которые соответствуют действующему закону.

***

Больше полезной информации — в рубрике «Другое». 

Как считать проценты на калькуляторе: простейшие способы

Учитывая, что сегодня так называемые «счетные машинки» находятся на столе у любого школьника, продавца или бухгалтера, а также на любом телефоне и компьютере, нам не остается ничего другого, как считать проценты на калькуляторе. Мы не зря в начале статьи вспомнили школу и ваш дружный (а может и не дружный) шестой класс. Отбросив эти романтические переживания, перейдем к подсчету процентов.

Как вычислить процент от суммы: 1 способ

Давайте найдем необходимый процент с помощью простого примера. Допустим, вам необходимо найти 25% от суммы в 1000 рублей. Решаем следующий пример:

1000*25:100= 250

Как вычислить процент от суммы: 2 способ

Этот подсчет еще проще:

1000*0,25=250

Как вычислить процент от суммы: 3 способ

Ну и вычисление для совсем ленивых:

1000*25%=250

Вот вы и узнали простые способы, как посчитать проценты на калькуляторе. Мы уверены, что вы о них знали со школьной скамьи, и просто напомнили вам. Теперь вы можете применить эти знания и без проблем вычислить проценты по кредиту или по вкладу, самостоятельно подсчитав сумму процентов.

Как считать проценты в excel?

Если у вас под рукой имеется компьютер или ноутбук с операционной системой Windows, вам не составит большого труда подсчитать процент от необходимой суммы. Приведем для этого простой пример.

Нам необходимо найти 8% от 358.

1. Открываем Excel.
2. Находим свободную строку.
3. Вводим данные.
4. Ставим знак «=» и делаем подсчет.
5. Получаем 28,64.

Аналогично к подсчетам на калькуляторе, вы можете ввести в Excel знак %, и это тоже будет правильно.

Иногда нам необходимо узнать процентный показатель от суммы.

1. К примеру, у нас есть список сотрудников и сумма, на которую они произвели продаж. Помимо этого, известна сумма возвратов. По этим данным мы рассчитываем процент возвратов по товарам.
2. Просчитаем процент для первого показателя в списке — процент возвратов некоего Петрова.
3. Для начала составляем пропорцию, где 100% — это 35682(сумма продаж Петрова). х% — 2023 (сумма возвратов Петрова).
4. Решаем эту пропорцию по формуле, известной нам со школы.
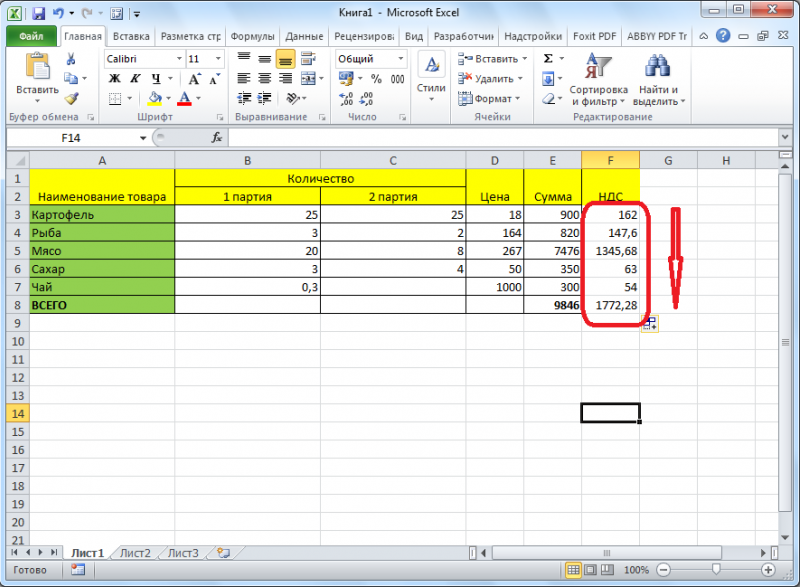
5. Прописываем формулу в ячейке D2 и спускаемся немного вниз =C2*100%/B2.
6. К ячейке, в которой высветился результат, применяем формат «Процентный». Выделяем ячейки, правой кнопкой жмем на любой из них и выбираем «Формат». Во вкладке «Число» выбираем «Процентный». Система автоматически пропишет значок %.

7. Применив нашу формулу ко всем данным, получаем результат.

Видео: как посчитать проценты от суммы?

Расчет при помощи онлайн-калькулятора

Вычислить процент при помощи обычного онлайн-калькулятора не представляет труда.

Многие из них сделаны по принципу стандартных устройств, а потому вычисления проходят по выше указанной схеме.

Если же на онлайн-калькуляторе нет кнопки «%», вычисления могут проходить двумя способами:

1. Необходимо разделить процент на 100 и умножить на данное число. Пример: выделить 15% от 300. 15/100 = 0,15; 0,15*300 = 45.
2. Разделить число на 100 и умножить на процент: 300/100 = 3; 3*15 = 45.

Если нахождение необходимо для оплаты кредита, ипотеки, ОСАГО или налоговых вычетов, можно воспользоваться специализированными калькуляторами. Их легко найти по поиску.

Они значительно отличаются от простых калькуляторов: например, при расчете стоимости ОСАГО потребуется выбрать тип автомобиля, мощность двигателя, указать стаж, возраст и область и некоторые другие данные. Исходя из этих данных, калькулятор сосчитает примерную среднюю стоимость в рублях полиса.

Стоит отметить: к сожалению, полученная при таких подсчетах сумма лишь примерна – правильные данные будут рассчитаны специалистом при личном обращении.

Как найти базовую сумму исходя из ее процента

В некоторых случаях нам может быть известно какое-либо число и процент, которое оно составляет от базового числа. Нам необходимо определить значение. Например, нам может быть дана сумма 67, которое составляет 23% от базового числа. Каково же само базовое число?

Для решения этой задачи нам необходимо 67 разделить на 23 и умножить на 100. Формула вычисления процента выглядит следующим образом:

67 / B * 100 = A

Подставляем значения:

67 / 23 * 100 = 293, 31 (десятые после запятой можем округлить)

Проверяем полученный результат с помощью формулы из первого способа:

293, 31 / 100 * 23 = 67

Всё сошлось.

Расчет при помощи известных соотношений

Если указанный выше способ слишком сложен, можно воспользоваться более простым вариантом. Он основан на том, что 1% = 0,01.

То есть для нахождения процента, достаточно умножить число на цифру переведенной в десятичную дроби.

В виде формулы это выглядит следующим образом:

Y = (n%/100)*X.

Пример.

Сколько будет 15% от 300.

1. 15%/100 = 0,15.
2. 0,15*300 = 45.

Помимо десятичных дробей можно пользоваться переведенный простыми дробями – для этого достаточно записать в числители дроби процент, а в знаменателе – 100. Для простоты ниже даны некоторые самые популярные дроби:

1. 1/8 = 12,5% — данные делятся на 8;
2. 1/5 = 20% — делим на 5;
3. 1/4 = 25% — делится на 4;
4. 1/2 = 50% — делится на 2.

Возьмите на заметку: некоторые простые дроби не смогут полностью заменить десятичные: например, 1/3 – 33,(3)%, то есть бесконечное неделимое значение, заменить его полностью на 33% не получится.

Составление пропорций

Задачи на проценты могут решаться с помощью пропорций. Составление соотношений с процентами производится в следующей последовательности:

1. Базовое число A принимается за 100%. Число А в цифровом обозначении будет первым членом пропорции, оно соответствует 100%.
2. Другие члены пропорции — это часть исходного числа (обозначение B) и соответствующие этой части (p).

Пропорция будет иметь такой вид:

\(A\;/\;B\;=\;100\%\;/\;p\%\)

Пример:

500 — 100%

250 — 50%

Пропорция будет выглядеть так: 500 / 250 = 100% / 50%.

В задачах на проценты неизвестный член пропорции обозначают буквой х. Для его определения применяют основное свойство пропорций: при умножении крайних членов между собой получится число, равное произведению средних членов. Следовательно, чтобы найти х, необходимо крест-накрест перемножить члены соотношения. При этом можно вывести следующие формулы:

• A = 100 % × B / p %;
• B = A × p % / 100 %;
• p % = 100 % × B / A.

Пример

Зарплата преподавателя равна 25 000 рублей, премия составляет 10% от заработной платы. Определите размер премиальной выплаты.

Составим пропорцию: 

25 000 — 100%

х — 10%.

По основному свойству пропорций:

25 000 × 10 = 100 × x

x = (25 000 × 10) / 100 = 2 500

Ответ: премия равна 2 500 рублей.