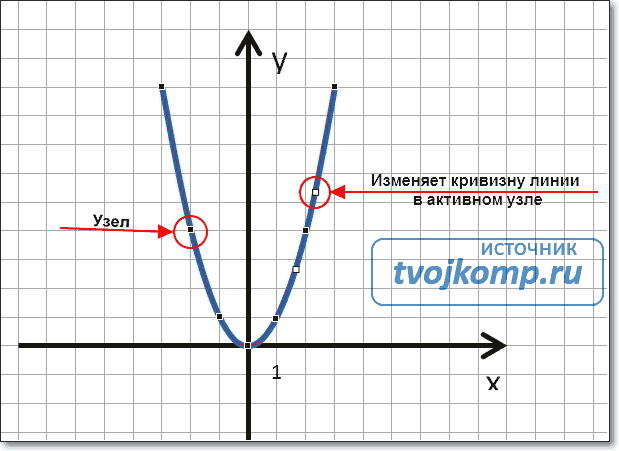
Свойства функций синуса, косинуса, тангенса и котангенса и их графики

Пошаговая инструкция построения графика функции в Excel 2007

1. Запускаем программу, которая создаст новый чистый лист книги Excel. Подписываем два столбца (B и С), в одном из которых будет записан аргумент x, а в другом — функция y.
2. Заносим в столбец B, значения аргументов x, начиная с ячейки B3. Можно воспользоваться автоматическим копированием ячеек, предварительно задав шаг (разница между ближайшими значениями аргумента). Значения аргумента x можно задать произвольно, но чаще вводят значения близкие к нулю с учетом отрицательных и положительных значений. Очень хорошо будет смотреться график, если значения будут браться симметрично относительно нуля. Предлагаем выбрать значения в промежутке от -3 до +3 с шагом 0,1. В итоге вы получите 60 значений, по которым график функции будет проложен весьма плавно.
3. Далее, в ячейку C3 забьём формулу функции синуса или ту, которую вам надо построить. Если помните тригонометрию, то функция синуса записывается в виде y = sin x.
4. Однако формулы в Excel отличаются от записей математических формул, и всегда начинаются со знака равно — «=». В нашем примере, вы должны записать в ячейке C3 формулу вида = SIN(B3).
5. Забивать формулу в каждой новой строке очень долго и неудобно (представляете, нужно вбить 60 раз!). Для того чтобы формула была в каждой ячейке необходимо «протянуть» формулу из первой ячейки на все остальные. При этом ссылка на ячейку, откуда берётся значение аргумента будет смещаться построчно.
6. Для этого щёлкаем на ячейке с набранной формулой. В правом нижнем углу ячейки должен появиться небольшой квадратик. Следует навести на него курсор мышки, и когда квадратик превратится в крестик, нажимаем правую кнопку и копируем «протягиванием» формулу вниз на нужное количество ячеек.
7. Переходим к построению графика функции. Заходим в Меню «Вставка» -> «Диаграмма» и выбираем подходящую точечную диаграмму. Жмем волшебную кнопку .
8. В открывшемся окне щелкаем вкладку «Ряд». Добавляем ряд нажатием кнопки .
9. В этом окне нужно задать, из какого диапазона будут выбраны числа для графика. Чтобы выбрать нужные ячейки, следует щёлкнуть поочередно по кнопкам.
10. После этого выделим те ячейки, откуда будут выбраны значения для x и y.
11. Последним шагом станет нажатие кнопки .

Графики функций с модулем

Для качественного усвоения материала необходимо понимать, что такое модуль. Краткую информацию о нём можно найти на странице Математические формулы и таблицы в справочном материале Горячие формулы школьного курса математики.

Применение модуля тоже представляет собой геометрическое преобразование графика. Не буду создавать сверхподробный мануал, отмечу только те моменты, которые, с моей точки зрения, реально пригодятся для решения других задач по вышке.

Сначала посмотрим, что происходит, когда модуль применяется к АРГУМЕНТУ функции.

Правило: график функции  получается из графика функции  следующим образом: при  график функции  сохраняется, а при  «сохранённая часть» отображается симметрично относительно оси .

Пример 22

Построить график функции

И снова вечная картина: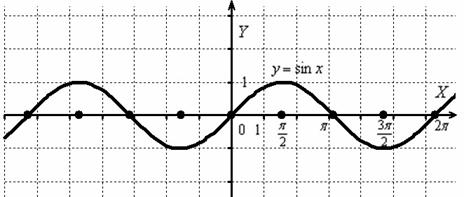
Согласно правилу, при  график сохраняется: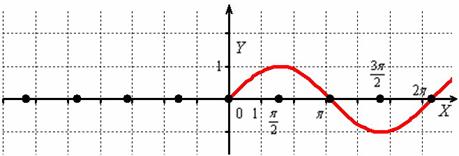
И сохранившаяся часть отображается симметрично относительно оси   в левую полуплоскость: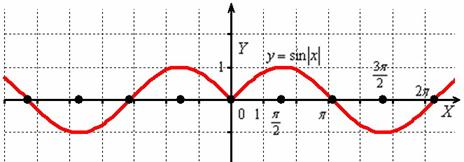

Действительно, функция  – чётная, и её график симметричен относительно оси ординат. Поясню детальнее смысл симметрии. Посмотрим на два противоположных значения аргумента, например, на  и . А какая разница? Модуль всё равно уничтожит знак «минус»: , то есть значения функции будут располагаться на одной высоте.

Функцию от модуля можно расписать в так называемом кусочном виде по следующему правилу: . В данном случае: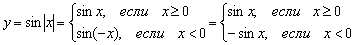

То есть, правая волна графика  задаётся функцией , а левая волна – функцией  (см. Пример 13).

Пример 23

Построить график функции

Аналогично, ветвь «обычной» экспоненты  правой полуплоскости отображаем симметрично относительно оси  в левую полуплоскость:
Распишем функцию в кусочном виде: , то есть правая ветвь задаётся графиком функции , а левая ветвь графиком .

Модуль не имеет смысл «навешивать» на аргумент чётной функции:  и т.п. (проанализируйте, почему).

И, наконец, завершим статью весёлой нотой – применим модуль к САМОЙ ФУНКЦИИ.

Правило: график функции  получается из графика функции  следующим образом: часть графика , лежащая НАД осью  сохраняется, а часть графика , лежащая ПОД осью  отображается симметрично относительно данной оси.

Странно, что широко известный график модуля «икс» оказался на 24-й позиции, но факт остаётся фактом =)

Пример 24

Построить график функции

Сначала начертим прямую, известную широкому кругу лиц: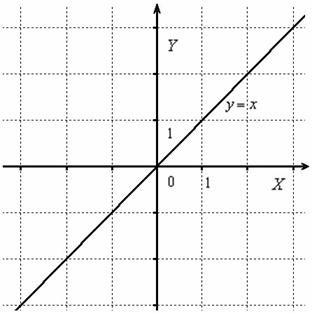
Часть графика, которая ВЫШЕ оси , остаётся неизменной, а часть графика, которая НИЖЕ оси  – отображается симметрично в верхнюю полуплоскость: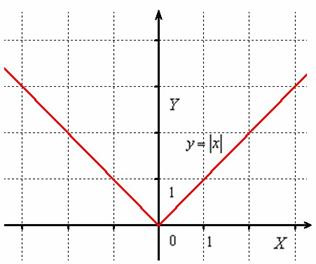

Модуль функции также раскрывается аналитически в кусочном виде:

Внимание! Формула отличается от формулы предыдущего пункта!

В данном случае: , действительно, правый луч задаётся уравнением , а левый луч – уравнением .

Кстати,  – редкий экземпляр, когда можно считать, что модуль применён, как к аргументу: , так и  к самой функции: . Изучим более «жизненную» ситуацию:

Пример 25

Построить график функции

Сначала изобразим график линейной функции :
То, что ВЫШЕ оси абсцисс – не трогаем, а то, что НИЖЕ – отобразим симметрично относительно оси  в верхнюю полуплоскость:

Согласно формуле , распишем функцию аналитически в кусочном виде: .

Или, упрощая оба этажа: , то есть правый луч задаётся функцией , а левый луч – функцией . Сомневающиеся могут взять несколько значений «икс», выполнить подстановку и свериться с графиком.

На какие функции модуль «не действует»? Модуль бессмысленно применять к неотрицательным функциям. Например: . Экспоненциальная функция и так полностью лежит в верхней полуплоскости: .

Всё возвращается на круги своя, синусом начали, синусом и закончим. Как в старой доброй сказке:

Пример 26

Построить график функции .

Изобразим сами знаете что =)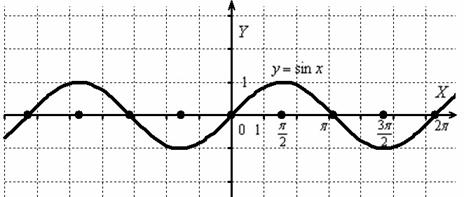

И снова – то, что находиться в верхней полуплоскости – оставим в покое, а содержимое подвала – отобразим симметрично относительно оси :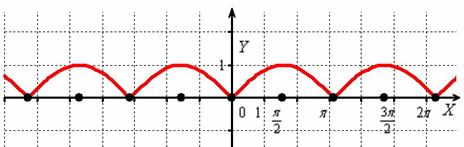

Кстати, понятен ли вам неформальный смысл такого симметричного отображения? Модуль «съедает» у  отрицательных чисел знак и делает их положительными, именно поэтому «подвальные» точки занимают противоположные места в верхней полуплоскости.

Распишем функцию в кусочном виде:

Решив два простейших школьных неравенства , получаем: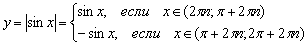, где  – любое целое число.

Да, статья была не самой приятной, но крайне необходимой. Однако повествование завершилось и стало немножко грустно =) Чем-то напомнило мне всё это урок про метод Симпсона, который тоже создавался в марте, и тоже достаточно долгое время. Наверное, громоздкие вещи пишутся по сезону =)

Желаю успехов!

(Переход на главную страницу)

Угол поворота

Определения, данные выше, относятся к острым углам. В тригонометрии вводится понятие угла поворота, величина которого, в отличие от острого угла, не ограничена рамками от 0 до 90 градусов.Угол поворота в градусах или радианах выражается любым действительным числом от -∞ до +∞. 

В данном контексте можно дать определение синуса, косинуса, тангенса и котангенса угла произвольной величины. Представим единичную окружность с центром в начале декартовой системы координат.

Начальная точка A с координатами (1, ) поворачивается вокруг центра единичной окружности на некоторый угол α и переходит в точку A1. Определение дается через координаты точки A1(x , y). 

Синус (sin) угла поворота

Синус угла поворота α — это ордината точки A1(x , y). sin α=y

Косинус (cos) угла поворота

Косинус угла поворота α — это абсцисса точки A1(x , y). cos α=х

Тангенс (tg) угла поворота

Тангенс угла поворота α — это отношение ординаты точки A1(x , y) к ее абсциссе. tg α=yx

Котангенс (ctg) угла поворота

Котангенс угла поворота α — это отношение абсциссы точки A1(x , y) к ее ординате. ctg α=xy

Синус и косинус определены для любого угла поворота. Это логично, ведь абсциссу и ординату точки после поворота можно определить при любом угле. Иначе обстоит дело с тангенсом и котангенсом. Тангенс не определен, когда точка после поворота переходит в точку с нулевой абсциссой (, 1) и (, -1). В таких случаях выражение для тангенса tg α=yx просто не имеет смысла, так как в нем присутствует деление на ноль. Аналогично ситуация с котангенсом.  Отличием состоит в том, что котангенс не определен в тех случаях, когда в ноль обращается ордината точки.

Важно помнить!

Синус и косинус определены для любых углов α.

Тангенс определен для всех углов, кроме α=90°+180°·k, k∈Z (α=π2+π·k, k∈Z)

Котангенс определен для всех углов, кроме α=180°·k, k∈Z (α=π·k, k∈Z)

При решении практических примеров не говорят «синус угла поворота α». Слова «угол поворота» просто опускают, подразумевая, что из контекста и так понятно, о чем идет речь. 

Нужна помощь преподавателя?
Опиши задание — и наши эксперты тебе помогут!

Описать задание

Тригонометрический круг

Графически соотношение упомянутых величин можно представить следующим образом:

Окружность, в данном случае, представляет собой все возможные значения угла α – от 0° до 360°. Как видно из рисунка, каждая функция принимает отрицательное или положительное значение в зависимости от величины угла. Например, sin α будет со знаком «+», если α принадлежит I и II четверти окружности, то есть, находится в промежутке от 0° до 180°. При α от 180° до 360° (III и IV четверти) sin α может быть только отрицательным значением.

Значения α равные 30°, 45°, 60°, 90°, 180° и так далее – называют частными случаями. Значения тригонометрических функций для них просчитаны и представлены в виде специальных таблиц.

Данные углы выбраны отнюдь не случайно. Обозначение π  в таблицах стоит для радиан. Рад  – это угол, при котором длина дуги окружности соответствует ее радиусу. Данная величина была введена для того, чтобы установить универсальную зависимость, при расчетах в радианах не имеет значение действительная длина радиуса в см.

Углы в таблицах для тригонометрических функций соответствуют значениям радиан:

Итак, не трудно догадаться, что 2π – это полная окружность или 360°.

Особенности использования тригонометрических функций в Excel

Синтаксис функции SIN:

=SIN(число)

Синтаксис функции SINH:

=SINH(число)

Синтаксис функции COS:

=COS(число)

Синтаксис функции COSH:

>=COSH(число)

Каждая из приведенных выше функций принимает единственный аргумент число, который характеризует угол, заданный в радианах (для SIN и COS) или любое значение из диапазона вещественных чисел, для которого требуется определить гиперболические синус или косинус (для SINH и COSH соответственно).

Примечания 1:

1. Если в качестве аргумента любой из рассматриваемых функций были переданы текстовые данные, которые не могут быть преобразованы в числовое значение, результатом выполнения функций будет код ошибки #ЗНАЧ!. Например, функция =SIN(“1”) вернет результат 0,8415, поскольку Excel выполняет преобразование данных там, где это возможно.
2. В качестве аргументов рассматриваемых функций могут быть переданы логические значения ИСТИНА и ЛОЖЬ, которые будут интерпретированы как числовые значения 1 и 0 соответственно.
3. Все рассматриваемые функции могут быть использованы в качестве формул массива.

Примечения 2:

1. Синус гиперболический рассчитывается по формуле: sinh(x)=0,5*(ex-e-x).
2. Формула расчета косинуса гиперболического имеет вид: cosh(x)=0,5*( ex+e-x).
3. При расчетах синусов и косинусов углов с использованием формул SIN и COS необходимо использовать радианные меры углов. Если угол указан в градусах, для перевода в радианную меру угла можно использовать два способа:

• Функция РАДИАНЫ (например, =SIN(РАДИАНЫ(30)) вернет результат 0,5;
• Выражение ПИ()*угол_в_градусах/180.

В Microsoft Excel 2007 достаточно просто строить диаграммы и графики различных видов. Поэтому построить график какой-нибудь стандартной математической функции в Excel не составит особого труда. В этом обучающем материале по информатике будет рассмотрен процесс построения графика функции синуса в Microsoft Excel 2007.

Описывать процесс создания мы будем на примере Microsoft Excel 2007 (уже устаревшая, но очень хорошая версия программы). Процесс построения графика в более свежем Microsoft Excel 2010 будет отличаться лишь в некоторых деталях.

Электронные таблицы Excel изначально были созданы компанией Microsoft для вычислений. Результаты наших вычислений мы будем применять в качестве исходных данных для построения графика.

Построение синусоиды в excel

Как построить график синусоиды в Excel.

Допустим имеется функция синусоиды, заданной уравнением y=sin4*x. Формула в Excel имеет вид:

=SIN(4*C4)

Требуется построить график функции.

Функция в данном случае непрерывная, поэтому по оси x ограничим интервалом от 1 до -1, шаг возьмём 0,1.

В итоги у нас должна получится таблица вида:

Переходим на вкладку Вставка -> Точечная с гладкими кривыми и маркерами.

Появится область графика, кликаем на белую область правым указателем мыши, выскакивает меню, далее Выбрать данные, появляется окно Выбора источника данных, выбираем весь диапазон данных нашей синусоиды в ячейках, затем Ок.

В итоги у нас получается график вида.

Также вид графика тоже можно настроить через конструктор и дополнительные инструменты.

трюки • приёмы • решения

Использование диаграмм Excel — хороший способ отображения графиков математических и тригонометрических функций. В этой статье описываются два метода построения графика функции: с одной переменной с помощью точечной диаграммы и с двумя переменными с помощью 3D-диаграммы.

Построение графиков математических функций с одной переменной

Точечная диаграмма (известная как диаграмма XY в предыдущих версиях Excel) отображает точку (маркер) для каждой пары значений. Например, на рис. 140.1 показан график функции SIN. На диаграмму наносятся рассчитанные значения у для значений х (в радианах) от -5 до 5 с инкрементом (приращением) 0,5. Каждая пара значений х и у выступает в качестве точки данных в диаграмме, и эти точки связаны линиями.

Рис. 140.1. Диаграмма представляет собой график функции SIN(x)

Функция выражается в таком виде: у = SIN(x) .

Соответствующая формула в ячейке В2 (которая копируется в ячейки, расположенные ниже) будет следующей: =SIN(A2) .

Чтобы создать эту диаграмму, выполните следующие действия.

1. Выделите диапазон А1:В22 .
2. Выберите Вставка ► Диаграммы ► Точечная ► Точечная с прямыми отрезками и маркерами.
3. Выберите макет диаграммы, который вам нравится, а затем настройте его.

Измените значения в столбце А для построения графика функции при различных значениях х. И, конечно, вы можете использовать любую формулу с одной переменной в столбце В. Вот несколько примеров, которые приводят к построению интересных графиков: =SIN(ПИ()*A2)*(ПИ()*A2) =SIN(A2)/A2 =SIN(A2^3)*COS(A2^2) =НОРМ.РАСП(A2;0;1;ЛОЖЬ)

Чтобы получить более точную диаграмму, увеличьте количество значений для построения графика и сделайте приращение в столбце А меньше.

Вы можете использовать онлайн наш файл примера графиков математических функций с одной переменной, расположенной в Excel Web Apps при помощи Skydrive, и внести свои данные (изменения не будут сохраняться) или скачать себе на компьютер, для чего необходимо кликнуть по иконке Excel в правом нижнем углу. Это бесплатно

Построение графиков математических функций с двумя переменными

Вы также можете строить графики функций, которые используют две переменные. Например, следующая функция рассчитывает z для различных значений двух переменных (х и у): =SIN($A2)*COS($B1)

На рис. 140.2 приведена поверхностная диаграмма, которая рассчитывает значение z для 21 значения х в диапазоне от -3 до 0 и для 21 значения у в диапазоне от 2 до 5. Для х и у используется приращение 0,15.

Рис. 140.2. Использование трехмерной поверхностной диаграммы для построения графика функции с двумя переменными

Значения х находятся в диапазоне А2:А22 , а значения у — в диапазоне B1:V1 .

Формула в ячейке В2 копируется в другие ячейки таблицы и имеет следующий вид: =SIN($A2)*C0S(B$1) .

Чтобы создать диаграмму, выполните приведенные ниже действия.

1. Выделите диапазон A1:V22 .
2. Выберите Вставка ► Диаграммы ► Другие ► Поверхность.
3. Выберите макет диаграммы, который вам нравится, а затем настройте его.

Пока значения х и у имеют равные приращения, вы можете задавать любую формулу с двумя переменными. Вам, возможно, потребуется настроить начальные значения и значение приращения для х и у. Для увеличения сглаживания используйте больше значений х и у при меньшем приращении. Вот другие формулы, которые вы можете попробовать: =SIN(КОРЕНЬ($A2^2+B$1^2)) =SIN($A2)*COS($A2*B$1) =COS($A2*B$1)

Функция SIN в Excel используется для вычисления синуса угла, заданного в радианах, и возвращает соответствующее значение.

Функция SINH в Excel возвращает значение гиперболического синуса заданного вещественного числа.

Функция COS в Excel вычисляет косинус угла, заданного в радианах, и возвращает соответствующее значение.

Функция COSH возвращает значение гиперболического косинуса заданного вещественного числа.

7 Графики синуса и косинуса

Построим график функции . При этом нам опять пригодятся
часы из разд. 2.1.

Если , то, очевидно, . Когда возрастает от 0 до
, число возрастает от 0 до 1 (представьте себе,
как меняется ордината конца стрелки на наших фирменных часах).
Участок графика для от 0 до изображен на
рис. .
При

Чем ближе к , тем более полого идет наша кривая. Это
происходит потому, что проекция конца стрелки на ось
ординат, колеблясь по отрезку , быстрее всего
движется в середине отрезка и замедляется у его краев: мы
это уже обсуждали в разд. 2.1.

симметричны относительно прямой

Задача 7.1  
Запишите уравнение прямой, касающейся графика функции
в точке с координатами .

Кривая на рис б
центрально симметрична относительно точки
с координатами ; это следует из другой формулы
приведения:
(рис. б).

После того, как у нас есть участок графика функции для

, весь график строится уже просто. В самом деле,
когда конец стрелки прошел путь , стрелка вернулась
в исходное положение; при дальнейшем движении все будет
повторяться. Значит, график будет состоять из таких же кусков,
как на рис б. Окончательно график функции
выглядит так, как на рис. .

Теперь построим график функции . Можно было бы строить его так же, как
мы строили график синуса. Мы, однако, изберем другой путь,
который позволит использовать уже имеющуюся у нас информацию.

Именно, воспользуемся формулой приведения
. Эту формулу можно понимать так: функция
принимает те же значения, что и функция , но на
раньше. Например, функция принимает значение 1 при
, а функция
принимает это же
значение уже при . На графике это означает следующее: для
каждой точки графика есть точка графика ,
у которой ордината та же, а абсцисса на меньше
(рис. ).

сдвинуть график

Итак, мы выяснили, что график косинуса получается преобразованием
(сдвигом) из графика синуса. Случаи, когда график одной функции
можно получить преобразованием из графика другой функции,
интересны и сами по себе, поэтому скажем о них несколько слов.

Как, например, будет выглядеть график функции ? Ясно,
что ординаты точек этого графика получаются из ординат
соответствующих точек графика умножением на 2, так что
наш график изобразится сплошной кривой на рис. . Можно
сказать, что график получается из графика растяжением в два раза вдоль оси
ординат.

сжатием в 2 раза к оси ординат.

Попробуем еще построить график функции 
.
Понятно, что он должен получаться каким-то преобразованием из
графика . На первый взгляд может показаться, что это
преобразование — сдвиг влево на вдоль оси абсцисс, по
аналогии с тем, что изображено на рис. . Однако, если
бы это было так, то вышло бы, например, что функция

принимает значение 1 при

, что не соответствует действительности
(проверьте!). Правильно рассуждать так:
, так что функция
принимает те
же значения, что и функция , но на раньше. Так
что сдвиг влево — не на
, а на (рис. ).

Кривые, являющиеся графиками функций
, где ,
, называются синусоидами. Заметим, что кривой
«косинусоида» вводить не надо: как мы видели, график косинуса
— это та же кривая, что и график
синуса, только иначе
расположенная относительно осей координат.

Задача 7.2  
Каковы координаты точек, помеченных на
рис.  вопросительными знаками?

Задача 7.3  
Возьмите свечу, тонкий лист бумаги и острый нож. Намотайте лист
бумаги на свечу в несколько слоев и аккуратно разрежьте эту свечу
вместе с бумагой наискосок ножом. Теперь разверните бумагу. Вы
увидите, что она оказалась разрезанной по волнистой линии.
Докажите, что эта волнистая линия является синусоидой.

Задача 7.4  
Постройте графики функций:

Замечание. Если вы строите графики
тригонометрических функций на клетчатой бумаге, удобно выбрать
немного разные масштабы по осям, с тем чтобы на оси абсцисс
числу  соответствовало целое число клеточек. Например, часто
выбирают такой масштаб: по оси ординат отрезок длины 1 занимает
две клеточки, по оси абсцисс отрезок длины занимает 6
клеточек.

Задача 7.5  
Постройте графики функций:
а)
;
б)
.

Посмотрим, как выглядят на графиках уже известные нам решения
уравнений и . Эти решения являются
абсциссами точек пересечения горизонтальной прямой
с графиком функций (соответственно ). На
рис. , хорошо видны две серии решений,
получающихся при .

По графикам синуса и косинуса видно, на каких промежутках эти
функции возрастают, а на каких убывают. Ясно, например, что
функция возрастает на отрезках
,

,
,…- одним словом, на
всех отрезках
, где
,
и убывает на всех отрезках
, где

.

Задача 7.6  
На каких отрезках возрастает и на каких убывает
функция ?

Задача 7.7  
Сравните числа:

Задача 7.8  
Расположите в порядке возрастания:
, , , , , .

        Написать комментарий

Определение 3: Дифференциальное уравнение

Мы описали поведение синуса определенными уравнениями. Вкратце это будет выглядеть так:

Эта красота означает следующее:

Наша текущая позиция — y

Наше ускорение (2-я производная, или у”) — обратно нашей текущей позиции (-y)

Это справедливо и для синуса, и для косинуса. Сначала я просто ненавидел это определение; оно такое непохожее на нашу визуализацию. Я не понимал, что оно описывало суть синуса: «ускорение, обратное текущей позиции».

И вспомните как синус и е связаны? Ну, e^x можно описать уравнением:

То же уравнение с положительным знаком («ускорение равно текущей позиции»)! Когда синус — это «высота окружности», очень тяжело проследить связь с е.

Одним из моих серьезнейших математических сожалений является то, что я еще не изучил дифференциальные уравнения. Но я хочу это сделать, и подозреваю, что правильное понимание синуса и экспоненты сыграют в этом решающую роль.

Примеры использования функций SIN, SINH, COS и COSH в Excel

Пример 1. Путешественник движется вверх на гору с уклоном в 17°. Скорость движения постоянная и составляет 4 км/ч. Определить, на какой высоте относительно начальной точке отсчета он окажется спустя 3 часа.

Таблица данных:

Для решения используем формулу:

=B2*B3*SIN(РАДИАНЫ(B1))

Описание аргументов:

• B2*B3 – произведение скорости на время пути, результатом которого является пройденное расстояние (гипотенуза прямоугольного треугольника);
• SIN(РАДИАНЫ(B1)) – синус угла уклона, выраженного в радианах с помощью функции РАДИАНЫ.

В результате расчетов мы получили величину малого катета прямоугольного треугольника, который характеризует высоту подъема путешественника.

Определение 2: Бесконечный ряд

Я спрятал слона в комнате: как мы вообще вычисляем синус? Мой калькулятор, что, каждый раз рисует окружность и замеряет его?

Рад вам поведать, как можно вычислить синус без окружностей.

Синус — это ускорение в сторону, противоположную тому, где вы находитесь.

Пользуясь нашим примером с банковским счётом: представьте, что ваш шеф каждую неделю решил менять вашу зарплату на сумму, противоположную текущей на вашем банковском счёте. Если у вас сейчас есть 50 рублей, на следующей неделе шеф выдаст на 50 рублей меньше. Конечно, поскольку ваш доход будет 75 рублей, вы всё еще будете в плюсе (75 — 50) но в итоге ваш баланс уменьшится, поскольку «прибавки» шефа превзойдут ваши доходы.

Но не отчаивайтесь! Как только баланс становится отрицательным (скажем, у вас -50 рублей), ваш босс выдаст вам на целых 50 рублей больше. Затем снова баланс станет отрицательным (с его ростом шеф выдает всё меньше денег), и так будет продолжаться постоянно. Баланс будет то положительный, то нулевой, то отрицательный.

Этот пример также поясняет, почему в нейтральной точке (в 0) скорость синуса максимальна: когда вы на максимуме, вы начинаете падать и собирать всё больше «отрицательных прибавок», которые довольно быстро тянут вас к 0. После прохождения 0 вы начинаете получать наиболее значительные положительные прибавки и замедляетесь., потому что как только уходите в плюс, шеф опять начинает отнимать от вашей зарплаты.

Между прочим: поскольку синус — это ускорение, обратное к вашему текущему положению, а окружность сделана из горизонтальной и вертикальной синусоиды… вы поняли! Круговое движение может быть описано как «постоянное движение в направлении, противоположном текущей позиции, по направлению к горизонтальному и вертикальному центру».

π без картинок

Представьте себе слепого пришельца, который может различать только тени света и темноты. Можете ли вы объяснить ему, что такое π? Довольно сложно пояснить в такой ситуации понятие длины окружности, верно?

Давайте вернемся немного назад. Синус — это циклическая функция. Это означает, что значит ее значения должны…повторяться! Синус начинается с 0, идет к 1, к 0, к -1, к 0 и так далее.

Давайте определим π как время, за которое синус поднимается с 0 до 1, и обратно возвращается к 0. Вау! Теперь и мы используем π без всяких окружностей!

• Синус — это плавное передвижение вперёд-назад
• π — это время движения синуса с 0 до 1 и обратно до 0
• n * π (0 * π, 1 * π, 2 * π и т.д.) — это момент времени, в котором синус равен 0
• 2 * π, 4 * π, 6 * π и т.д. — полные периоды синуса.

Ага! Вот почему π встречается в таком количестве формул! π не «принадлежит» окружностям больше, чем 0 или 1 — π касается возвращения синуса в центр! Окружность — это пример фигуры, которая повторяется и возвращается в центр каждые 2*π единиц. Но вибрации, скачки и т.д. возвращаются к центру каждый π!

Вопрос: если π — это половина естественного периода, почему оно длится вечно (является иррациональным числом)?

Можно я отвечу вопросом на вопрос, А почему длина диагонали «единичной окружности» равна квадратному корню из 2, который также уходит в бесконечность?

Но да, я понимаю, что это философски не удобно, когда природа ведет себя произвольно. Но что поделаешь…

§ 59. Графическое изображение синусоидальных переменных величин

Практика остановила свой выбор на синусоидальных изменениях переменных электрических величин. В дальнейшем, говоря о переменном токе, э.д.с., напряжении и магнитном потоке, мы будем считать их изменяющимися по закону синуса.

Пусть мы имеем радиус-вектор ОА (рис. 124) произвольной длины. Будем вращать с постоянной скоростью вектор вокруг точки О против часовой стрелки. Конец вектора будет описывать окружность, а угол α, на который поворачивается вектор, будет меняться с течением времени.

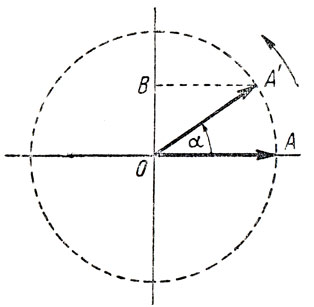Рис. 124. Вращение вектора вокруг оси

Угловая скорость, или угловая частота ω (омега), вращения равна углу поворота вектора в единицу времени:

ω = α/_t.

Следовательно, угол поворота вектора

α = ωt.

Часто вместо градуса пользуются другой единицей измерения угла — радианом. Радианом называется угол, дуга которого равна радиусу. Так как длина окружности С = 2πR, то полному углу 360° соответствует 2πR/_R = 2π радиан.

За один оборот радиус-вектор ОА будет иметь один период вращения продолжительностью Т сек.

Угловая частота в этом случае выразится так:

ω = α/_t = 2π/_Tрад/_сек.

Так как 1/_T = f, то ω = 2πf рад/_сек.

Угол поворота радиуса-вектора α от начального положения будет равен

α = ωt = 2πft.

Угол α называется фазным углом, или фазой.

Проекция вектора ОА на вертикальный диаметр равна произведению величины вектора на синус фазного угла, т. е.

OB = OA sin α.

Следовательно, проекция вращающегося вектора ОА на вертикальный диаметр изменяется по закону синуса. Если длина вектора будет А_m, то мгновенное значение проекции а равно

а = А_m sin α = А_m sin ωt;

при α = 0° величина а = А_m sin 0° = 0;

при α = 90° величина а = А_m sin 90° = А_m.

В последнем случае мгновенное значение проекции равно ее амплитудному или максимальному значению.

Задаваясь величиной фазного угла и проектируя вектор А_m на вертикальный диаметр, будем получать мгновенное значение синусоидальной величины.

Таким образом, синусоидальная величина изображается вращающимся вектором; длина вектора в масштабе выражает амплитуду синусоиды.

Проведем горизонтальную ось, на которой отложим фазные углы, проходимые вектором при его вращении (рис. 125). Откладываем затем вертикальные отрезки, равные соответствующим значениям проекции вращающегося вектора. Соединяя концы вертикальных отрезков плавной кривой, получим знакомую нам кривую — синусоиду.

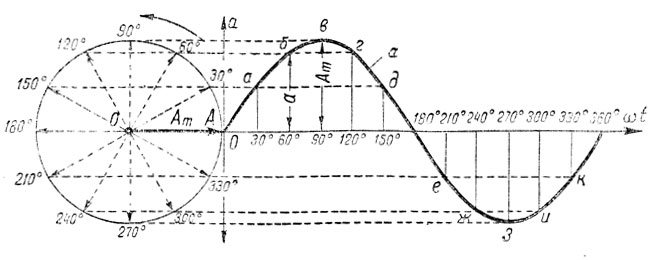Рис. 125. Получение синусоиды путем вращения вектора

Способ изображения синусоидально изменяющихся величин с помощью векторов определенной длины и определенным образом расположенных друг относительно друга называется векторной диаграммой.

Та же зависимость может быть выражена в виде синусоидальных кривых.

Таким образом, переменную синусоидальную величину можно представить тремя способами: уравнением, векторной диаграммой и графиком синусоиды.

Если радиус-вектор в начальный момент отсчета времени (t = 0) составляет некоторый угол ψ с горизонтальной осью, то в этом случае мгновенное значение переменной величины будет:

а = A_m sin (ωt + ψ).

Угол ψ (пси) называется начальным фазным углом, или начальной фазой.

Векторная диаграмма и график для этого случая даны на рис. 126.

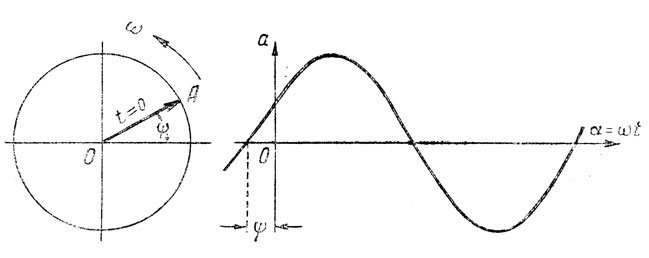Рис. 126. Построение синусоиды при наличии начальной фазы

Мы не внесем ничего нового, если будем вращать одновременно и с одинаковой скоростью ω два вектора, совпадающие по направлению. В определенный момент времени оба вектора будут повернуты на один и тот же фазный угол. Поэтому как сами векторы, так и переменные величины, которые они выражают, называют совпадающими по фазе. Векторная диаграмма и график двух величин, совпадающих по фазе, даны на рис. 127.

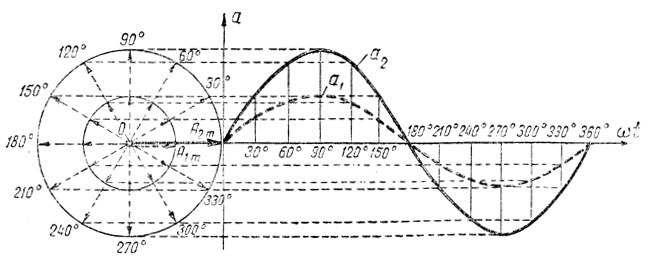Рис. 127. Построение двух синусоид путем вращения двух совпадающих векторов

Уравнения для таких величин запишутся так:

a₁ = A_1m sin ωt;
а₂ = А_2m sin ωt.

Если векторы сдвинуть один относительно другого на определенный угол а и вращать их вокруг точки О, то мы получим две синусоидальные кривые, сдвинутые, как говорят, по фазе между собой на тот же угол α. На рис. 128 показано построение двух синусоид, сдвинутых по фазе на угол а, равный 90°. В этом случае о кривой а₁ говорят, что она опережает кривую а₂ по фазе на 90°, или, наоборот, кривая а₂ отстает по фазе от кривой а₁ на 90°.

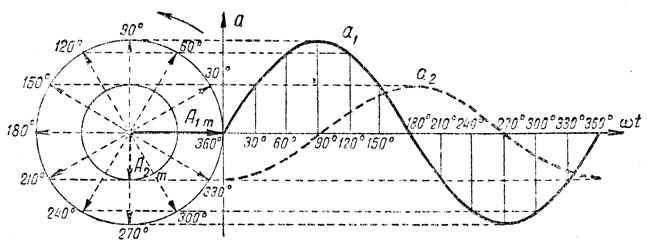Рис. 128. Построение двух синусоид, сдвинутых на 90°, путем вращения двух векторов, расположенных под углом 90°