Округление чисел

Округление десятичных чисел

Чтобы «обрезать» десятичное число, используются методы toFixed() или toPrecision(). Они оба принимают один аргумент, который определяет количество значимых и знаков после запятой, которые должны быть включены в результат:

• если для toFixed() аргумент не определен, значение по умолчанию равно , то есть без знаков после запятой; максимальное значение аргумента равно 20;
• если для toPrecision() аргумент не задан, число не изменяется.

var randNum = 6.25;
randNum.toFixed();
> "6"

Math.PI.toPrecision(1);
> "3"

var randNum = 87.335;
randNum.toFixed(2);
> "87.33"

var randNum = 87.337;
randNum.toPrecision(3);
> "87.3"

Примечание

И toFixed(), и toPrecision возвращают округленное строчное представление результата, а не число. Это означает, что прибавление rounded к randNum в результате даст конкатенацию строк, а не одно число:

console.log(randNum + rounded);
> "6.256"

Если нужно получить в результате JavaScript округление до сотых, используйте parseFloat():

var randNum = 6.25;
var rounded = parseFloat(randNum.toFixed(1));
console.log(rounded);
> 6.3

toFixed() и toPrecision() также являются полезными методами для усечения большого количества знаков после запятой. Это удобно при работе с числами, представляющими денежные единицы:

var wholeNum = 1
var dollarsCents = wholeNum.toFixed(2);
console.log(dollarsCents);
> "1.00"

Обратите внимание, что если в числе больше знаков, чем задано параметром точности, toPrecision будет выдавать результат в научном формате:

var num = 123.435
num.toPrecision(2);
> "1.2e+2"

Способы округления чисел

Для округления чисел придумано много способов, они не лишены недостатков, однако часто используются для решения задач. Разберёмся в тонкостях каждого из них.

Если используется стандартная библиотека math, то в начале кода её необходимо подключить. Сделать это можно, например, с помощью инструкции: .

math.ceil() — округление чисел в большую сторону

Функция получила своё имя от термина «ceiling», который используется в математике для описания числа, которое больше или равно заданному.

Любая дробь находится в целочисленном интервале, например, 1.2 лежит между 1 и 2. Функция определяет, какая из границ интервала наибольшая и записывает её в результат округления.

Пример:

math.ceil(5.15) # = 6
math.ceil(6.666) # = 7
math.ceil(5) # = 5

Важно помнить, что функция определяет наибольшее число с учётом знака. То есть результатом округления числа -0.9 будет 0, а не -1.

math.floor() — округление чисел в меньшую сторону

Функция округляет дробное число до ближайшего целого, которое меньше или равно исходному. Работает аналогично функции , но с округлением в противоположную сторону.

Пример:

math.floor(7.9) # = 7
math.floor(9.999) # = 9
math.floor(-6.1) # = -7

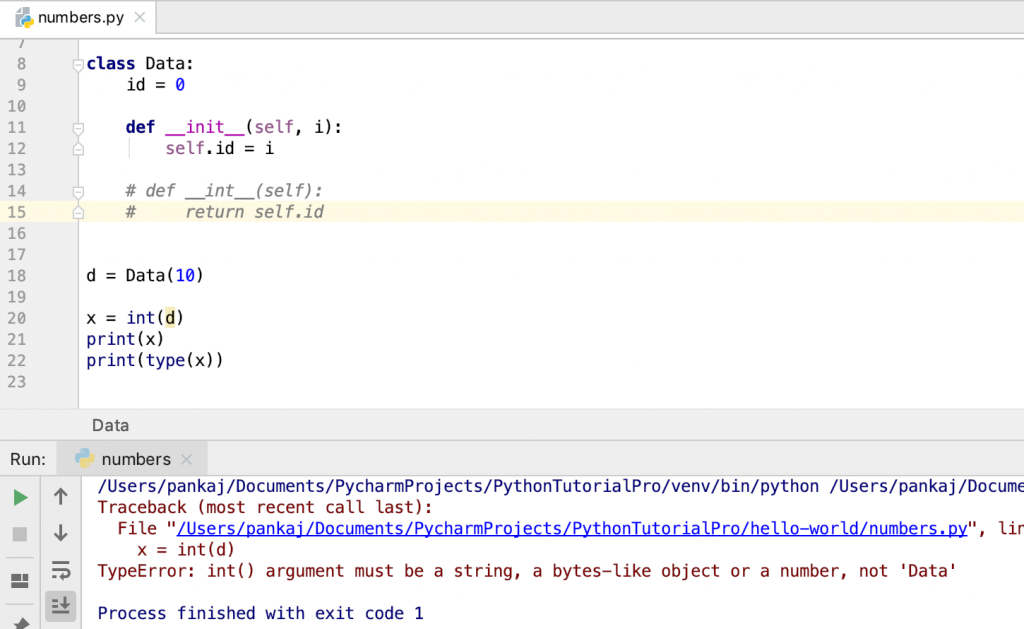
math.trunc() — отбрасывание дробной части

Возвращает целое число, не учитывая его дробную часть. То есть никакого округления не происходит, Python просто забывает о дробной части, приводя число к целочисленному виду.

Примеры:

math.trunc(5.51) # = 5
math.trunc(-6.99) # = -6

Избавиться от дробной части можно с помощью обычного преобразования числа к типу int. Такой способ полностью эквивалентен использованию .

Примеры:

int(5.51) # = 5
int(-6.99) # = -6

Нормальное округление

Python позволяет реализовать нормальное арифметическое округление, использовав функцию преобразования к типу int.

И хотя работает по другому алгоритму, результат её использования для положительных чисел полностью аналогичен выводу функции floor(), которая округляет числа «вниз». Для отрицательных аналогичен функции ceil().

Примеры:

math.floor(9.999) # = 9
int(9.999) # = 9
math.ceil(-9.999) # = -9
int(-9.999) # = -9

Чтобы с помощью функции int() округлить число по математическим правилам, необходимо добавить к нему 0.5, если оно положительное, и -0.5, если оно отрицательное.

Тогда операция принимает такой вид: int(num + (0.5 if num > 0 else -0.5)). Чтобы каждый раз не писать условие, удобно сделать отдельную функцию:

def int_r(num):
    num = int(num + (0.5 if num > 0 else -0.5))
    return num

Функция работает также, как стандартная функция округление во второй версии Python (арифметическое округление).

Примеры:

int_r(11.5) # = 12
int_r(11.4) # = 11
int_r(-0.991) # = -1
int_r(1.391) # = 1

round() — округление чисел

round() — стандартная функция округления в языке Python. Она не всегда работает так, как ожидается, а её алгоритм различается в разных версиях Python.

В Python 2

Во второй версии Python используется арифметическое округление. Оно обладает постоянно растущей погрешностью, что приводит к появлению неточностей и ошибок.

Увеличение погрешности вызвано неравным количеством цифр, определяющих, в какую сторону округлять. Всего 4 цифры на конце приводят к округлению «вниз», и 5 цифр к округлению «вверх».

Помимо этого, могут быть неточности, например, если округлить число 2.675 до второго знака, получится число 2.67 вместо 2.68. Это происходит из-за невозможности точно представить десятичные числа типа «float» в двоичном коде.

В Python 3

В третьей версии Python используется банковское округление. Это значит, что округление происходит до самого близкого чётного.

Такой подход не избавляет от ошибок полностью, но уменьшает шанс их возникновения и позволяет программисту добиться большей точности при вычислениях.

Примеры:

round(3.5) # = 4
round(9.5) # = 10
round(6.5) # = 6
round(-6.5) # = -6
round(-7.5) # = -8

Но если вам по каким то причинам нужно округление как в Python 2, то можно воспользоваться функцией написанной нами выше на основе приведения к целому числу.

Округление до сотых

У функции есть ещё один аргумент. Он показывает до какого количества знаков после запятой следует округлять. Таким образом, если нам надо в Python округлить до сотых, этому параметру следует задать значение 2.

Пример округления до нужного знака:

round(3.555, 2) # = 3.56
round(9.515,1) # = 9.5
round(6.657,2) # = 6.66

Калькулятор расчета мощности кондиционера по площади комнаты в Excel

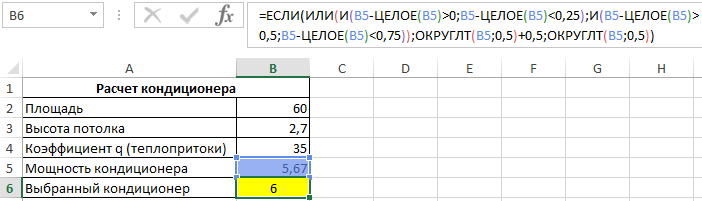
Пример 3. Для помещения площадью 60 кв. м и высотой потолка 2,7 м необходимо подобрать кондиционер по мощности. Поставщики предлагают кондиционеры мощностью от 2 кВт с шагом 0,5 кВт. Определить подходящий кондиционер.

Таблица данных:

Искомая мощность рассчитывается как произведение площади, высоты потолка и коэффициента q. Используем следующую формулу:

=B2*B3*B4/1000

Для автоматического выбора кондиционера используем формулу:

В данном случае функция ЕСЛИ выполняет проверку дробной части найденного значения мощности на принадлежность к промежутку значений от 0 до 0,25 и от 0,5 до 0,75. Это необходимо для правильного выбора кондиционера по мощности. Например, если бы результатом расчетов являлась мощность 5,2 кВт, функция ОКРУГЛТ(5,2;0,5) вернула бы значение 5. Однако мощность выбранного кондиционера должна быть равной или больше расчетной. Поэтому в этом случае к результату будет добавлено значение 0,5.

Результат расчета мощности кондиционера по площади комнаты:

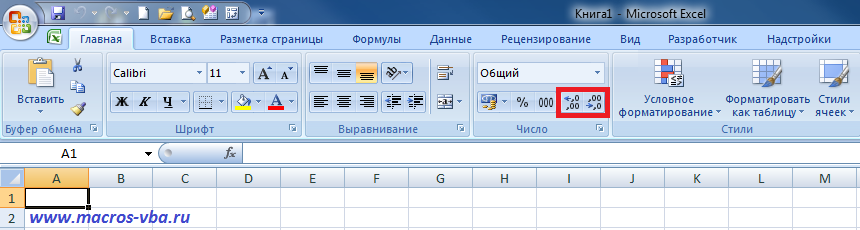
Настройка отображения чисел через панель инструментов

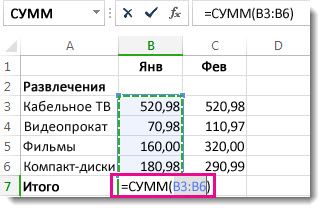
Самый простой способ округлить число, а точнее, его отображения на экране – через кнопки на Панели инструментов. Чтобы найти их, должна быть открыта вкладка “Главная”, в которой расположен подраздел “Число”. Здесь и находятся требуемые функции “Увеличить разрядность” или “Уменьшить разрядность”.

Выберите ячейку с числом и нажмите на кнопку с нужным действием. Функция “Увеличить разрядность” будет добавлять в конец дробной части нули.

Функция “Уменьшить разрядность” будет убирать цифры с конца, округляя окончания.

Примечание: Важно помнить, что числовое значение, которое хранится в памяти программы после проделанных действий никак не изменится, и расчеты будут производиться с исходным значением

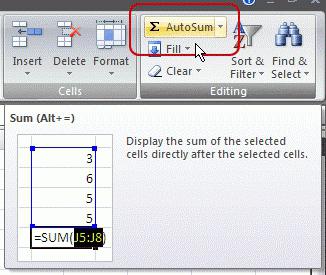
Как округлить с помощью функции Excel?

А теперь перейдем непосредственно к практике. Что нужно делать, чтобы осуществить округление чисел с помощью функции? Для этого существует специальная функция ОКРУГЛ. Ее можно вызвать разными способами: через ленту в Excel 2007 версии и более новые.

Второй способ – написать вручную. Он более продвинутый, потому что нужно как минимум знать синтаксис.

Наиболее простой для новичка метод – воспользоваться мастером функций. Чтобы это сделать, нужно найти возле строки ввода формулы кнопочку, на которой написана комбинация маленьких буковок fx. Найти эту функцию можно в разделе «Математические», и после ее выбора будет предложено ввести аргументы. Каждый из них подписан, поэтому разобраться несложно.

Синтаксис функции ОКРУГЛ

Если используется ручной ввод, то нужно понимать, как правильно записывать формулу. Последовательность ввода значений называется синтаксисом. Любая функция имеет универсальный общий синтаксис. Сначала записывается знак равно, потом название функции, потом аргументы, которые прописываются в скобках, а разделяются между собой запятой. Количество аргументов может отличаться от функции к функции. В некоторых их вообще нет, а в ряде из них их хоть 5, хоть больше. 

В случае с функцией ОКРУГЛ их два. Давайте рассмотрим их более подробно.

Аргументы функции ОКРУГЛ

Итак, функция предусматривает два аргумента:

1. Число. Сюда указывается ссылка на ячейку. Или же можно ввести требуемое значение в этот аргумент вручную.

2. Количество знаков, на какое собираетесь осуществить округление.

Чтобы округлить целое число (то есть, которое не имеет ни одного знака после запятой), просто напишите знак минуса перед числом во втором параметре. Для округления до десятков, необходимо написать -1, до сотен – -2, и по такой логике далее. Чем больше модуль этого числа, тем на большее количество цифр будет осуществляться округление. 

Основы использования функции ОКРУГЛ

Давайте рассмотрим то как можно использовать эту функцию, на примере округления до тысяч.

Представим, у нас открылась такая таблица. Мы во вторую ячейку прописали формулу округления, и результат видим на этом скриншоте.

4

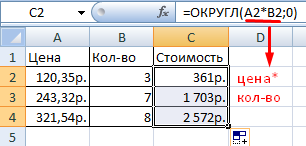
Возможно округление не только числа, но и любого значения. На примере это выглядит так. Представим, что у нас есть три столбца. В первом записывается цена товара, во втором – сколько его было куплено. Но и в третьем, соответственно, указывается итоговая стоимость. 

Представим, что наша задача – показывать сумму в рублях, а копейки игнорировать. Тогда получится следующая таблица.

5

По кратности

Excel дает возможность осуществлять округление чисел не до самого ближнего, а до того, которое является кратным по отношению к определенному. Для этого существует специальная функция, которая называется ОКРУГЛТ. С ее помощью можно добиться необходимой точности округления. 

Основных аргумента два. Первое – это непосредственно число, которое нужно округлить. Второй – это число, которому должно быть кратное заданное. Оба аргумента можно передавать как вручную, так и через ячейку. 

По количеству знаков

Все описанные выше примеры – это частные случаи округления по количеству знаков. Достаточно просто ввести в соответствующем аргументе функции необходимое количество знаков, которое нужно оставить. Собственно, это и все. 

Как грамотно округлить число в Excel

В нашем случае округление было осуществлено в сторону увеличения. Это зависит от числа, которое убирается. Если перед нужным значением находится 5 или больше, то округление осуществляется в направлении увеличения, а если меньше – уменьшения. Все так, как нужно делать в математике, никаких изменений в правилах нет.

Точность результата зависит от того, сколько знаков в дробной части человек решил оставить. Чем оно больше, тем выше точность. Поэтому настоятельно рекомендуется выполнять округление значений лишь в тех ситуациях, когда в этом есть реальная практическая необходимость. Иногда даже малейшее округление может абсолютно исказить расчеты. Это, кстати, одна из наиболее распространенных причин, почему так часто синоптики ошибаются. Даже был открыт эффект бабочки, когда из-за незначительных различий между округленным значением и настоящим был спрогнозирован дождливый сезон.

Примечания

1. ↑
2. Кнут Д. Э. Искусство программирования. Том 1. Основные алгоритмы = The Art of Computer Programming. Volume 1. Fundamental Algorithms / под ред. С. Г. Тригуб (гл. 1), Ю. Г. Гордиенко (гл. 2) и И. В. Красикова (разд. 2.5 и 2.6). — 3. — Москва: Вильямс, 2002. — Т. 1. — 720 с. — ISBN 5-8459-0080-8.
3. A’HEARN, B., J. BATEN AND D. CRAYEN (2009). “Quantifying Quantitative Literacy: Age Heaping and the History of Human Capital”, Journal of Economic History 69,783-808.
4. В. М. Заварыкин, В. Г. Житомирский, М. П. Лапчик. Техника вычислений и алгоритмизация: Вводный курс: Учебное пособие для студентов педагогических институтов по физико-математическим специальностям. — М: Просвещение, 1987. 160 с.: ил.
5. цит. по В. Гильде, З. Альтрихтер. «С микрокалькулятором в руках». Издание второе. Перевод с немецкого Ю. А. Данилова. М:Мир, 1987, стр. 64.

Правила округления чисел

Согласно правилу округления нужно решить, до какого числа округляется значение. После этого нужно посмотреть на цифру, которая стоит после выбранной:

• Если цифра равняется или больше 5, то значащее значение округляют с увеличением на 1.
• Если цифра меньше 5, то значение округляют без увеличения.

Рассмотрим пример округления числа после запятой. Сначала округлим до сотых число 1,235. После позиции сотых, на позиции тысячных находится число 5, значит, при округлении добавляем к сотым 1. Значит, если округлить 1,235, то получится 1,24.

Чем меньше число, до которого округляется результат, тем выше точность после округления. Можно округлять даже до десятков и сотен, однако, результаты таких округлений оставляют желать лучшего. Поэтому в большей части вычислений и округляют до сотых.

Что мы узнали?

Мы поговорили о правилах округления чисел после запятой. Узнали, как правильно округлять числа, а также рассказали, как округления влияют на точность числа. Сказали, до каких чисел округляются значения в рядовых математических вычислениях.

1. Вопрос 1 из 5

Начать тест(новая вкладка)

Получение приближенных значений

Это математическое действие осуществляется по определенным правилам.

Но для каждого множества чисел они разные. Отмечают, что округлить можно целые числа и десятичные дроби.

А вот с обыкновенными дробями действие не выполняется.

Сначала их необходимо перевести в десятичные дроби, а затем приступить к процедуре в необходимом контексте.

Правила приближения значений заключаются в следующем:

• для целых – замена разрядов, следующих за округляемым, нулями,
• для десятичных дробей – отбрасывания всех чисел, которые находятся за округляемым разрядом.

К примеру, округляя 303 434 до тысяч, необходимо заменить сотни, десятки и единицы нулями, то есть 303 000. В десятичных дробях 3,3333 округляя до десятых, просто отбрасывают все последующие цифры и получают результат 3,3.

Эмпирические правила арифметики с округлениями

В тех случаях, когда нет необходимости в точном учёте вычислительных погрешностей, а требуется лишь приблизительно оценить количество точных цифр в результате расчёта по формуле, можно пользоваться набором простых правил округлённых вычислений:

Все исходные значения округляются до реальной точности измерений и записываются с соответствующим числом значащих цифр, так, чтобы в десятичной записи все цифры были надёжными (допускается, чтобы последняя цифра была сомнительной). При необходимости значения записываются со значащими правыми нулями, чтобы в записи указывалось реальное число надёжных знаков (например, если длина в 1 м реально измерена с точностью до сантиметров, записывается «1,00 м», чтобы было видно, что в записи надёжны два знака после запятой), или точность явно указывается (например, 2500±5 м — здесь надёжными являются только десятки, до них и следует округлять).
Промежуточные значения округляются с одной «запасной» цифрой.
При сложении и вычитании результат округляется до последнего десятичного знака наименее точного из параметров (например, при вычислении значения 1,00 м + 1,5 м + 0,075 м результат округляется до десятых метра, то есть до 2,6 м). При этом рекомендуется выполнять вычисления в таком порядке, чтобы избегать вычитания близких по величине чисел и производить действия над числами по возможности в порядке возрастания их модулей.
При умножении и делении результат округляется до наименьшего числа значащих цифр, которое имеют множители или делимое и делитель

Например, если тело при равномерном движении прошло дистанцию 2,5 × 103 метров за 635 секунд, то при вычислении скорости результат должен быть округлён до 3,9 м/с, поскольку одно из чисел (расстояние) известно лишь с точностью до двух значащих цифр.

Важное замечание: если один операндов при умножении или делитель при делении является по смыслу целым числом (то есть не результатом измерений непрерывной физической величины с точностью до целых единиц, а, например, количеством или просто целой константой), то количество значащих цифр в нём на точность результата операции не влияет, и оставляемое число цифр определяется только вторым операндом. Например, кинетическая энергия тела массой 0,325 кг, движущегося со скоростью 5,2 м/с, равна Ek=mv22=0.325⋅5.222=4.394≈4.4{\displaystyle E_{k}={\tfrac {mv^{2}}{2}}={\tfrac {0.325\cdot 5.2^{2}}{2}}=4.394\approx 4.4} Дж — округляется до двух знаков (по количеству значащих цифр в значении скорости), а не до одного (делитель 2 в формуле), так как значение 2 по смыслу — целая константа формулы, она является абсолютно точной и не влияет на точность вычислений (формально такой операнд можно считать «измеренным с бесконечным числом значащих цифр»).

При вычислении значения функции f(x){\displaystyle f\left(x\right)} требуется оценить значение модуля производной этой функции в окрестности точки вычисления

Если |f′(x)|⩽1{\displaystyle \left|f’\left(x\right)\right|\leqslant 1}, то результат функции точен до того же десятичного разряда, что и аргумент. В противном случае результат содержит меньше точных десятичных разрядов на величину log10⁡(|f′(x)|){\displaystyle \log _{10}\left(\left|f’\left(x\right)\right|\right)}, округлённую до целого в большую сторону.

Несмотря на нестрогость, приведённые правила достаточно хорошо работают на практике, в частности, из-за достаточно высокой вероятности взаимопогашения ошибок, которая при точном учёте погрешностей обычно не учитывается.

Варианты округления 0,5 к ближайшему целому

Отдельного описания требуют правила округления для специального случая, когда (N+1)-й знак = 5, а последующие знаки равны нулю. Если во всех остальных случаях округление до ближайшего целого обеспечивает меньшую погрешность округления, то данный частный случай характерен тем, что для однократного округления формально безразлично, производить его «вверх» или «вниз» — в обоих случаях вносится погрешность ровно в 1/2 младшего разряда. Существуют следующие варианты правила округления до ближайшего целого для данного случая:

• Математическое округление — округление всегда в бо́льшую по модулю сторону (предыдущий разряд всегда увеличивается на единицу).
• Банковское округление (англ. banker’s rounding) — округление для этого случая происходит к ближайшему чётному, то есть 2,5 → 2; 3,5 → 4.
• Случайное округление — округление происходит в меньшую или большую сторону в случайном порядке, но с равной вероятностью (может использоваться в статистике). Также часто используется округление с неравными вероятностями (вероятность округления вверх равна дробной части), этот способ делает накопление ошибок случайной величиной с нулевым математическим ожиданием.
• Чередующееся округление — округление происходит в меньшую или большую сторону поочерёдно.

Во всех вариантах в случае, когда (N+1)-й знак не равен 5 или последующие знаки не равны нулю, округление происходит по обычным правилам: 2,49 → 2; 2,51 → 3.

Математическое округление просто формально соответствует общему правилу округления (см. выше). Его недостатком является то, что при округлении большого числа значений, которые далее будут обрабатываться совместно, может происходить накопление ошибки округления. Типичный пример: округление до целых рублей денежных сумм, выражаемых в рублях и копейках. В реестре из 10 000 строк (если считать копеечную часть каждой суммы случайным числом с равномерным распределением, что обычно вполне допустимо) окажется в среднем около 100 строк с суммами, содержащими в части копеек значение 50. При округлении всех таких строк по правилам математического округления «вверх» сумма «итого» по округлённому реестру окажется на 50 рублей больше точной.

Три остальных варианта как раз и придуманы для того, чтобы уменьшить общую погрешность суммы при округлении большого количества значений. Округление «до ближайшего чётного» исходит из предположения, что при большом числе округляемых значений, имеющих 0,5 в округляемом остатке, в среднем половина из них окажется слева, а половина — справа от ближайшего чётного, таким образом, ошибки округления взаимно погасятся. Строго говоря, предположение это верно лишь тогда, когда набор округляемых чисел обладает свойствами случайного ряда, что обычно верно в бухгалтерских приложениях, где речь идёт о ценах, суммах на счетах и так далее. Если же предположение будет нарушено, то и округление «до чётного» может приводить к систематическим ошибкам. Для таких случаев лучше работают два следующих метода.

Два последних варианта округления гарантируют, что примерно половина специальных значений будет округлена в одну сторону, половина — в другую. Но реализация таких методов на практике требует дополнительных усилий по организации вычислительного процесса.

• Округление в случайную сторону требует для каждой округляемой строки генерировать случайное число. При использовании псевдослучайных чисел, создаваемых линейным реккурентным методом, для генерации каждого числа требуется операция умножения, сложения и деления по модулю, что для больших объёмов данных может существенно замедлить расчёты.
• Чередующееся округление требует хранить флаг, показывающий, в какую сторону последний раз округлялось специальное значение, и при каждой операции переключать значение этого флага.

Как округлять числа

Натуральные числа

Все числа, в которых больше одного знака, имеют разряды. Это место, на котором в числе стоит та или иная цифра. Например, в числе 342 три разряда: сотен (три сотни), десятков (четыре десятка) и единиц (две единицы). Соответственно, округлять числа можно до десятков, сотен, тысяч и так далее.

При округлении цифры в ненужных нам разрядах заменяются нулями (по сути, отбрасываются), а цифра в нужном разряде либо изменяется в большую сторону, либо остаётся неизменной. Это зависит от того, какая цифра стоит за ней. Если от 0 до 4, то ничего не происходит. Если от 5 до 9, тогда к разряду прибавляется единица.

Возьмём число 21 769. Его можно округлить следующим образом:

• До десятков. Находим количество десятков в числе 21 769 — их шесть. За шестёркой стоит цифра 9, значит, при округлении разряд десятков увеличится на один. То есть ответ — 21 770.
• До сотен. Находим количество сотен в числе 21 769 — их семь. Теперь проверяем цифру за семёркой — это 6, соответственно, к разряду сотен прибавляем единицу. Результат — 21 800.
• До тысяч. Находим количество тысяч — их 21. За единицей стоит семёрка, значит, при округлении числа разряд тысяч увеличиваем на один и получаем 22 000.

Дробные числа

При округлении дробей действуют точно такие же правила, как и при округлении натуральных чисел. Только нужно быть более внимательным, потому что разрядов в дробях больше — они есть и в целой части (единицы, десятки, сотни, тысячи и т. д.), и в дробной (десятые, сотые, тысячные и т. д.).

Например, возьмём десятичную дробь 45,836. Её можно округлить так:

• до сотых → 45,84;
• до десятых → 45,8;
• до целого → 46;
• до десятков → 50.

Округление натуральных чисел

Натуральные числа — это числа, которые мы используем, чтобы посчитать что-то конкретное, осязаемое. Вот они: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13 и так далее.

Особенности натуральных чисел:

• Наименьшее натуральное число: единица (1).
• Наибольшего натурального числа не существует. Натуральный ряд бесконечен.
• У натурального ряда каждое следующее число больше предыдущего на единицу: 1, 2, 3, 4, 5, 6, 7.

Округление натурального числа — это замена его таким ближайшим по значению числом, у которого одна или несколько последних цифр в его записи заменены нулями.

Чтобы округлить натуральное число, нужно в записи числа выбрать разряд, до которого производится округление.

Правила округления чисел:

1. Подчеркнуть цифру разряда, до которого надо округлить число.
2. Отделить все цифры справа от этого разряда вертикальной чертой.
3. Если справа от подчеркнутой цифры стоит 0,1, 2, 3 или 4 — все цифры, которые отделены справа, заменяем нулями. Цифру разряда, до которой округляли, оставляем без изменений.
4. Если справа от подчеркнутой цифры стоит 5, 6, 7, 8 или 9 — все цифры, которые отделены справа, заменяем нулями. К цифре разряда, до которой округляли, прибавляем 1.

Давайте рассмотрим, как округлить число 57 861 до тысяч. Выполним первые два пункта из правил округления.

После подчеркнутой цифры стоит 8, значит к цифре разряда тысяч (в данном случае 7) прибавим 1. На месте цифр, отделенных вертикальной чертой, ставим нули.

Теперь округлим 756 485 до сотен:

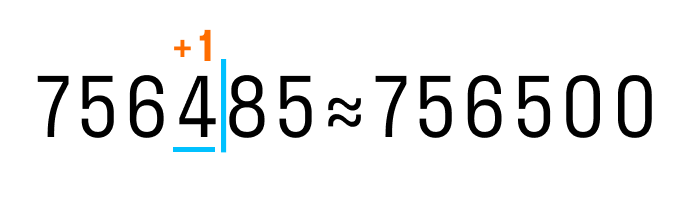
Округлим число 123 до десятков: 123 ≈ 120.

Округлим число 3581 до сотен: 3581 ≈ 3580.

Если в разряде, до которого производится округление, стоит цифра 9 и необходимо ее увеличить на единицу — в этом разряде записывается цифра 0, а цифра слева в соседнем старшем разряде увеличивается на 1.

Примеры:

• как округлить число 697 до десятков — 697 ≈ 700;
• как округлить число 980 до сотен — 980 ≈ 1000.

Иногда уместно записать округленный результат с сокращениями «тыс.» (тысяча), «млн.» (миллион) и «млрд.» (миллиард). Вот так:

• 7 882 000 = 7 882 тыс.
• 1 000 000 = 1 млн.

Правило встречается в следующих упражнениях:

5 класс

Задание 1274,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Задание 1275,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Задание 1324,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Задание 1368,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Задание 1411,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Задание 1524,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Номер 856,
Мерзляк, Полонский, Якир, Учебник

Номер 857,
Мерзляк, Полонский, Якир, Учебник

Номер 5,
Мерзляк, Полонский, Якир, Учебник

Номер 922,
Мерзляк, Полонский, Якир, Учебник

6 класс

Номер 1,
Мерзляк, Полонский, Якир, Учебник

Задание 236,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Задание 628,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Задание 629,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Задание 645,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Задание 876,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Задание 1198,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Задание 1223,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Задание 1504,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Задание 1580,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Как округлить число до тысячных

Правило округления числа до тысячных

Если первая из отброшенных цифр , 1, 2, 3 или 4, то предыдущую цифру не изменяем.

Если первая из отброшенных цифр 5, 6, 7, 8 или 9, то предыдущую цифру увеличиваем на единицу.

Пример кругления числа до тысячных:Чтобы округлить число до тысячных, после запятой нужно оставить лишь три цифры, а четвертую — отбросить. Поскольку отброшенная цифра — 4, предыдущую цифру оставляем без изменений. Читают: «Три целых, семь тысяч восемьсот пятьдесят четыре десятитысячных приближенно равно три целых, семьсот восемьдесят пять тысячных».Чтобы округлить это число до тысячных, после запятой оставляем три цифры, а четвертую — отбрасываем. Отброшенная цифра — 6, значит предыдущую цифру увеличиваем на единицу. Читают: «Тридцать семь целых две тысячи семьдесят шесть десятитысячных приближенно равно тридцать семь целых двести восемь тысячных».Округляя число до тысячных, оставляем после запятой три цифры, а все остальные — отбрасываем. Так как первая из отброшенных цифр — 8, к предыдущей прибавляем единицу. Читают: «Шестьдесят девять целых девяносто девять тысяч девятьсот восемьдесят одна стотысячная приближенно равно семьдесят целых нуль тысячных».Округляем число до тысячных, поэтому после запятой оставляем первые три цифры, а следующие за ними — отбрасываем. Так как первая из отброшенных цифр — 2, то предыдущую цифру не меняем. Читают: «Восемьсот шестьдесят три целых двенадцать тысяч четыреста двадцать три стотысячных приближенно равно восемьсот шестьдесят три целых сто двадцать четыре тысячных».Чтобы округлить данное число до тысячных, первые три цифры, стоящие после запятой, оставляем, а все остальные — отбрасываем. Первая из отброшенных цифр равна 5, а это означает, что предыдущую цифру следует увеличить на единицу. Читают: «Нуль целых триста пятьдесят девять стотысячных приближенно равно нуль целых четыре тысячных».

Комментарии

Поведение этого метода соответствует стандарту IEEE 754, разделу 4.The behavior of this method follows IEEE Standard 754, section 4. Этот тип округления иногда называют округлением в сторону отрицательной бесконечности.This kind of rounding is sometimes called rounding toward negative infinity.

Floor(Double)

Возвращает наибольшее целое число, которое меньше или равно заданному числу с плавающей запятой двойной точности.Returns the largest integral value less than or equal to the specified double-precision floating-point number.

d

Double

Число двойной точности с плавающей запятой.A double-precision floating-point number.

Возвращаемое значение

Double

Наибольшее целое число, которое меньше или равно .The largest integral value less than or equal to . Если значение параметра равно NaN, NegativeInfinity или PositiveInfinity, возвращается это значение.If is equal to NaN, NegativeInfinity, or PositiveInfinity, that value is returned.

Примеры

В следующем примере показан метод и его отличие от метода.The following example illustrates the method and contrasts it with the method.

Комментарии

Поведение этого метода соответствует стандарту IEEE 754, разделу 4.The behavior of this method follows IEEE Standard 754, section 4. Этот тип округления иногда называют округлением в сторону отрицательной бесконечности.This kind of rounding is sometimes called rounding toward negative infinity. Иными словами, если является положительным, любой дробный компонент усекается.In other words, if is positive, any fractional component is truncated. Если имеет отрицательное значение, присутствие любого компонента дробной части приводит к округлению его до меньшего целого числа.If is negative, the presence of any fractional component causes it to be rounded to the smaller integer. Операция этого метода отличается от Ceiling метода, который поддерживает округление в сторону положительной бесконечности.The operation of this method differs from the Ceiling method, which supports rounding toward positive infinity.

Начиная с Visual Basic 15,8, производительность преобразования типа «двойное в целое число» оптимизирована, если передать значение, возвращаемое методом, в любую функцию целочисленного преобразованияили если значение Double, возвращаемое, автоматически преобразуется в целое число с параметром Option-on , равным OFF.Starting with Visual Basic 15.8, the performance of Double-to-integer conversion is optimized if you pass the value returned by the method to the any of the integral conversion functions, or if the Double value returned by is automatically converted to an integer with Option Strict set to Off. Эта оптимизация позволяет коду выполняться быстрее — до двух раз быстрее для кода, который выполняет большое количество преобразований в целочисленные типы.This optimization allows code to run faster — up to twice as fast for code that does a large number of conversions to integer types. В следующем примере показаны оптимизированные преобразования:The following example illustrates such optimized conversions: