Нюансы работы с вещественными числами

Формат ячейки

Самый простой способ округления – настройка отображения цифр в ячейке. Для этого необходимо сделать следующее:

1. Заполняете рабочий лист необходимыми данными.

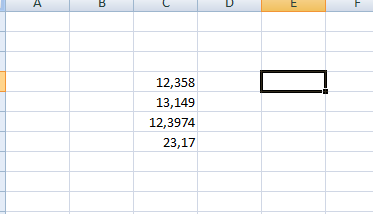
1. Щелкаете по нужной ячейке правой клавишей мыши и ищете строку Формат ячеек….

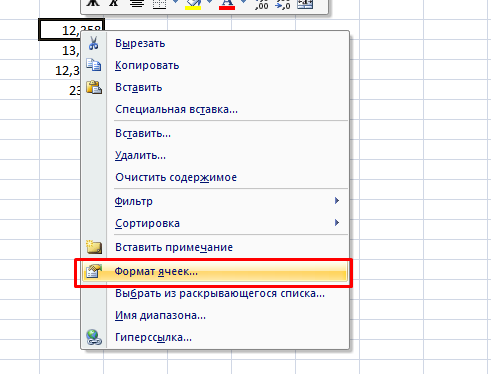
1. В появившемся окне на первой вкладке выбираете Числовой формат отображения, затем в блоке справа изменяете число десятичных знаков, при этом ниже можно сразу же увидеть результаты форматирования. Подтверждаете действие нажатием клавиши ОК.

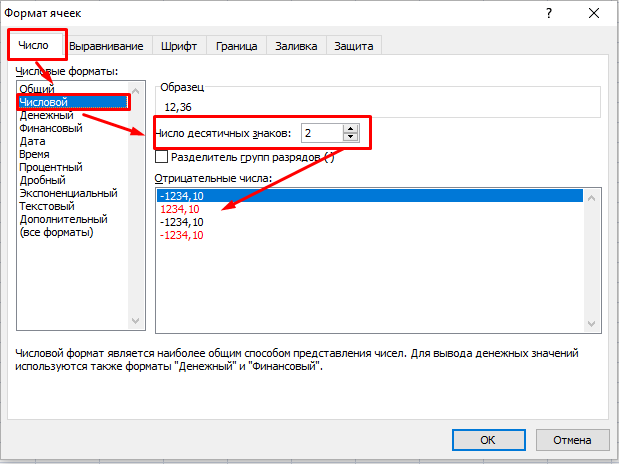
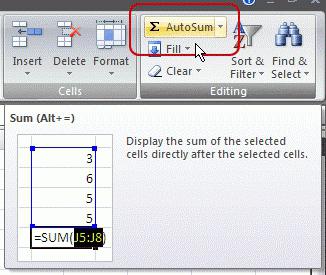
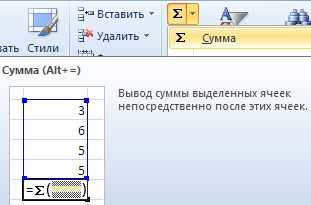
Быстрее эту операцию можно провести, используя специальные кнопки в блоке Число во вкладке Главная на Панели инструментов.

Недостатком этого метода является то, что округления не происходит, а изменяется лишь внешний вид числа. Для дальнейшего использования такая цифра не подходит, поскольку в расчетах будут использоваться все знаки после запятой.

Комментарии

Поведение этого метода соответствует стандарту IEEE 754, разделу 4.The behavior of this method follows IEEE Standard 754, section 4. Этот тип округления иногда называют округлением в сторону отрицательной бесконечности.This kind of rounding is sometimes called rounding toward negative infinity.

Floor(Double)

Возвращает наибольшее целое число, которое меньше или равно заданному числу с плавающей запятой двойной точности.Returns the largest integral value less than or equal to the specified double-precision floating-point number.

d

Double

Число двойной точности с плавающей запятой.A double-precision floating-point number.

Возвращаемое значение

Double

Наибольшее целое число, которое меньше или равно .The largest integral value less than or equal to . Если значение параметра равно NaN, NegativeInfinity или PositiveInfinity, возвращается это значение.If is equal to NaN, NegativeInfinity, or PositiveInfinity, that value is returned.

Примеры

В следующем примере показан метод и его отличие от метода.The following example illustrates the method and contrasts it with the method.

Комментарии

Поведение этого метода соответствует стандарту IEEE 754, разделу 4.The behavior of this method follows IEEE Standard 754, section 4. Этот тип округления иногда называют округлением в сторону отрицательной бесконечности.This kind of rounding is sometimes called rounding toward negative infinity. Иными словами, если является положительным, любой дробный компонент усекается.In other words, if is positive, any fractional component is truncated. Если имеет отрицательное значение, присутствие любого компонента дробной части приводит к округлению его до меньшего целого числа.If is negative, the presence of any fractional component causes it to be rounded to the smaller integer. Операция этого метода отличается от Ceiling метода, который поддерживает округление в сторону положительной бесконечности.The operation of this method differs from the Ceiling method, which supports rounding toward positive infinity.

Начиная с Visual Basic 15,8, производительность преобразования типа «двойное в целое число» оптимизирована, если передать значение, возвращаемое методом, в любую функцию целочисленного преобразованияили если значение Double, возвращаемое, автоматически преобразуется в целое число с параметром Option-on , равным OFF.Starting with Visual Basic 15.8, the performance of Double-to-integer conversion is optimized if you pass the value returned by the method to the any of the integral conversion functions, or if the Double value returned by is automatically converted to an integer with Option Strict set to Off. Эта оптимизация позволяет коду выполняться быстрее — до двух раз быстрее для кода, который выполняет большое количество преобразований в целочисленные типы.This optimization allows code to run faster — up to twice as fast for code that does a large number of conversions to integer types. В следующем примере показаны оптимизированные преобразования:The following example illustrates such optimized conversions:

Особенности числовой арифметики

В JavaScript
число представлено в виде 64-битного формата IEEE-754. Для хранения числа
используется 64 бита: 52 из них используется для хранения цифр, 11 из них для
хранения положения десятичной точки (если число целое, то хранится 0), и один
бит отведён на хранение знака. Если число слишком большое, оно переполнит
64-битное хранилище, JavaScript вернёт бесконечность:

console.log( 1e500 ); // Infinity

Наиболее часто
встречающаяся ошибка при работе с числами в JavaScript – это потеря точности.
Например, сумма двух таких вещественных чисел:

let res = 0.1+0.2;
console.log( res );

не дает точное
значение 0,3. Потому, например, при таком сравнении:

if(res == 0.3) console.log( true );

мы получим
значение false и оператор
после if выполнен не
будет. Почему так происходит? Не вдаваясь в подробности, можно сказать так:
вещественные числа 0.1 и 0.3 в двоичной системе счисления (именно так они
представляются в памяти ЭВМ) являются бесконечной дробью. Отсюда и потеря
точности.

Использование округлений при работе с числами ограниченной точности

Реальные физические величины всегда измеряются с некоторой конечной точностью, которая зависит от приборов и методов измерения и оценивается максимальным относительным или абсолютным отклонением неизвестного истинного значения от измеренного, что в десятичном представлении значения соответствует либо определённому числу значащих цифр, либо определённой позиции в записи числа, все цифры после (правее) которой являются незначащими (лежат в пределах ошибки измерения). Сами измеренные параметры записываются с таким числом знаков, чтобы все цифры были надёжными, возможно, последняя — сомнительной. Погрешность при математических операциях с числами ограниченной точности сохраняется и изменяется по известным математическим законам, поэтому когда в дальнейших вычислениях возникают промежуточные значения и результаты с больши́м числом цифр, из этих цифр только часть являются значимыми. Остальные цифры, присутствуя в значениях, фактически не отражают никакой физической реальности и лишь отнимают время на вычисления. Вследствие этого промежуточные значения и результаты при вычислениях с ограниченной точностью округляют до того количества знаков, которое отражает реальную точность полученных значений. На практике обычно рекомендуется при длинных «цепочных» ручных вычислениях сохранять в промежуточных значениях на одну цифру больше. При использовании компьютера промежуточные округления в научно-технических приложениях чаще всего теряют смысл, и округляется только результат.

Так, например, если задана сила 5815 гс с точностью до грамма силы и длина плеча 1,4 м с точностью до сантиметра, то момент силы в кгс по формуле M=(mg)⋅h{\displaystyle M=(mg)\cdot h}, в случае формального расчёта со всеми знаками, окажется равным: 5,815 кгс • 1,4 м = 8,141 кгс•м. Однако если учесть погрешность измерения, то мы получим, что предельная относительная погрешность первого значения составляет 1/5815 ≈ 1,7•10−4, второго — 1/140 ≈ 7,1•10−3, относительная погрешность результата по правилу погрешности операции умножения (при умножении приближённых величин относительные погрешности складываются) составит 7,3•10−3, что соответствует максимальной абсолютной погрешности результата ±0,059 кгс•м! То есть в реальности, с учётом погрешности, результат может составлять от 8,082 до 8,200 кгс•м, таким образом, в рассчитанном значении 8,141 кгс•м полностью надёжной является только первая цифра, даже вторая — уже сомнительна! Корректным будет округление результата вычислений до первой сомнительной цифры, то есть до десятых: 8,1 кгс•м, или, при необходимости более точного указания рамок погрешности, представить его в виде, округлённом до одного-двух знаков после запятой с указанием погрешности: 8,14 ± 0,06 кгс•м.

JavaScript

JS Array
concat()
constructor
copyWithin()
entries()
every()
fill()
filter()
find()
findIndex()
forEach()
from()
includes()
indexOf()
isArray()
join()
keys()
length
lastIndexOf()
map()
pop()
prototype
push()
reduce()
reduceRight()
reverse()
shift()
slice()
some()
sort()
splice()
toString()
unshift()
valueOf()

JS Boolean
constructor
prototype
toString()
valueOf()

JS Classes
constructor()
extends
static
super

JS Date
constructor
getDate()
getDay()
getFullYear()
getHours()
getMilliseconds()
getMinutes()
getMonth()
getSeconds()
getTime()
getTimezoneOffset()
getUTCDate()
getUTCDay()
getUTCFullYear()
getUTCHours()
getUTCMilliseconds()
getUTCMinutes()
getUTCMonth()
getUTCSeconds()
now()
parse()
prototype
setDate()
setFullYear()
setHours()
setMilliseconds()
setMinutes()
setMonth()
setSeconds()
setTime()
setUTCDate()
setUTCFullYear()
setUTCHours()
setUTCMilliseconds()
setUTCMinutes()
setUTCMonth()
setUTCSeconds()
toDateString()
toISOString()
toJSON()
toLocaleDateString()
toLocaleTimeString()
toLocaleString()
toString()
toTimeString()
toUTCString()
UTC()
valueOf()

JS Error
name
message

JS Global
decodeURI()
decodeURIComponent()
encodeURI()
encodeURIComponent()
escape()
eval()
Infinity
isFinite()
isNaN()
NaN
Number()
parseFloat()
parseInt()
String()
undefined
unescape()

JS JSON
parse()
stringify()

JS Math
abs()
acos()
acosh()
asin()
asinh()
atan()
atan2()
atanh()
cbrt()
ceil()
clz32()
cos()
cosh()
E
exp()
expm1()
floor()
fround()
LN2
LN10
log()
log10()
log1p()
log2()
LOG2E
LOG10E
max()
min()
PI
pow()
random()
round()
sign()
sin()
sqrt()
SQRT1_2
SQRT2
tan()
tanh()
trunc()

JS Number
constructor
isFinite()
isInteger()
isNaN()
isSafeInteger()
MAX_VALUE
MIN_VALUE
NEGATIVE_INFINITY
NaN
POSITIVE_INFINITY
prototype
toExponential()
toFixed()
toLocaleString()
toPrecision()
toString()
valueOf()

JS OperatorsJS RegExp
constructor
compile()
exec()
g
global
i
ignoreCase
lastIndex
m
multiline
n+
n*
n?
n{X}
n{X,Y}
n{X,}
n$
^n
?=n
?!n
source
test()
toString()

(x|y)
.
\w
\W
\d
\D
\s
\S
\b
\B
\0
\n
\f
\r
\t
\v
\xxx
\xdd
\uxxxx

JS Statements
break
class
continue
debugger
do…while
for
for…in
for…of
function
if…else
return
switch
throw
try…catch
var
while

JS String
charAt()
charCodeAt()
concat()
constructor
endsWith()
fromCharCode()
includes()
indexOf()
lastIndexOf()
length
localeCompare()
match()
prototype
repeat()
replace()
search()
slice()
split()
startsWith()
substr()
substring()
toLocaleLowerCase()
toLocaleUpperCase()
toLowerCase()
toString()
toUpperCase()
trim()
valueOf()

Примечания

1. ↑
2.  (недоступная ссылка). Дата обращения: 8 августа 2015.
3. Кнут Д. Э. Искусство программирования. Том 1. Основные алгоритмы = The Art of Computer Programming. Volume 1. Fundamental Algorithms / под ред. С. Г. Тригуб (гл. 1), Ю. Г. Гордиенко (гл. 2) и И. В. Красикова (разд. 2.5 и 2.6). — 3. — Москва: Вильямс, 2002. — Т. 1. — 720 с. — ISBN 5-8459-0080-8.
4. A’Hearn, B., J. Baten, D. Crayen (2009). «Quantifying Quantitative Literacy: Age Heaping and the History of Human Capital», Journal of Economic History 69, 783—808.
5. ↑ . www.metrologie.ru. Дата обращения: 10 августа 2019.
6. . StudFiles. Дата обращения: 10 августа 2019.
7. . sv777.ru. Дата обращения: 8 августа 2019.
8. В. М. Заварыкин, В. Г. Житомирский, М. П. Лапчик. Техника вычислений и алгоритмизация: Вводный курс: Учебное пособие для студентов педагогических институтов по физико-математическим специальностям. — М: Просвещение, 1987. 160 с.: ил.
9. цит. по В. Гильде, З. Альтрихтер. «С микрокалькулятором в руках». Издание второе. Перевод с немецкого Ю. А. Данилова. М:Мир, 1987, стр. 64.

Выбор способа округления

Существует несколько способов округления в зависимости от способа применения результата: округление к меньшему/ большему, округление к меньшему/ большему по модулю, округление к ближайшему целому, округление к ближайшему чётному и т. д… Округление к ближайшему целому, в свою очередь, можно делать по-разному в зависимости от того, какой результат должен получиться, если дробная часть равна 0,5. Я буду рассматривать округление к ближайшему целому, причём 0,5 будет округляться в большую (по модулю) сторону.

Требования к корректной реализации Round() заключаются в следующем:

• правильно округляет до ближайшего целого все конечные числа;
• поддерживает специальные значения (NaN, Inf, -0), возвращая их без изменений.

Я буду использовать следующие тестовые примеры для проверки корректности, в каждой паре содержатся исходное значение и предполагаемый результат выполнения функции Round():

В этом списке есть обычные числа, специальные значения и некоторые граничные случаи, с которыми простым алгоритмам сложно справиться

Обратите внимание, что, поскольку мы используем float, мы не можем использовать число 0,49999999999999999 в качестве ближайшего к 0,5, так как из-за ограниченной точности float это число в точности равно 0,5. Вместо этого я использую 0,49999999999999994

Реализации, предложенные в закрытом тикете, явно не были проверены на подобных данных, часто не работали даже те из них, которые были предложены известными людьми. Это лишний раз доказывает, насколько сложно написать Round().

int(f + 0.5)

Первая реализация, предложенная rsc, выглядела следующим образом:

Она некорректно работает с особыми значениями, отрицательными числами, числами больше math.MaxInt64 и числами, близкими к 0,5:

Floor() or Ceil()

Второй предложенный вариант учитывал отрицательные числа:

однако продолжал некорректно работать в некоторых случаях:

Первые два теста не проходят, потому что результат разности n — 0,5 равен в точности -1,0, тогда как мы ожидаем получить что-то точно большее, чем -1,0. Если посмотреть на , можно понять, как решить эту проблему.

Самое интересное, что эта ошибка не является такой уж редкой. До версии 6 точно такая же присутствовала в Java. Хорошо, что с тех пор реализация улучшилась.

int и Copysign

В третьем предложении от minux была предпринята другая попытка решить проблему отрицательных чисел:

И этот вариант всё равно ломает тесты:

Как видно, часть тестов стала проходить, однако другие начали падать. Была предпринята попытка улучшить этот алгоритм:

Однако и она провалилась:

Этот вариант выглядит лучше остальных, но и он некорректно обрабатывает особые значения и большие числа. Первую проблему можно решить с помощью дополнительных условий, но со второй справиться не так просто.

Мы рассмотрели уже четыре варианта, и в каждом из них нашлись изъяны. Настало время посмотреть, как Round() реализуют авторы различных пакетов.

Kubernetes

Kubernetes 1.7 содержит реализацию:

Она ломает следующие тесты:

Судя по тому, что функция возвращает int32, она не предназначена для работы с большими числами. Однако она некорректно работает и с числами, которые близки к 0,5.

Другие математические функции

Math.random() возвращает
псевдослучайное число в диапазоне (0; 1], например:

for(let i = ;i < 10;++i)
   console.log( Math.random() );

Причем, при
каждом запуске будем получать разные последовательности чисел.

Math.max(a, b, c…) / Math.min(a, b, c…) возвращают наибольшее/наименьшее число из переданных аргументов:

let max = Math.max(1, 2, , -10, 5, 7);
let min = Math.min(1, 2, -10, 5);
console.log( max );        // 7
console.log( min );        // -10

Число аргументов
может быть любым.

Math.pow(n, power) возвращает число n, возведённое в степень power:

console.log( Math.pow(2, 10) ); // 2 в степени 10 = 1024

Объект Math содержит
множество других функций (cos, sin) и констант,
например, PI, которыми удобно
оперировать в JavaScript.

Видео по теме

JavaScipt #1: что это такое, с чего начать, как внедрять и запускать

JavaScipt #2: способы объявления переменных и констант в стандарте ES6+

JavaScript #3: примитивные типы number, string, Infinity, NaN, boolean, null, undefined, Symbol

JavaScript #4: приведение типов, оператор присваивания, функции alert, prompt, confirm

JavaScript #5: арифметические операции: +, -, *, /, **, %, ++, —

JavaScript #6: условные операторы if и switch, сравнение строк, строгое сравнение

JavaScript #7: операторы циклов for, while, do while, операторы break и continue

JavaScript #8: объявление функций по Function Declaration, аргументы по умолчанию

JavaScript #9: функции по Function Expression, анонимные функции, callback-функции

JavaScript #10: анонимные и стрелочные функции, функциональное выражение

JavaScript #11: объекты, цикл for in

JavaScript #12: методы объектов, ключевое слово this

JavaScript #13: клонирование объектов, функции конструкторы

JavaScript #14: массивы (array), методы push, pop, shift, unshift, многомерные массивы

JavaScript #15: методы массивов: splice, slice, indexOf, find, filter, forEach, sort, split, join

JavaScript #16: числовые методы toString, floor, ceil, round, random, parseInt и другие

JavaScript #17: методы строк — length, toLowerCase, indexOf, includes, startsWith, slice, substring

JavaScript #18: коллекции Map и Set

JavaScript #19: деструктурирующее присваивание

JavaScript #20: рекурсивные функции, остаточные аргументы, оператор расширения

JavaScript #21: замыкания, лексическое окружение, вложенные функции

JavaScript #22: свойства name, length и методы call, apply, bind функций

JavaScript #23: создание функций (new Function), функции setTimeout, setInterval и clearInterval

Как округлить до целого числа в Excel?

Чтобы округлить до целого в большую сторону используем функцию «ОКРУГЛВВЕРХ». Чтобы округлить до целого в меньшую сторону используем функцию «ОКРУГЛВНИЗ». Функция «ОКРУГЛ» и формата ячеек так же позволяют округлить до целого числа, установив количество разрядов – «0» (см.выше).

В программе Excel для округления до целого числа применяется также функция «ОТБР». Она просто отбрасывает знаки после запятой. По сути, округления не происходит. Формула отсекает цифры до назначенного разряда.

Сравните:

Второй аргумент «0» – функция отсекает до целого числа; «1» – до десятой доли; «2» – до сотой доли и т.д.

Специальная функция Excel, которая вернет только целое число, – «ЦЕЛОЕ». Имеет единственный аргумент – «Число». Можно указать числовое значение либо ссылку на ячейку.

Недостаток использования функции «ЦЕЛОЕ» – округляет только в меньшую сторону.

Округлить до целого в Excel можно с помощью функций «ОКРВВЕРХ» и «ОКРВНИЗ». Округление происходит в большую или меньшую сторону до ближайшего целого числа.

Пример использования функций:

Второй аргумент – указание на разряд, до которого должно произойти округление (10 – до десятков, 100 – до сотен и т.д.).

Округление до ближайшего целого четного выполняет функция «ЧЕТН», до ближайшего нечетного – «НЕЧЕТ».

Пример их использования:

Округление с помощью кнопок на ленте

Самый простой способ изменить округление — это выделить ячейку или группу ячеек и, находясь на вкладке «Главная», нажать на ленте на кнопку «Увеличить разрядность» или «Уменьшить разрядность». Обе кнопки располагаются в блоке инструментов «Число». Будет округляться только отображаемое число, но для вычислений при необходимости будут задействованы до 15 разрядов чисел.

При нажатии на кнопку «Увеличить разрядность» количество внесенных знаков после запятой увеличивается на один.

Кнопка «Уменьшить разрядность», соответственно, уменьшает на одну количество цифр после запятой.

Установка точности расчетов

Если в предыдущих случаях устанавливаемые параметры влияли только на внешнее отображения данных, а при расчетах использовались более точные показатели (до 15 знака), то сейчас мы расскажем, как изменить саму точность расчетов.

1. Перейдите на вкладку «Файл», оттуда — в раздел «Параметры».

Откроется окно параметров Excel. В этом окне зайдите в подраздел «Дополнительно». Отыщите блок настроек под названием «При пересчете этой книги». Настройки в этом блоке применяются не к одному листу, а к книге в целом, то есть ко всему файлу. Поставьте галочку напротив параметра «Задать точность как на экране» и нажмите «OK».

Теперь при расчете данных будет учитываться отображаемая величина числа на экране, а не та, которая хранится в памяти Excel. Настройку же отображаемого числа можно провести любым из двух способов, о которых мы говорили выше.

Интересный факт о strictfp

В Java есть специальное ключевое слово (strict floating point), которого нет в других языках программирования. И знаете, зачем оно нужно? Оно ухудшает точность работы с вещественными числами. История его появления примерно такова:

Создатели Java:

Мы очень хотим, чтобы Java была суперпопулярна, и программы на Java выполнялись на как можно большем количестве устройств. Поэтому мы прописали в спецификацию Java-машины, что на всех типах устройств все программы должны выполняться одинаково!

Создатели процессора Intel:

Ребята, мы улучшили наши процессоры, и теперь все вещественные числа внутри процессора будет представлены не 8-ю, а 10-ю байтами. Больше байт — больше знаковых цифр. А это значит что? Правильно: теперь ваши научные вычисления будут еще более точными!

Ученые и все, кто занимается сверхточными расчетами:

Круто! Молодцы. Отличная новость.

Создатели Java:

Не-не-не, ребята. Мы же сказали: все Java-программы должны выполняться одинаково на всех устройствах. Принудительно выключаем возможность использования 10 байтовых вещественных чисел внутри процессоров Intel.

Вот теперь все опять отлично! Не благодарите.

Ученые и все, кто занимается сверхточными расчетами:

Да вы там совсем охренели? Ану быстро вернули все как было!

Создатели Java:

Ребята, это для вашей же пользы! Только представьте: все Java-программы выполняются одинаково на всех устройствах. Ну круто же!

Ученые и все, кто занимается сверхточными расчетами:

Нет. Совсем не круто. Быстро вернули все обратно! Или мы вашу Java вам знаете куда засунем?

Создатели Java:

Гм. Что же вы сразу не сказали. Конечно, вернем.

Вернули возможность пользоваться всеми фичами крутых процессоров.

Кстати. Мы так же специально добавили в язык слово : если его написать перед именем функции, вся работа с вещественными числами внутри этой функции будет одинаково плохой на всех устройствах!

Примечания

1. ↑
2. Кнут Д. Э. Искусство программирования. Том 1. Основные алгоритмы = The Art of Computer Programming. Volume 1. Fundamental Algorithms / под ред. С. Г. Тригуб (гл. 1), Ю. Г. Гордиенко (гл. 2) и И. В. Красикова (разд. 2.5 и 2.6). — 3. — Москва: Вильямс, 2002. — Т. 1. — 720 с. — ISBN 5-8459-0080-8.
3. A’HEARN, B., J. BATEN AND D. CRAYEN (2009). “Quantifying Quantitative Literacy: Age Heaping and the History of Human Capital”, Journal of Economic History 69,783-808.
4. В. М. Заварыкин, В. Г. Житомирский, М. П. Лапчик. Техника вычислений и алгоритмизация: Вводный курс: Учебное пособие для студентов педагогических институтов по физико-математическим специальностям. — М: Просвещение, 1987. 160 с.: ил.
5. цит. по В. Гильде, З. Альтрихтер. «С микрокалькулятором в руках». Издание второе. Перевод с немецкого Ю. А. Данилова. М:Мир, 1987, стр. 64.

Обозначения

Операция округления числа x к большему (вверх) обозначается следующим образом: ⌈x⌉{\displaystyle \lceil x\rceil }. Аналогично, округление к меньшему (вниз) обозначается ⌊x⌋{\displaystyle \lfloor x\rfloor }. Эти символы (а также английские названия для этих операций — соответственно, ceiling и floor, досл. «потолок» и «пол») были введеныК. Айверсоном в его работе A Programming Language, описавшей систему математических обозначений, позже развившуюся в язык программирования APL. Айверсоновские обозначения операций округления были популяризированы Д. Кнутом в его книге «Искусство программирования».

По аналогии, округление к ближайшему целому часто обозначают как x{\displaystyle \left}. В некоторых прежних и современных (вплоть до конца XX века) работах так обозначалось округление к меньшему; такое использование этого обозначения восходит ещё к работе Гаусса 1808 года (третье его доказательство квадратичного закона взаимности). Кроме того, это же обозначение используется (с другим значением) в нотации Айверсона.

В стандарте Юникод зафиксированы следующие символы:

Названиев Юникоде	Код в Юникоде	Вид	Мнемоникав HTML 4	Примечания
16-ричный	десятичный
LEFT CEILING (тж. APL upstile)	2308	8968	⌈	⌈	не путать с: U+2E22 ⸢ — Top left half bracket U+300C 「 — Left corner bracket
RIGHT CEILING	2309	8969	⌉	⌉	не путать с: U+20E7 ◌⃧ — Combining annuity symbol U+2E23 ⸣ — Top right half bracket
LEFT FLOOR (тж. APL downstile)	230A	8970	⌊	⌊	не путать с:
RIGHT FLOOR	230B	8971	⌋	⌋	не путать с: U+2E25 ⸥ — Bottom right half bracket U+300D 」 — Right corner bracket

Изменение количества отображаемых знаков после запятой без изменения числового значения

Выполнение такого рода действия осуществляется при помощи настроек числового формата, путем уменьшения количества знаков после запятой, при этом само числовое значение не округляется, округляется только его отображение на экране монитора. Внести изменения в настройки числового формата, можно при помощи кнопок «Увеличить разрядность» и «Уменьшить разрядность» на ленте Excel 2007 во вкладке «Главная», в группе «Число».

В других версиях Excel эти кнопки выглядят аналогично. Изменения в настройки числового формата, а именно увеличение либо уменьшение количества отображаемых знаков после запятой, можно внести в настройках формата ячеек. Не буду повторять о том, как вызвать окно “Формат ячеек” разными способами, так как ранее этот вопрос уже рассматривался. Использование вышеописанного метода округления может приводить к некоторым нежелательным последствиям, например вот к такому:

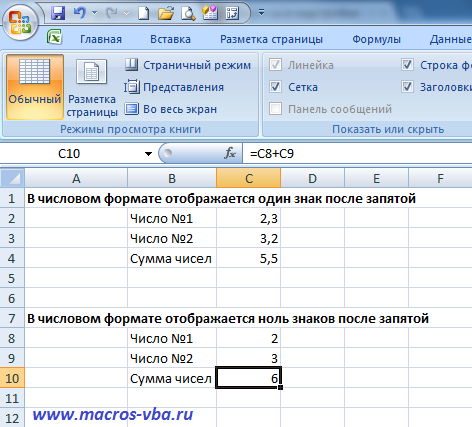
Как видно из примера, некорректная настройка числового формата привела к тому, что 2+3=6, что неверно.

Варианты округления 0,5 к ближайшему целому

Отдельного описания требуют правила округления для специального случая, когда (N+1)-й знак = 5, а последующие знаки равны нулю. Если во всех остальных случаях округление до ближайшего целого обеспечивает меньшую погрешность округления, то данный частный случай характерен тем, что для однократного округления формально безразлично, производить его «вверх» или «вниз» — в обоих случаях вносится погрешность ровно в 1/2 младшего разряда. Существуют следующие варианты правила округления до ближайшего целого для данного случая:

• Математическое округление — округление всегда в бо́льшую по модулю сторону (предыдущий разряд всегда увеличивается на единицу).
• Банковское округление (англ. banker’s rounding) — округление для этого случая происходит к ближайшему чётному, то есть 2,5 → 2; 3,5 → 4.
• Случайное округление — округление происходит в меньшую или большую сторону в случайном порядке, но с равной вероятностью (может использоваться в статистике). Также часто используется округление с неравными вероятностями (вероятность округления вверх равна дробной части), этот способ делает накопление ошибок случайной величиной с нулевым математическим ожиданием.
• Чередующееся округление — округление происходит в меньшую или большую сторону поочерёдно.

Во всех вариантах в случае, когда (N+1)-й знак не равен 5 или последующие знаки не равны нулю, округление происходит по обычным правилам: 2,49 → 2; 2,51 → 3.

Математическое округление просто формально соответствует общему правилу округления (см. выше). Его недостатком является то, что при округлении большого числа значений, которые далее будут обрабатываться совместно, может происходить накопление ошибки округления. Типичный пример: округление до целых рублей денежных сумм, выражаемых в рублях и копейках. В реестре из 10 000 строк (если считать копеечную часть каждой суммы случайным числом с равномерным распределением, что обычно вполне допустимо) окажется в среднем около 100 строк с суммами, содержащими в части копеек значение 50. При округлении всех таких строк по правилам математического округления «вверх» сумма «итого» по округлённому реестру окажется на 50 рублей больше точной.

Три остальных варианта как раз и придуманы для того, чтобы уменьшить общую погрешность суммы при округлении большого количества значений. Округление «до ближайшего чётного» исходит из предположения, что при большом числе округляемых значений, имеющих 0,5 в округляемом остатке, в среднем половина из них окажется слева, а половина — справа от ближайшего чётного, таким образом, ошибки округления взаимно погасятся. Строго говоря, предположение это верно лишь тогда, когда набор округляемых чисел обладает свойствами случайного ряда, что обычно верно в бухгалтерских приложениях, где речь идёт о ценах, суммах на счетах и так далее. Если же предположение будет нарушено, то и округление «до чётного» может приводить к систематическим ошибкам. Для таких случаев лучше работают два следующих метода.

Два последних варианта округления гарантируют, что примерно половина специальных значений будет округлена в одну сторону, половина — в другую. Но реализация таких методов на практике требует дополнительных усилий по организации вычислительного процесса.

• Округление в случайную сторону требует для каждой округляемой строки генерировать случайное число. При использовании псевдослучайных чисел, создаваемых линейным реккурентным методом, для генерации каждого числа требуется операция умножения, сложения и деления по модулю, что для больших объёмов данных может существенно замедлить расчёты.
• Чередующееся округление требует хранить флаг, показывающий, в какую сторону последний раз округлялось специальное значение, и при каждой операции переключать значение этого флага.