№32 функция round() / для начинающих
Содержание:
- Важные заметки о числах
- Шестнадцатеричные, двоичные и восьмеричные числа в JavaScript
- Округление числа
- Случайное число
- Неточные вычисления
- Сравнение чисел
- Великий и могучий Math
- Остальные математические методы
- Как явно преобразовать строку в число
- Сравнение дробных чисел
- Комментарии
- Floor(Double)
- Выбор способа округления
- Relational functions #
- Как проверить является ли переменная числом
- Matrix functions #
- АргументыArguments
- Итого
Важные заметки о числах
Для начала запомните, что в js все виды чисел (дробные и целые) относятся к типу Number
. К тому же все они 64-битные, так как хранятся в формате «double precision», который также известен под стандартом IEEE-754.
Создаются численные переменные привычным способом:
Поддерживает и другие числовые представления. Так, еще можно создавать числа с плавающей точкой (их еще иногда называют «числа в научном формате»).
В появилась поддержка очень интересного метода toLocaleString ()
, который форматирует все числовые параметры по спецификациям, прописанным в ECMA 402. Благодаря этому большие числа, телефонные номера, валюты и даже проценты красиво выводятся в диалоговом окне.
Для работы с элементами типа Number был предусмотрен целый глобальный объект с кучей всевозможных математических функций, имя которого Math
.
Помимо этого, существуют и другие методы, которые выполняют округление числовых значений до целых чисел, до десятых, сотых и т.д. Рассмотрим их все подробнее.
Шестнадцатеричные, двоичные и восьмеричные числа в JavaScript
Шестнадцатеричные числа широко используются в JavaScript для представления цветов, кодировки символов и многого другого.
Короткий стиль записи шестнадцатеричного числа:
0x, после которого указывается число.
Например:
JavaScript
alert( 0xff ); // 255
alert( 0xFF ); // 255 (тоже самое, регистр не имеет значения)
|
1 |
alert(0xff);// 255 alert(0xFF);// 255 (тоже самое, регистр не имеет значения) |
Замечание по двоичным и восьмеричным числам
Не так часто используются двоичные и восьмеричные числа, но они также поддерживаются 0b для двоичных и 0o для восьмеричных.
Короткий стиль записи двоичного числа:
JavaScript
let a = 0b11111111; // бинарная форма записи числа 255
| 1 | leta=0b11111111;// бинарная форма записи числа 255 |
Короткий стиль записи восьмеричного числа:
JavaScript
let b = 0o377; // восьмеричная форма записи числа 255
| 1 | letb=0o377;// восьмеричная форма записи числа 255 |
Округление числа
Часто результатом расчётов бывает число с большим количеством знаков после запятой. Если это число будет
использовано для дальнейших
расчётов, то его можно оставить в таком виде. Но иногда требуется округление числа, например для вывода
на страницу.
В JavaScript округление чисел осуществляется несколькими методами.
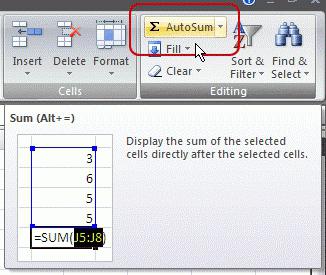
Метод Math.round() округляет значение до целого числа.
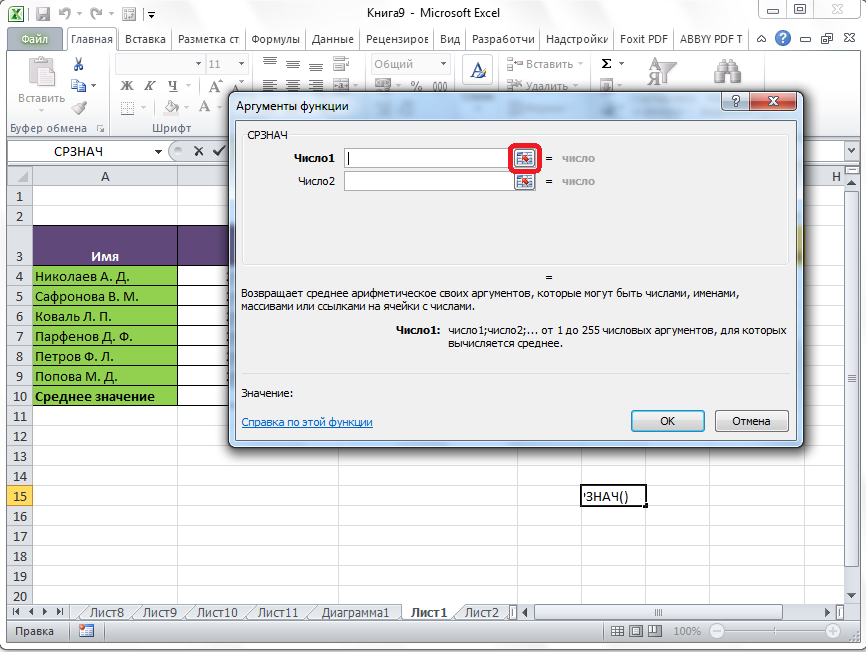
Math.round (число)
Округление числа производится по математическим
правилам. То есть, если после запятой идёт цифра от 0 до 4, то дробная часть просто отбрасывается. А если
после запятой идёт цифра от 5 до 9, то дробрая часть отбрасывается, а к целой части прибавляется единица.
пример:
+
| 910 |
var x = 5.83; console.log(Math.round(x)); //вернёт: 6 |
Метод toFixed() округляет число до заданной точности.
число.toFixed (точность)
Параметры:
точность — количество знаков после запятой, до которого округляется число
Этот метод возвращает не число а строку. Чтобы преобразовать её в число можно добавить + к возвращаемому
значению. Пример:
| 1112 |
var num = x.toFixed(1); console.log(+num); //вернёт: 5.8 |
Есть ещё два метода, которые округляют число до целого значения. Метод
Math.floor() округляет в меньшую сторону. Он отбрасывает дробную часть числа.
А метод Math.ceil() округляет в большую сторону. Он отбрасывает дробную часть,
а к целой части прибавляет единицу. Пример:
| 1314 |
console.log(Math.floor(x)); // вернёт 5 console.log(Math.ceil(x)); // вернёт 6 |
Случайное число
Метод Math.random() генерирует
псевдо-случайное число в диапазоне от 0 до 1. При
этом ровно 1 не бывает, число вегда будет меньше.
Обычно случайное число нужно получить в каком-то конкретном
диапазоне. Для этого можно использовать формулу:
случайное число = минимум + Math.random() * (максимум — минимум)
Для примера выведем число в диапазоне от -2 до 5:
| 1617 |
var rand = -2 + Math.random() * (5 - (-2)); console.log(rand); |
Конечно, 5 — (-2) это 5+2.
Не завбывайте, что число 5 Вы в этой формуле не получите. Максимальное будет
4.999999999. Полученные значения можно округлить до нужной точности.
Если нужны только целые числа, то полученные значения можно округлять до целого в меньшую сторону. К
максимуму нужно прибавить единицу, чтобы этот максимум тоже был возможен. Формула получается такая:
целое число = Math.floor (минимум + Math.random() * (максимум+1 — минимум))
Выведем числа от 10 до 15:
| 1920 |
rand = Math.floor(10 + Math.random() * (15 + 1 - 10)); console.log(rand); |
Неточные вычисления
Внутри JavaScript число представлено в виде 64-битного формата IEEE-754. Для хранения числа используется 64 бита: 52 из них используется для хранения цифр, 11 из них для хранения положения десятичной точки (если число целое, то хранится 0), и один бит отведён на хранение знака.
Если число слишком большое, оно переполнит 64-битное хранилище, JavaScript вернёт бесконечность:
Наиболее часто встречающаяся ошибка при работе с числами в JavaScript – это потеря точности.
Посмотрите на это (неверное!) сравнение:
Да-да, сумма и не равна .
Странно! Что тогда, если не ?
Но почему это происходит?
Число хранится в памяти в бинарной форме, как последовательность бит – единиц и нулей. Но дроби, такие как , , которые выглядят довольно просто в десятичной системе счисления, на самом деле являются бесконечной дробью в двоичной форме.
Другими словами, что такое ? Это единица делённая на десять — , одна десятая. В десятичной системе счисления такие числа легко представимы, по сравнению с одной третьей: , которая становится бесконечной дробью .
Деление на гарантированно хорошо работает в десятичной системе, но деление на – нет. По той же причине и в двоичной системе счисления, деление на обязательно сработает, а становится бесконечной дробью.
В JavaScript нет возможности для хранения точных значений 0.1 или 0.2, используя двоичную систему, точно также, как нет возможности хранить одну третью в десятичной системе счисления.
Числовой формат IEEE-754 решает эту проблему путём округления до ближайшего возможного числа. Правила округления обычно не позволяют нам увидеть эту «крошечную потерю точности», но она существует.
Пример:
И когда мы суммируем 2 числа, их «неточности» тоже суммируются.
Вот почему – это не совсем .
Не только в JavaScript
Справедливости ради заметим, что ошибка в точности вычислений для чисел с плавающей точкой сохраняется в любом другом языке, где используется формат IEEE 754, включая PHP, Java, C, Perl, Ruby.
Можно ли обойти проблему? Конечно, наиболее надёжный способ — это округлить результат используя метод toFixed(n):
Также можно временно умножить число на 100 (или на большее), чтобы привести его к целому, выполнить математические действия, а после разделить обратно. Суммируя целые числа, мы уменьшаем погрешность, но она все равно появляется при финальном делении:
Таким образом, метод умножения/деления уменьшает погрешность, но полностью её не решает.
Забавный пример
Попробуйте выполнить его:
Причина та же – потеря точности. Из 64 бит, отведённых на число, сами цифры числа занимают до 52 бит, остальные 11 бит хранят позицию десятичной точки и один бит – знак. Так что если 52 бит не хватает на цифры, то при записи пропадут младшие разряды.
Интерпретатор не выдаст ошибку, но в результате получится «не совсем то число», что мы и видим в примере выше. Как говорится: «как смог, так записал».
Два нуля
Другим забавным следствием внутреннего представления чисел является наличие двух нулей: и .
Все потому, что знак представлен отдельным битом, так что, любое число может быть положительным и отрицательным, включая нуль.
В большинстве случаев это поведение незаметно, так как операторы в JavaScript воспринимают их одинаковыми.
Сравнение чисел
Для сравнения чисел в JavaScript используются следующие операторы: == (равно), != (не равно), > (больше), = (больше или равно),
Например, сравним два числа:
Console.log(2>3); //false
console.log(5>=3); //true
При сравнении чисел с дробной частью необходимо учитывать погрешности, которые могут возникать во время этих вычислений.
Например, в JavaScript сумма чисел (0.2 + 0.4) не равна 0.6:
Console.log((0.2+0.4)==0.6); //false
Погрешности происходят потому что все вычисления компьютер или другое электронное устройство производит в 2 системе счисления. Т.е. перед тем как выполнить какие-то действия компьютер сначала должен преобразовать представленные в выражении числа в 2 систему счисления. Но, не любое дробное десятичное число можно представить в 2 системе счисления точно.
Например, число 0.25 10 в двоичную систему преобразуется точно.
0.125 × 2 = 0.25 | 0
0.25 × 2 = 0.5 | 0
0.5 × 2 = 1 | 1
0.125 10 = 0.001 2
Например, число 0.2 10 можно преобразовать в 2 систему только с определённой точностью:
0.2 × 2 = 0.4 | 0
0.4 × 2 = 0.8 | 0
0.8 × 2 = 1.6 | 1
0.6 × 2 = 1.2 | 1
0.2 × 2 = 0.4 | 0
0.4 × 2 = 0.8 | 0
0.8 × 2 = 1.6 | 1
0.6 × 2 = 1.2 | 1
0.2 × 2 = 0.4 | 0
0.4 × 2 = 0.8 | 0
0.8 × 2 = 1.6 | 1
0.6 × 2 = 1.2 | 1
…
0.2 10 = 0.001100110011… 2
В результате эти погрешности скажутся при вычисления суммы двух чисел и результатах сравнения. Т.е. получится что на самом деле JavaScript будет видет эту запись следующим образом:
0.6000000000000001==0.6
При вычислениях или отображении чисел с дробной частью необходимо всегда указывать точность, с которой это необходимо делать.
Например, сравнить числа до 2 знаков после запятой используя методы toFixed() и toPrecision() :
//метод toFixed()
console.log((0.2+0.4).toFixed(2)==(0.6).toFixed(2)); //true
//метод toPrecision()
console.log((0.2+0.4).toPrecision(2)==(0.6).toPrecision(2)); //true
Основные математические операции
В JavaScript существуют следующие математические операторы: + (сложение), — (вычитание), * (умножение), / (деление), % (остаток от деления), ++ (увелить значение на 1), — (уменьшить значение на 1).
6+3 //9
6-3 //3
6*3 //18
6/3 //2
6%3 //0, т.е. 6:3=2 => 6-3*2 => ост(0)
5%2 //1, т.е. 5:2=2(.5) => 5-2*2 => ост(1)
7.3%2 //1.3, т.е. 7.3:2=3(.65) => 7.3-2*3 => ост(1.3)
//знак результата операции % равен знаку первого значения
-9%2.5 //-1.5, т.е. 9:2.5=3(.6) => 9-2.5*3 => ост(1.5)
-9%-2.5 //-1.5, т.е. 9:2.5=3(.6) => 9-2.5*3 => ост(1.5)
-2%5 //-2, т.е. 2:5=0(.4) => 2-5*0 => ост(2)
x = 3;
console.log(x++); //выводит 3, у уже потом устанавливает 4
console.log(x); //4
x = 3;
console.log(++x); //устанавливает 4 и выводит
x = 5;
console.log(x—); //выводит 5, у уже потом устанавливает 4
console.log(x); //4
x = 5;
console.log(—x); //устанавливает 4 и выводит
Кроме этого в JavaScript есть комбинированные операторы: x+=y (x=x+y), x-=y (x=x-y), x*=y (x=x*y), x/=y (x=x/y), x%=y (x=x%y).
x = 3;
y = 6;
x+=y;
console.log(x); //9
x = 3;
y = 6;
x-=y;
console.log(x); //-3
x = 3;
y = 6;
x*=y;
console.log(x); //18
x = 3;
y = 6;
x/=y;
console.log(x); //0.5
x = 3;
y = 6;
x%=y;
console.log(x); //3
Здравствуйте, любители JavaScript-а. Вы уже заметили, что этот язык очень неординарен и в каждом разделе выделяется своими особенностями и необычными техническими решениями. Поэтому сегодняшняя публикация посвящается теме: «JavaScript округление».
После прочтения текущей статьи вы узнаете, для чего необходимо округлять числа, какие методы и свойства в js выполняют эту функцию, а также чем выделяется деление на 0. Не изменяя своим принципам, я прикреплю примеры к ключевым моментам материала и подробно распишу каждое действие. А теперь давайте приступать к обучению!
Великий и могучий Math
Глобальный объект Math включает в себя огромное количество разнообразных математических и тригонометрических функций. Это очень нужный объект и часто выручает разработчиков при работе с цифровыми данными.
На других платформах существуют аналогии Math. Например, в таких популярных языках, как Java и C#, Math представляет собой класс, который поддерживает все те же стандартные функции. Так что как видите этот инструмент действительно великий и могучий.
Теперь я хочу пройтись по конкретным методам, отвечающим за округление, и подробно о них рассказать.
Math.floor ()
Начну с Math.
floor
Обратите внимание на наименование метода. Логически становится понятно, что раз речь идет об округлении, а дословный перевод слова «floor» означает «пол», то данный инструмент округлит обрабатываемые значения в меньшую строну
Также возможен вариант, когда обработанное число с помощью этой функции осталось прежним. Все потому, что округление осуществляется по нестрогому неравенству (
в ответе будет число 4.
Math.ceil ()
Опять-таки посмотрите на название (в такой способ материал быстрее усваивается). Если кто-то не знает, то «ceil» означает «потолок». Значит округление числовых данных будет осуществляться в большую сторону, используя нестрогое неравенство (>=).
Как вы уже догадались, в ответе будет число 5.
Math.round ()
Данный метод округляет дробное число до ближайшего целого. Так, если дробная часть находится в диапазоне от 0 и до 0.5 не включительно, то округление происходит к меньшему значению. А если дробная часть находится в диапазоне от включительно 0.5 и до следующего целого числа, то она округляется к большему целому.
Надеюсь, все подумали или сказали правильный ответ – 5.
Остальные математические методы
Есть достаточно много методов для различных математических вычислений. Они простые и не требуют
дополнительных разъяснений. Методы, которые часто используются, перечислены в следующей таблице:
| Метод | Значение |
| Math.pow(x, y) | Возводит x в степень y |
| Math.exp(x) | Экспонента числа x |
| Math.sqrt(x) | Квадратный корень из числа x |
| Math.log(x) | Натуральный логорифм числа x |
| Math.abs(x) | Модуль числа x |
| Math.max(a, b, c) | Максимальное из чисел |
| Math.min(a, b, c) | Минимальное из чисел |
| Math.sin(x) | Синус числа x |
| Math.cos(x) | Косинус числа x |
| Math.tan(x) | Тангенс числа x |
Попробуйте произвести какие-нибудь вычисления с использованием этих методов.
Как явно преобразовать строку в число
Явно привести строку в число можно посредством следующих способов:
1. Использовать унарный оператор +, который необходимо поместить перед значением.
+'7.35'; // 7.35 +'текст'; // NaN
Этот способ пренебрегает пробелами в начале и конце строки, а также (переводом строки).
+' 7.35 '; //7.35 +'7.35 \n '; //7.35
Используя данный способ необходимо обратить внимание на то, что пустая строка или строка, состоящая из пробелов и , переводится в число 0. Кроме этого она также преобразует тип данных и логические значения к числу
+null; //0 +true; //1 +false; //0 +' '; //0
2. Функция parseInt. Данная функция предназначена для преобразования аргумента в целое число. В отличие от использования унарного оператора +, данный метод позволяет преобразовать строку в число, в которой не все символы являются цифровыми. Начинает она преобразовывать строку, начиная с первого символа. И как только она встречает символ, не являющийся цифровым, данная функция останавливает свою работу и возвращает полученное число.
parseInt('18px'); //18
parseInt('33.3%'); //33
Данная функция может работать с разными системами счисления (двоичной, восьмеричной, десятичной, шестнадцатеричной). Указание основание системы счисления осуществляется посредством 2 аргумента.
Кроме этого рекомендуется, всегда указывать основание системы счисления и не полагаться на значение по умолчанию установленное этой функции, например в том или ином браузере.
parseInt('18px', 10); //18
parseInt('33.3%', 10); //33
parseInt('101',2); //5
parseInt('B5',16); //181
Кроме функции parseInt в JavaScript имеется метод Number.parseInt. Данный метод ничем не отличается от функции parseInt и был введён в JavaScript со спецификацией ECMASCRIPT 2015 (6).
3. Функция parseFloat. Функция parseFloat аналогична parseInt, за исключением того что позволяет выполнить преобразование аргумента в дробное число.
parseFloat('33.3%'); //33.3
Кроме этого функция parseFloat в отличие от parseInt не имеет 2 аргумента, и следовательно она всегда пытается рассмотреть строку как число в десятичной системе счисления.
parseFloat("3.14");
parseFloat("314e-2");
parseFloat("0.0314E+2");
Кроме функции parseFloat в JavaScript имеется метод Number.parseFloat. Данный метод ничем не отличается от функции parseFloat и был введён в JavaScript со спецификацией ECMASCRIPT 2015 (6).
Сравнение дробных чисел
У математических вычислений есть одна особенность — их результат не всегда абсолютно точный. Это проблема
не только JavaScript, но и большинства языков программирования. Так происходит потому, что числа и другие
данные переводятся в двоичный код, и только потом с ними производятся вычисления. В большинстве случаев это
не приводит к особенным трудностям, просто в результате расчётов иногда получается число с большим количеством
знаков после запятой. Но есть ситуация, когда неточность вычислений влияет на работу программы. Это сравнение
чисел. Если сравниваются разные числа, то здесь всё должно быть нормально.
5.1
Но если при вычислении получаются два одинаковых дробных числа, то результат их сравнения не предсказуем.
Они могут быть равны, либо одно может быть больше другого. Когда в скрипте
используется такое сравнение,
то нужно проверять, правильно ли работает скрипт. Если в нём есть ошибка, то нужно округлять значения, которые
сравниваются.
Комментарии
Поведение этого метода соответствует стандарту IEEE 754, разделу 4.The behavior of this method follows IEEE Standard 754, section 4. Этот тип округления иногда называют округлением в сторону отрицательной бесконечности.This kind of rounding is sometimes called rounding toward negative infinity.
Floor(Double)
Возвращает наибольшее целое число, которое меньше или равно заданному числу с плавающей запятой двойной точности.Returns the largest integral value less than or equal to the specified double-precision floating-point number.
-
d
- Double
Число двойной точности с плавающей запятой.A double-precision floating-point number.
Возвращаемое значение
- Double
Наибольшее целое число, которое меньше или равно .The largest integral value less than or equal to . Если значение параметра равно NaN, NegativeInfinity или PositiveInfinity, возвращается это значение.If is equal to NaN, NegativeInfinity, or PositiveInfinity, that value is returned.
Примеры
В следующем примере показан метод и его отличие от метода.The following example illustrates the method and contrasts it with the method.
Комментарии
Поведение этого метода соответствует стандарту IEEE 754, разделу 4.The behavior of this method follows IEEE Standard 754, section 4. Этот тип округления иногда называют округлением в сторону отрицательной бесконечности.This kind of rounding is sometimes called rounding toward negative infinity. Иными словами, если является положительным, любой дробный компонент усекается.In other words, if is positive, any fractional component is truncated. Если имеет отрицательное значение, присутствие любого компонента дробной части приводит к округлению его до меньшего целого числа.If is negative, the presence of any fractional component causes it to be rounded to the smaller integer. Операция этого метода отличается от Ceiling метода, который поддерживает округление в сторону положительной бесконечности.The operation of this method differs from the Ceiling method, which supports rounding toward positive infinity.
Начиная с Visual Basic 15,8, производительность преобразования типа «двойное в целое число» оптимизирована, если передать значение, возвращаемое методом, в любую функцию целочисленного преобразованияили если значение Double, возвращаемое, автоматически преобразуется в целое число с параметром Option-on , равным OFF.Starting with Visual Basic 15.8, the performance of Double-to-integer conversion is optimized if you pass the value returned by the method to the any of the integral conversion functions, or if the Double value returned by is automatically converted to an integer with Option Strict set to Off. Эта оптимизация позволяет коду выполняться быстрее — до двух раз быстрее для кода, который выполняет большое количество преобразований в целочисленные типы.This optimization allows code to run faster — up to twice as fast for code that does a large number of conversions to integer types. В следующем примере показаны оптимизированные преобразования:The following example illustrates such optimized conversions:
Выбор способа округления
Существует несколько способов округления в зависимости от способа применения результата: округление к меньшему/ большему, округление к меньшему/ большему по модулю, округление к ближайшему целому, округление к ближайшему чётному и т. д… Округление к ближайшему целому, в свою очередь, можно делать по-разному в зависимости от того, какой результат должен получиться, если дробная часть равна 0,5. Я буду рассматривать округление к ближайшему целому, причём 0,5 будет округляться в большую (по модулю) сторону.
Требования к корректной реализации Round() заключаются в следующем:
- правильно округляет до ближайшего целого все конечные числа;
- поддерживает специальные значения (NaN, Inf, -0), возвращая их без изменений.
Я буду использовать следующие тестовые примеры для проверки корректности, в каждой паре содержатся исходное значение и предполагаемый результат выполнения функции Round():
В этом списке есть обычные числа, специальные значения и некоторые граничные случаи, с которыми простым алгоритмам сложно справиться
Обратите внимание, что, поскольку мы используем float, мы не можем использовать число 0,49999999999999999 в качестве ближайшего к 0,5, так как из-за ограниченной точности float это число в точности равно 0,5. Вместо этого я использую 0,49999999999999994
Реализации, предложенные в закрытом тикете, явно не были проверены на подобных данных, часто не работали даже те из них, которые были предложены известными людьми. Это лишний раз доказывает, насколько сложно написать Round().
int(f + 0.5)
Первая реализация, предложенная rsc, выглядела следующим образом:
Она некорректно работает с особыми значениями, отрицательными числами, числами больше math.MaxInt64 и числами, близкими к 0,5:
Floor() or Ceil()
Второй предложенный вариант учитывал отрицательные числа:
однако продолжал некорректно работать в некоторых случаях:
Первые два теста не проходят, потому что результат разности n — 0,5 равен в точности -1,0, тогда как мы ожидаем получить что-то точно большее, чем -1,0. Если посмотреть на , можно понять, как решить эту проблему.
Самое интересное, что эта ошибка не является такой уж редкой. До версии 6 точно такая же присутствовала в Java. Хорошо, что с тех пор реализация улучшилась.
int и Copysign
В третьем предложении от minux была предпринята другая попытка решить проблему отрицательных чисел:
И этот вариант всё равно ломает тесты:
Как видно, часть тестов стала проходить, однако другие начали падать. Была предпринята попытка улучшить этот алгоритм:
Однако и она провалилась:
Этот вариант выглядит лучше остальных, но и он некорректно обрабатывает особые значения и большие числа. Первую проблему можно решить с помощью дополнительных условий, но со второй справиться не так просто.
Мы рассмотрели уже четыре варианта, и в каждом из них нашлись изъяны. Настало время посмотреть, как Round() реализуют авторы различных пакетов.
Kubernetes
Kubernetes 1.7 содержит реализацию:
Она ломает следующие тесты:
Судя по тому, что функция возвращает int32, она не предназначена для работы с большими числами. Однако она некорректно работает и с числами, которые близки к 0,5.
Relational functions #
| Function | Description |
|---|---|
| math.compare(x, y) | Compare two values. |
| math.compareNatural(x, y) | Compare two values of any type in a deterministic, natural way. |
| math.compareText(x, y) | Compare two strings lexically. |
| math.deepEqual(x, y) | Test element wise whether two matrices are equal. |
| math.equal(x, y) | Test whether two values are equal. |
| math.equalText(x, y) | Check equality of two strings. |
| math.larger(x, y) | Test whether value x is larger than y. |
| math.largerEq(x, y) | Test whether value x is larger or equal to y. |
| math.smaller(x, y) | Test whether value x is smaller than y. |
| math.smallerEq(x, y) | Test whether value x is smaller or equal to y. |
| math.unequal(x, y) | Test whether two values are unequal. |
Как проверить является ли переменная числом
Определить является ли значение переменной числом можно используя один из следующих способов:
1. С использованием функций isNaN и isFinite:
// myVar — переменная
if (!isNaN(parseFloat(myVar)) && isFinite(parseFloat(myVar))) {
//myVar — это число или может быть приведено к нему
};
В виде функции:
// функция
function isNumeric(value) {
return !isNaN(parseFloat(value)) && isFinite(parseFloat(value));
}
// использование
var myVar = «12px»;
console.log(isNumeric(myVar)); //true
Этот способ позволяет определить является ли указанное значение числом или может быть приведено к нему. Данный вариант не считает числом пустую строку, строку из пробелов, значение null , Infinity , -Infinity , true и false .
2. С использованием оператора typeof и функций isFinite, isNaN:
// функция которая проверяет является ли значение числом
function isNumber(value) {
return typeof value === «number» &&
isFinite(value) &&
!isNaN(value);
};
// использование функции isNumber
isNumber(18); //true
// использование функций для проверки текстовых значений
isNumber(parseFloat(«»)); //false
isNumber(parseFloat(«Infinity»)); //false
isNumber(parseFloat(«12px»)); //true
Эта функция определяет имеет ли указанное значение тип Number, а также не принадлежит ли оно к одному из специальных значений Infinity, -Infinity и NaN. Эсли это так, то данная функция возвращает значение true.
3. С помощью метода ECMAScript 6 Number.isInteger(value) . Данный метод позволяет определить, является ли указанное значение целым числом.
Number.isInteger(«20»); //false, т.к. данный метод не выполняет перевод строки в число
Number.isInteger(20); //true, т.к. данное значение является числом
Matrix functions #
| Function | Description |
|---|---|
| math.apply(A, dim, callback) | Apply a function that maps an array to a scalar along a given axis of a matrix or array. |
| math.column(value, index) | Return a column from a Matrix. |
| math.concat(a, b, c, … ) | Concatenate two or more matrices. |
| math.count(x) | Count the number of elements of a matrix, array or string. |
| math.cross(x, y) | Calculate the cross product for two vectors in three dimensional space. |
| math.ctranspose(x) | Transpose and complex conjugate a matrix. |
| math.det(x) | Calculate the determinant of a matrix. |
| math.diag(X) | Create a diagonal matrix or retrieve the diagonal of a matrix When is a vector, a matrix with vector on the diagonal will be returned. |
| math.diff(arr) | Create a new matrix or array of the difference between elements of the given array The optional dim parameter lets you specify the dimension to evaluate the difference of If no dimension parameter is passed it is assumed as dimension 0 Dimension is zero-based in javascript and one-based in the parser and can be a number or bignumber Arrays must be ‘rectangular’ meaning arrays like If something is passed as a matrix it will be returned as a matrix but other than that all matrices are converted to arrays. |
| math.dot(x, y) | Calculate the dot product of two vectors. |
| math.eigs(x) | Compute eigenvalue and eigenvector of a real symmetric matrix. |
| math.expm(x) | Compute the matrix exponential, expm(A) = e^A. |
| math.filter(x, test) | Filter the items in an array or one dimensional matrix. |
| math.flatten(x) | Flatten a multi dimensional matrix into a single dimensional matrix. |
| math.forEach(x, callback) | Iterate over all elements of a matrix/array, and executes the given callback function. |
| math.getMatrixDataType(x) | Find the data type of all elements in a matrix or array, for example ‘number’ if all items are a number and ‘Complex’ if all values are complex numbers. |
| math.identity(n) | Create a 2-dimensional identity matrix with size m x n or n x n. |
| math.inv(x) | Calculate the inverse of a square matrix. |
| math.kron(x, y) | Calculates the kronecker product of 2 matrices or vectors. |
| math.map(x, callback) | Create a new matrix or array with the results of the callback function executed on each entry of the matrix/array. |
| math.ones(m, n, p, …) | Create a matrix filled with ones. |
| math.partitionSelect(x, k) | Partition-based selection of an array or 1D matrix. |
| math.range(start, end ) | Create an array from a range. |
| math.reshape(x, sizes) | Reshape a multi dimensional array to fit the specified dimensions. |
| math.resize(x, size ) | Resize a matrix. |
| math.rotate(w, theta) | Rotate a vector of size 1×2 counter-clockwise by a given angle Rotate a vector of size 1×3 counter-clockwise by a given angle around the given axis. |
| math.rotationMatrix(theta) | Create a 2-dimensional counter-clockwise rotation matrix (2×2) for a given angle (expressed in radians). |
| math.row(value, index) | Return a row from a Matrix. |
| math.size(x) | Calculate the size of a matrix or scalar. |
| math.sort(x) | Sort the items in a matrix. |
| X = math.sqrtm(A) | Calculate the principal square root of a square matrix. |
| math.squeeze(x) | Squeeze a matrix, remove inner and outer singleton dimensions from a matrix. |
| math.subset(x, index ) | Get or set a subset of a matrix or string. |
| math.trace(x) | Calculate the trace of a matrix: the sum of the elements on the main diagonal of a square matrix. |
| math.transpose(x) | Transpose a matrix. |
| math.zeros(m, n, p, …) | Create a matrix filled with zeros. |
АргументыArguments
numeric_expressionnumeric_expressionВыражение категории точного числового или приблизительного числового типа данных, за исключением типа данных bit.Is an expression of the exact numeric or approximate numeric data type category, except for the bit data type.
lengthlengthТочность, с которой должно быть округлено значение numeric_expression.Is the precision to which numeric_expression is to be rounded. Аргумент length должен быть выражением типа tinyint, smallint или int. Если аргумент length является положительным числом, значение numeric_expression округляется до числа десятичных разрядов, указанных в аргументе length.length must be an expression of type tinyint, smallint, or int. When length is a positive number, numeric_expression is rounded to the number of decimal positions specified by length. Если аргумент length является отрицательным числом, значение numeric_expression округляется слева от десятичной запятой, как указано в аргументе length.When length is a negative number, numeric_expression is rounded on the left side of the decimal point, as specified by length.
functionfunctionТип выполняемой операции.Is the type of operation to perform. Аргумент function должен иметь тип tinyint, smallint или int. Если аргумент function не указан или имеет значение 0 (по умолчанию), значение numeric_expression округляется.function must be tinyint, smallint, or int. When function is omitted or has a value of 0 (default), numeric_expression is rounded. Когда указывается значение, не равное 0, значение numeric_expression усекается.When a value other than 0 is specified, numeric_expression is truncated.
Итого
Чтобы писать числа с большим количеством нулей:
- Используйте краткую форму записи чисел – , с указанным количеством нулей. Например: это с 6-ю нулями .
- Отрицательное число после приводит к делению числа на 1 с указанным количеством нулей. Например: это ( миллионных).
Для других систем счисления:
- Можно записывать числа сразу в шестнадцатеричной (), восьмеричной () и бинарной () системах счисления
- преобразует строку в целое число в соответствии с указанной системой счисления: .
- представляет число в строковом виде в указанной системе счисления .
Для преобразования значений типа и в число:
Используйте parseInt/parseFloat для «мягкого» преобразования строки в число, данные функции по порядку считывают число из строки до тех пор пока не возникнет ошибка.
Для дробей:
- Используйте округления , , , или .
- Помните, что при работе с дробями происходит потеря точности.
Ещё больше математических функций:
Документация по объекту Math
Библиотека маленькая, но содержит всё самое важное