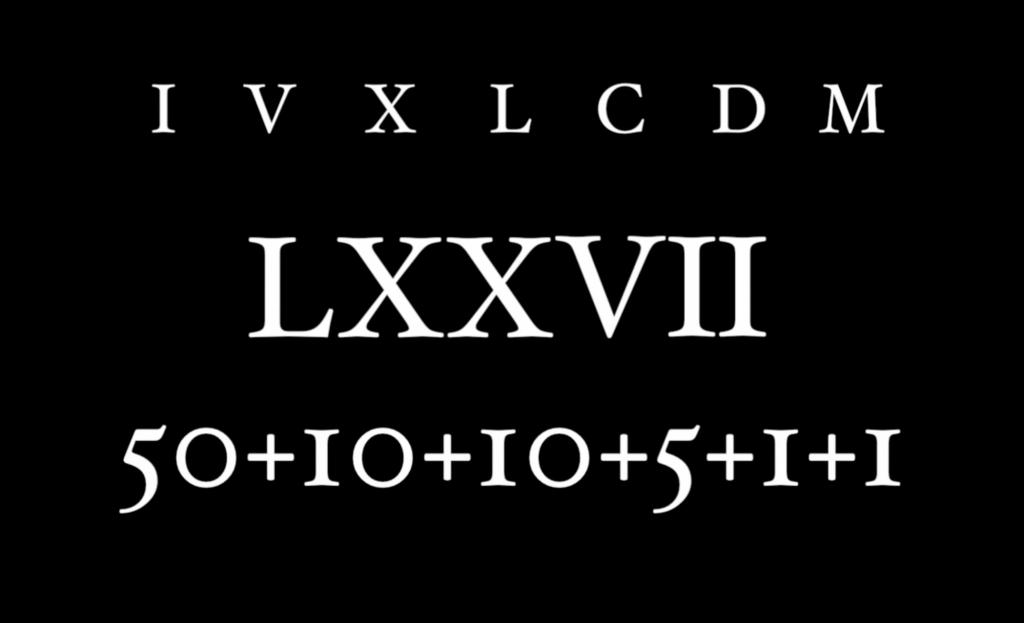Почему цифры называются арабскими: история
Содержание:
- Применение
- История
- Написание
- Использование нуля в расчетах
- ПОЛЕЗНЫЙ АРАБСКИЙ – СЧИТАЕМ ПО-ЕГИПЕТСКИ. ВСЁ О ЦИФРАХ.
- Порядковые
- История появления арабских цифр
- Откуда взялись современные числовые знаки от 1 до 10
- Откуда взялись современные числовые знаки от 1 до 10
- Преимущества индоарабских цифр
- Применение[править | править код]
- С помощью ALT-кода
Применение
Автограф Б. Н. Ельцина 10 ноября 1988 года. Месяц указан римскими цифрами.
Римские цифры, обозначающие день недели, на витрине одного из магазинов в Вильнюсе
В русском языке римские цифры используются в следующих случаях:
- Номер века или тысячелетия: XIX век, II тысячелетие до н. э.
- Спряжение глагола
- Порядковый номер монарха.
- Номер корпуса в Вооружённых силах.
- Группа крови на нашивках формы военнослужащих ВС РФ.
- Номер тома в многотомной книге (иногда — номера частей книги, разделов или глав).
- В некоторых изданиях — номера листов с предисловием к книге, чтобы не исправлять ссылки внутри основного текста при изменении предисловия.
- Маркировка циферблатов часов «под старину».
- Иные важные события или пункты списка, например: V постулат Евклида, II мировая война, XX съезд КПСС, Игры XXII Олимпиады и тому подобное.
- Валентность химических элементов.
- Порядковый номер ступени в звукоряде.
- База гомеопатических разведений (Conium X3, Aconitum C200 и тому подобное).
- В математическом анализе римскими цифрами записывается номер производной, правда, при чтении (обычно) произносится «штрих» вместо I, «два штриха» вместо II, «три штриха» вместо III. Наконец, начиная с IV, читается «четвёртая производная»: f′(x)=fI(x)=f(1)(x){\displaystyle f'(x)=f^{I}(x)=f^{(1)}(x)}, но fIV(x)=f(4)(x){\displaystyle f^{IV}(x)=f^{(4)}(x)}.
Римские цифры широко употреблялись в СССР при указании даты для обозначения месяца года, например: 11/III-85 или 9.XI.89, это можно увидеть на многих архивных документах тех времён. Подобным образом, через косую черту, в том числе записывали дату урока в классных журналах, например: 24/II. Для указания дат жизни и смерти на надгробиях часто использовался особый формат, где месяц года также обозначался римскими цифрами, например: 186XII78∼195III53{\displaystyle 18{\frac {6}{XII}}78\sim 19{\frac {5}{III}}53}. Подобный формат в 1970-1980-х годах использовался в медицинских справках.[источник не указан 432 дня]
С переходом на компьютерную обработку информации форматы даты, основанные на римских цифрах, практически вышли из употребления.
В других языках сфера применения римских цифр может иметь особенности. В западных странах римскими цифрами нередко записывается номер года, например, на фронтонах зданий и в титрах кино- и видеопродукции.
В современной Литве на дорожных знаках, на витринах магазинов, на вывесках предприятий римскими цифрами могут обозначаться дни недели.
История
Первое обнаруженное появление нуля — IX век, Индия
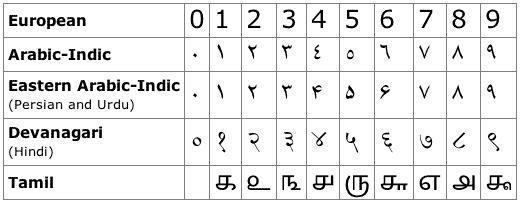
1) «Современные цифры» — обычные арабские цифры. «Арабские цифры» — индо-арабские и персидские цифры. Цифры 4, 5 и 6 существуют в двух вариантах, слева — индо-арабский, справа — персидский. «Индийские цифры» — цифры деванагари современной Индии.
Первая дошедшая до наших дней запись в десятичной позиционной системе относится к 595 году н. э. Отдельного знака для нуля сначала у индийцев не было, вместо него оставляли пустое место. Символ нуля (шунья) окончательно оформился в IX веке.
Преимущества индийской системы записи для арифметических расчётов вскоре оценили персы и арабы. Индийские цифры активно популяризировал в IX веке при дворе халифа аль-Мансура в Багдаде хорезмиец Аль-Хорезми, автор знаменитой работы «Китаб аль-джебр ва-ль-мукабала», от названия которой произошёл термин «алгебра». Аль-Хорезми написал книгу «Об индийском счёте», которая способствовала популяризации десятичной позиционной системы записи чисел во всём Халифате, вплоть до мусульманской Испании.
Сохранились трактат математика Ас-Сиджизи, датированный 969 годом, и копия трактата астронома Аль-Бируни, датированная 1082 годом, содержащие индийские цифры.
В современных арабских странах Азии, а также в Египте, Иране, Пакистане и Афганистане, в основном, используются цифры, мало отличающиеся от имеющихся в труде аль-Бируни. Арабы называют их «ар-кам хиндия» (أَرْقَام هِنْدِيَّة) — «индийские цифры», но европейцы чаще называют их «индо-арабскими» и «персидскими», так как в языках народов современной Индии цифры эволюционировали и теперь сильно отличаются от средневековых индийских цифр. Позднее их начертания продолжали изменяться, и в трактате западноафриканского математика Ибн аль-Банна аль-Марракуши (XIII век) уже все цифры походили на нынешние европейские (хотя четвёрка и пятёрка были повёрнуты на 90 градусов). В современных арабских странах Африки (кроме Египта) используются те же цифры, что и в Европе.
Арабские цифры стали известны европейцам в X веке. Первое их описание содержит «Вигиланский кодекс» (Испания, X век), причём ноль ещё не упоминается. В других странах Западной Европы история индоарабских цифр начинается с XII века, а их широкое применение в Западной Европе — с XIII—XIV веков.
В XII веке книга Аль-Хорезми «Об индийском счёте» была переведена Робертом Честерским на латинский язык и сыграла очень большую роль в развитии европейской арифметики и внедрении арабских цифр.
После отвоевания Испании контакты европейцев с арабами ослабли, и многие европейцы по-прежнему использовали римские цифры
Итальянский математик Фибоначчи, изучавший в 1192—1200 годах математику в Алжире и других арабских странах, снова привлёк внимание европейцев к арабским цифрам, написав «Книгу абака». В эпоху Возрождения возрос интерес к арабской науке, итальянские математики привозили в Европу арабские рукописи
Ко времени распространения книгопечатания в западноевропейской науке укоренилось западно-арабское начертание цифр.
В России арабские цифры появились в XIV—XV вв., широкое распространение получили с XVII в., а после введения гражданской азбуки в XVIII в. вытеснили из гражданской печати славяно-кирилловские цифры.
Написание
Как выглядят арабские цифры? Раньше они были составлены из обрывистых линий, где число углов сопоставлялось с величиной знака. Скорее всего, арабские математики высказали мысль о том, что можно связать количество углов с числовым значением цифры. Если посмотреть на старинное написание, то видно, какую величину имеют арабские цифры. Это какие же способности были у ученых в такое древнее время?
Итак, ноль не имеет углов в написании. Единица включает в себя лишь один острый угол. Двойка содержит пару острых углов. Тройка имеет три угла. Ее правильное арабское написание получается при вычерчивании почтового индекса на конвертах. Четверка включает в себя четыре угла, последний из которых создает хвостик. У пятерки пять прямых углов, а у шестерки, соответственно, шесть. При правильном старом написании семерка состоит из семи углов. Восьмерка – из восьми. А девятка, нетрудно догадаться, из девяти. Вот почему цифры называются арабскими: ими было придумано оригинальное начертание.
Использование нуля в расчетах
Детей в школе учат начинать отсчет с единицы. Но большинство программистов используют вычисления, где отсчет всегда начинается с нуля. Такая запись всех 10 чисел удобна тем, что для их представления используется только 1 символ. А экономия в программировании является неотъемлемой его частью. Если мы начнем отсчет с нуля, записывать цифру 10 нам не нужно. Её место занимает девятка.
Ноль обладает другими интересными свойствами при взаимодействии с числами. Так, если вы попытаетесь прибавить к нулю или отнять ноль от какого-нибудь числа — оно не изменится. Когда производится умножение на это число — вы получите 0 во всех случаях. При возведении каждого числа в ноль, получится единица. А также на ноль (0) нельзя разделить другое целое или дробное число.
Существует Закон Бенфорда. Если не вдаваться в подробности с рассмотрением формул и таблиц, он гласит, что в реальной жизни цифры от 1 до 4 встретить гораздо вероятнее, чем цифры от 5 до 9. Сюда можно отнести номера домов улиц, различную статистику и тому подобное. Есть у этого закона и практическое применение. Используя его, можно проверять бухгалтерские отчетности, результаты голосований, подсчет расходов.
В некоторых американских штатах несоответствие каких-либо расчетов по Закону Бенфорда является уликой, имеющей вес в судебном процессе. Все расчеты по этому закону производятся в десятичной системе. Таким образом, арабские цифры в границе от 1 до 10 являются самыми распространенными во всем мире.
ПОЛЕЗНЫЙ АРАБСКИЙ – СЧИТАЕМ ПО-ЕГИПЕТСКИ. ВСЁ О ЦИФРАХ.
Май 21st, 2015 Valjard
Без цифр в Египте никуда. Они вам нужны будут и в магазинах, и на рынках, и в транспорте, и при оплате коммунальных услуг.
1. Десятки
10. عِشرين – двадцать. ٢٠
11. تلاتين – тридцать. ٣٠
12. اربعين – сорок. ٤٠
13. خمسين – пятьдесят. ٥٠
14. ستين – шестьдесят. ٦٠
15. سبعين – семьдесят. ٧٠
16. تمانين – восемьдесят. ٨٠
17. تسعين – девяносто. ٩٠

2. Двухзначные числа
Посмотрим, как произносятся двузначные цифры (c 20 до 100). Порядок – обратный привычному нам. Сначала читаются единицы, потом десятки. Между ними используется союз «и», который в Египетском диалекте произносится как или (по вашему желанию на выбор).
1. واحِد و عِشرين – двадцать один. Пишется: ٢١
2. اِتنين و عشرين – двадцать два. ٢٢
3. تلاتة و عشرين – двадцать три. ٢٣
4. اربعة و عشرين – двадцать четыре. ٢٤
5. خمسة و عشرين – двадцать пять. ٢٥
6. ستّة و عشرين – двадцать шесть. ٢٦
7. سبعة و عشرين – двадцать семь. ٢٧
8. تمانية و عشرين – двадцать восемь. ٢٨
9. تسعة و عشرين – двадцать девять. ٢٩
Все остальные двузначные цифры строятся по такому же принципу.

3. Сотни!
А теперь узнаем, как произносятся в Египетском диалекте сотни:
1. مِية – сто, 100. Пишется: ١٠٠
2. مِتين – двести, 200. ٢٠٠
3. تُلتُميّة – триста, 300. ٣٠٠
4. رثبعُميّة – четыреста, 400. ٤٠٠
5. خمسُمِيّة – пятьсот, 500. ٥٠٠
6. سُتُّميّة – шестьсот, 600. ٦٠٠
7. سُبعُمِيّة – семьсот, 700. ٧٠٠
8. تُمنُمِيّة – весомьсот, 800. ٨٠٠
9. تُسعُمِيّة – девятьсот, 900. ٩٠٠

4. Трехзначные числа
Обратим внимание, как читаются трехзначные числа. В них используется только один союз و
При этом порядок может прямым и частично прямым.
Начнем с чисел, состоящих из сотен и единиц. В этом случае порядок цифр прямой – сначала читаются сотни, потом единицы, соединённые союзом و – и:
1. مِيّة و واحِد – сто один. Пишется: ١٠١
2. مِيّة و اِتنين – сто два. ١٠٢
3. مِيّة و تلاتة – сто три. ١٠٣
4. مِيّة و ارْبعة – сто четыре. ١٠٤
5. مِيّة و خمْسة – сто пять. ١٠٥
6. مِيّة و سِتّة – сто шесть. ١٠٥
7. مِيّة و سبعة – сто семь. ١٠٧
8. مِيّة و تمانسة – сто восемь. ١٠٨
9. مِيّة و تسعة – сто девять. ١٠٩
Точно также обстоит дело с другими сотнями. Примеры:
10. مِتين و واحِد – двести один. ٢٠١
11. تُلتًمية و اِتنين – триста два. ٣٠٢
12. رُبعُميّة و خمْسة – четыреста пять. ٤٠٥
И так далее.

Цифры от 110 до 120, а также сотни с десятками читаются в прямом порядке.
Примеры:
1. مِيّة و حِداشر – сто одиннадцать. Пишется: ١١١
2. مِيّة و اِتناشر – сто двенадцать. ١١٢
3. مِتين و تلتاشر – двести тринадцать. ٢١٣
4. تُلتُميّة و اربعتاشر – триста четырнадцать. ٣١٤
5. رُبعُميّة و خمستاشر – четыреста пятнадцать. ٤١٥
6. خُمسُميّة وسِتّاشر – пятьсот шестнадцать. ٥١٦
7. سُتُّميّة و سبعتاشر – шестьсот семнадцать. ٦١٧
8. سُبعميّة و تمنتاشر – семьсот восемнадцать. ٧١٨
9. تُمنُميّة و تسعتاشر – восемьсот девятнадцать. ٨١٩
10. تُسعُميّة و عِشرين – девятьсот двадцать. ٩٢٠
11. مِيّة و تلاتين – сто тридцать. ١٣٠
12. مِتين و اربعين – двести сорок.٢٤٠
13. تُلتُمِيّة و خمسين – триста пятьдесят. ٣٥٠
14. سُتُّمِيّة و سِتّين – шестьсот шестьдесят. ٦٦٠
Сотни с десятками и единицами читаются смешанно – в прямом и обратном порядке. Сначала произносятся сотни, потом единицы, потом союз و , который переводится как «и», затем десятки. Между сотнями и единицами союз و не используется.
Примеры подобных цифр:
1. مِية واحِد و عِشرين – сто двадцать один. Пишется: ١٢١
2. مِية خمْسة و تلاتين – сто тридцать пять. ١٣٥
3. متين تلاتة و عِشرين – двести двадцать три. ٢٢٣
4. تُلْتُميّة اِتنين و ارْبعين – триста сорок два. ٣٤٢
5. رُبعميّة ارْبعة و خمسين – четыреста пятьдесят четыре. ٤٥٤
6. خُمسُميّة سِتّة و سِتين – пятьсот шестьдесят шесть. ٥٦٦
7. سُبعميّة سبعة و سبعين – семьсот семьдесят семь. ٧٧٧
8. تُمنُميّة خمسة و تِسعين – восемьсот девяносто пять. ٨٩٥
9. تُسعُميّة تِسعة و تمانين – девятьсот восемьдесят девять. ٩٨٩
10. الْف – тысяча.١٠٠٠

5. Двойственное число
В отличие от русского языка, в египетском диалекте есть двойственное число, которое означает «два предмета». Образуется оно для существительного мужского рода присоединением к слову окончания ين , для существительного женского рода – добавлением окончания تين .
Примеры двойственного числа для слов мужского рода:
1.مكْتب офис, مكتبين – два офиса.
2.مفتاح – ключ, مفتاحين – два ключа.
3. شهر – месяц, شهرين – два месяца.
Обратите внимание! Нельзя говорить:
اِتنين مكتب .
Однако допустимо использование числительного اِتنين после существительного в двойственном числе. Пример: اِتنين مكتبين – два офиса
Примеры двойственного числа для слов женского рода:
4. عربية – машина, عربيتين – две машины.
5. شنْطة – сумка, سنْطتين – две сумки.
6. سنة – год, سنتين – два года.

Опубликовано в рубрике Египетский диалект Метки: арабский, Египет, Числа
ссылку
Порядковые
| Первый | — | Про́тос |
| Второй | — | Дэ́фтэрос |
| Третий | — | Три́тос |
| Четвёртый | — | Тэ́тартос |
| Пятый | — | Пэ́мптос |
| Шестой | — | Э́ктос |
| Седьмой | — | Э́вдомос |
| Восьмой | — | О́кдоос |
| Девятый | — | Э́натос |
| Десятый | — | Дэ́катос |
| Одиннадцатый | — | Эндэ́катос |
| Двенадцатый | — | Додэ́катос |
| Тринадцатый | — | Дэ́катос три́тос |
| Четырнадцатый | — | Дэ́катос тэ́тартос |
| Пятнадцатый | — | Дэ́катос пэ́мптос |
| Шестнадцатый | — | Дэ́катос э́ктос |
| Семнадцатый | — | Дэ́катос э́вдомос |
| Восемнадцатый | — | Дэ́катос о́гдоос |
| Девятнадцатый | — | Дэ́катос э́натос |
| Двадцатый | — | Икост́с |
| Двадцать первый | — | Ико́стос про́отос |
| Тридцатый | — | Триакосто́с |
| Сороковой | — | Тэсаракосто́с |
| Пятидесятый | — | Пэндыкосто́с |
| Шестидесятый | — | Ксикосто́с |
| Семидесятый | — | Эвдомикосто́с |
| Восьмидесятый | — | огдоикостос |
| Девяностый | — | Энэникосто́с |
| Сотый | — | Экатосто́с |
| Двухсотый | — | Дъякосиосто́с |
| Трёхсотый | — | Триакосиосто́с |
| Тысячный | — | Хилиосто́с |
История появления арабских цифр
Арабские числовые знаки были выдуманы и записаны в Индии, произошло это около 5 века. В это время был определен отсчет чисел при перечислении. Отправной точкой был ноль (оригинальное название шунья). Это число позволило сформировать нынешний порядок чисел при счете. Популяризацией арабских цифр занимался индийский ученый того времени Абу Аль-Хорезми, который создал несколько книг на эту тему. От одной из них произошло сегодняшнее название школьного предмета — алгебра. Предоставленный ученым способ записи числовых значений использовал десятичную систему.
Археологи находили разные работы древних математиков и археологов, которые использовали арабские цифры для своих работ. Эти работы были созданы предположительно в 8-9 веке. Сегодня большинство арабских стран используют отличительную от привычной всем записи чисел в европейских и других регионах. Более того, на Востоке принято писать порядок чисел с права налево.
Существует множество мнений, что в формировании цифр арабского происхождения, которыми пользуемся сегодня мы — 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, были использованы не только арабские цифры древней Индии. Посмотрев на таблицу арабских цифр в диапазоне от 1 до 10 старого и нового представления, можно найти множество сходств. Например, 1, 2, 3, 4 в начальном представлении — это те же знаки, только повернутые на 90 градусов.
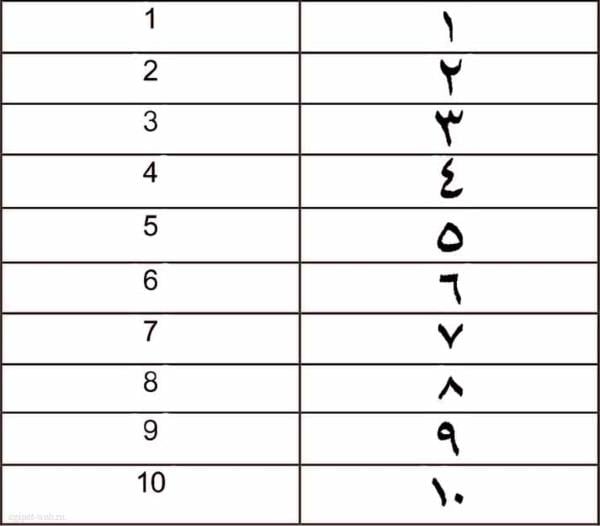
Откуда взялись современные числовые знаки от 1 до 10
Зарождение арабских цифр относят к древней южной Индии. Во многих древних странах, когда еще не было письма, использовались для счета палочки. Одна палочка обозначала 1, две — 2 и так далее. Такой способ записи навеян зарубками. Именно отсюда и происходят числа в римском представлении (для цифр 1, 2, 3). Индийские цифры позаимствовали некоторые элементы буквы из разных стран того времени.
 Скриншот арабских цифр от 1 до 100
Скриншот арабских цифр от 1 до 100
В цифрах встречаются признаки букв арамейского, греческого и финикийского алфавитов. Предположительно числовые знаки начали зарождаться во 2 веке до нашей эры, в то время, когда существовало Индо-греческое царство.
В отличие от счета в русском языке — один (1), два (2), три (3), арабские цифры имеют свое название:
- 1 (один) — 1 Уахид;
- 2 (два) — 2 Итнан;
- 3 (три) — 3 Талата;
- 4 (четыре) — 4 Арба-а;
- 5 (пять) — 5 Хамиза;
- 6 (шесть) — 6 Ситта;
- 7 (семь) — 7 Саба-а;
- 8 (восемь) — 8 Таманиа;
- 9 (девять) — 9 Тизза;
- 10 (десять) — 10 Ашара.
Откуда взялись современные числовые знаки от 1 до 10
Зарождение арабских цифр относят к древней южной Индии. Во многих древних странах, когда еще не было письма, использовались для счета палочки. Одна палочка обозначала 1, две — 2 и так далее. Такой способ записи навеян зарубками. Именно отсюда и происходят числа в римском представлении (для цифр 1, 2, 3). Индийские цифры позаимствовали некоторые элементы буквы из разных стран того времени.

В цифрах встречаются признаки букв арамейского, греческого и финикийского алфавитов. Предположительно числовые знаки начали зарождаться во 2 веке до нашей эры, в то время, когда существовало Индо-греческое царство.
В отличие от счета в русском языке — один (1), два (2), три (3), арабские цифры имеют свое название:
- 1 (один) — 1 Уахид;
- 2 (два) — 2 Итнан;
- 3 (три) — 3 Талата;
- 4 (четыре) — 4 Арба-а;
- 5 (пять) — 5 Хамиза;
- 6 (шесть) — 6 Ситта;
- 7 (семь) — 7 Саба-а;
- 8 (восемь) — 8 Таманиа;
- 9 (девять) — 9 Тизза;
- 10 (десять) — 10 Ашара.
Преимущества индоарабских цифр
Реализованная с помощью индоарабских цифр десятичная позиционная система счисления постепенно вытеснила римские цифры и другие непозиционные системы нумерации благодаря множеству несомненных преимуществ.
- Индийская запись чисел компактнее римской и позволяет быстро сравнивать разные числа по величине.
- При расчётах на абаке можно одновременно записывать числа и проводить расчёты.
- Вычисления стало возможно проводить без абака, на бумаге. Появились новые, более простые методы умножения и деления, специально рассчитанные на индоарабские цифры.
- Вычислительная математика и математика вообще получили мощный импульс к развитию. Например, трудно представить изобретение логарифмов без индоарабских цифр.
- Появилась возможность создания счётных машин.
Применение[править | править код]
Автограф Б. Н. Ельцина 10 ноября 1988 года. Месяц указан римскими цифрами.
Римские цифры, обозначающие день недели, на витрине одного из магазинов в Вильнюсе
В русском языке римские цифры используются в следующих случаях:
- Номер века или тысячелетия: XIX век, II тысячелетие до н. э.
- Спряжение глаголов.
- Порядковый номер монарха.
- Номер корпуса в Вооружённых силах.
- Группа крови на нашивках формы военнослужащих ВС РФ.
- Номер тома в многотомной книге или тома журналов (иногда — номера частей книги, разделов или глав).
- В некоторых изданиях — номера листов с предисловием к книге, чтобы не исправлять ссылки внутри основного текста при изменении предисловия.
- Маркировка циферблатов часов «под старину».
- Иные важные события или пункты списка, например: V постулат Евклида, II мировая война, XX съезд КПСС, Игры XXII Олимпиады и тому подобное.
- Валентность химических элементов.
- Порядковый номер ступени в звукоряде.
- В математическом анализе римскими цифрами записывается номер производной, правда, при чтении (обычно) произносится «штрих» вместо I, «два штриха» вместо II, «три штриха» вместо III. Наконец, начиная с IV, читается «четвёртая производная»: f′(x)=fI(x)=f(1)(x){\displaystyle f'(x)=f^{I}(x)=f^{(1)}(x)}, но fIV(x)=f(4)(x){\displaystyle f^{IV}(x)=f^{(4)}(x)}.
Римские цифры широко употреблялись в СССР при указании даты для обозначения месяца года, например: 11/III-85 или 9.XI.89, это можно увидеть на многих архивных документах тех времён. Подобным образом, через косую черту, в том числе записывали дату урока в классных журналах, например: 24/II. Для указания дат жизни и смерти на надгробиях часто использовался особый формат, где месяц года также обозначался римскими цифрами, например: 1825XI87∼1926I43{\displaystyle 18{\textstyle {\frac {25}{XI}}}87\sim 19{\textstyle {\frac {26}{I}}}43} (25 ноября 1887 ~ 26 января 1943). Подобный формат в 1970-1980-х годах использовался в медицинских справках.[источник не указан 1346 дней]
С переходом на компьютерную обработку информации форматы даты, основанные на римских цифрах, практически вышли из употребления.
В других языках сфера применения римских цифр может иметь особенности. В западных странах римскими цифрами нередко записывается номер года, например, на фронтонах зданий и в титрах видео-, кино- и телепродукции.
В современной Литве на дорожных знаках, на витринах магазинов, на вывесках предприятий римскими цифрами могут обозначаться дни недели.
С помощью ALT-кода
Сейчас рассмотрим еще один способ, как вставить римские цифры в «Ворде» с помощью кода. Только на этот раз код называется ALT-код. Суть практически такая же, как и в предыдущем способе, но все же есть некоторые отличия, о которых сейчас поговорим.
Во-первых, сам код каждой цифры другой, во-вторых, вводить его необходимо совсем иначе.
Для начала давайте перечислим сами коды и цифры им соответствующие:
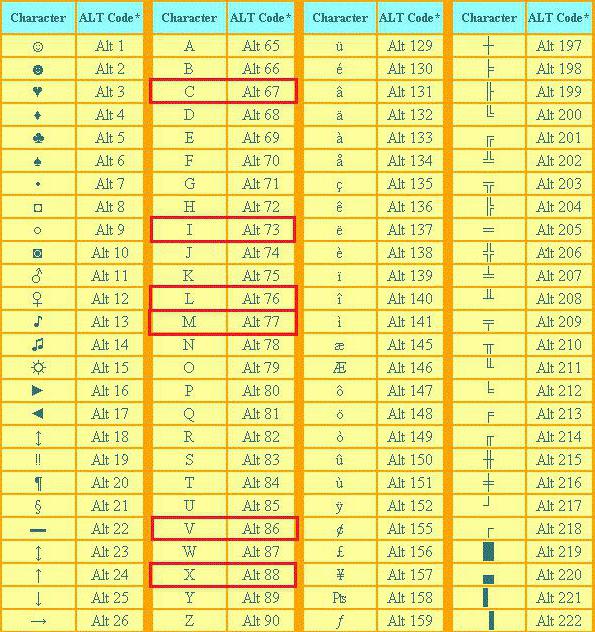
- 73 — I.
- 88 — X.
- 86 — V.
- 77 — M.
- 67 — C.
- 76 — L.
Итак, код мы знаем, осталось лишь его ввести. Для этого, зажав клавишу ALT, начните вводить код. После того как вы отпустите ALT, появится нужная вам цифра, соответствующая введенному вами коду
Обратите внимание, что код необходимо набирать на цифровой клавиатуре, расположенной справа
В некоторых типах документов возникает необходимость проставить нумерацию римскими цифрами. Особенно актуально и часто нумеруется таким способом века. Чтобы данная проблема не возникала в дальнейшем, я в данной статье расскажу два способа как поставить римские цифры в ворде.
Самый простой способ можно часто использовать для указания года, века или тысячелетия. Эти значения цифр представляют собой небольшие значения и их можно легко напечатать используя латинские буквы в заглавном исполнении (1) — I, (5) — V, (10) — X, (50) — L, (100) — C, (500) — D, (1000) — M. Использую ниже таблицу соответствия арабских цифр римским можно легко понять как формировать число вплоть до нескольких тысяч.
| 1 | I | 26 | XXVI | 51 | LI | 76 | LXXVI |
| 2 | II | 27 | XXVII | 52 | LII | 77 | LXXVII |
| 3 | III | 28 | XXVIII | 53 | LIII | 78 | LXXVIII |
| 4 | IV | 29 | XXIX | 54 | LIV | 79 | LXXIX |
| 5 | V | 30 | XXX | 55 | LV | 80 | LXXX |
| 6 | VI | 31 | XXXI | 56 | LVI | 81 | LXXXI |
| 7 | VII | 32 | XXXII | 57 | LVII | 82 | LXXXII |
| 8 | VIII | 33 | XXXIII | 58 | LVIII | 83 | LXXXIII |
| 9 | IX | 34 | XXXIV | 59 | LIX | 84 | LXXXIV |
| 10 | X | 35 | XXXV | 60 | LX | 85 | LXXXV |
| 11 | XI | 36 | XXXVI | 61 | LXI | 86 | LXXXVI |
| 12 | XII | 37 | XXXVII | 62 | LXII | 87 | LXXXVII |
| 13 | XIII | 38 | XXXVIII | 63 | LXIII | 88 | LXXXVIII |
| 14 | XIV | 39 | XXXIX | 64 | LXIV | 89 | LXXXIX |
| 15 | XV | 40 | XL | 65 | LXV | 90 | XC |
| 16 | XVI | 41 | XLI | 66 | LXVI | 91 | XCI |
| 17 | XVII | 42 | XLII | 67 | LXVII | 92 | XCII |
| 18 | XVIII | 43 | XLIII | 68 | LXVIII | 93 | XCIII |
| 19 | XIX | 44 | XLIV | 69 | LXIX | 94 | XCIV |
| 20 | XX | 45 | XLV | 70 | LXX | 95 | XCV |
| 21 | XXI | 46 | XLVI | 71 | LXXI | 96 | XCVI |
| 22 | XXII | 47 | XLVII | 72 | LXXII | 97 | XCVII |
| 23 | XXIII | 48 | XLVIII | 73 | LXXIII | 98 | XCVIII |
| 24 | XXIV | 49 | XLIX | 74 | LXXIV | 99 | XCIX |
| 25 | XXV | 50 | L | 75 | LXXV | 100 | C |
Чтобы поставить в Word большие значения чисел в римском исполнении и если их необходимо к тому же напечатать много, можно очень легко запутаться и сделать ошибку. Для таких целей в программе Word предусмотрен блок для ввода формул, который называется «Поле». В поле можно написать формулу преобразования арабского числа в римское и программа автоматически напечатает нужный нам результат.
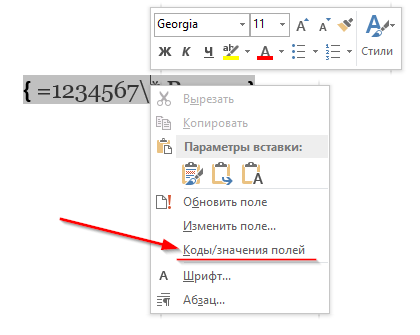
Чтобы преобразовать число в римское, поставьте курсор в месте, где необходимо напечатать римское число и нажмите сочетание клавиш Ctrl+F9. В месте курсора появиться специальный символ вставки поля в виде фигурных скобок. Внутри скобок введите следующую формулу (вместо числа 1234567 введите свое число для преобразования) и нажмите Ок:

Эта формула преобразует число 1234567 в римское. Чтобы отобразить не формулу, а значение результата преобразования, необходимо нажать F9 или же нажать правой кнопкой мыши на формуле и в контексте выбрать «Коды/значения полей».
Вместо формулы у вас должно появиться число в формате римских цифр. Для числа 1234567 у меня выдало следующее: