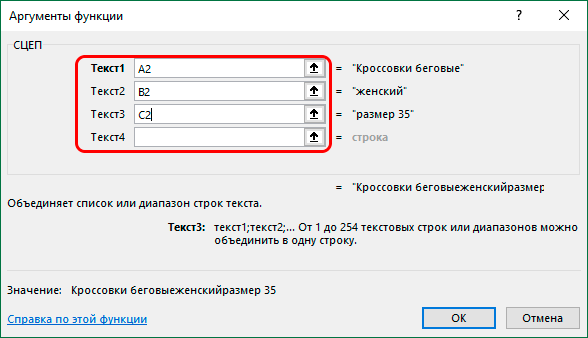
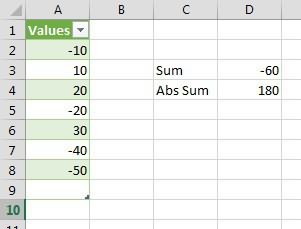
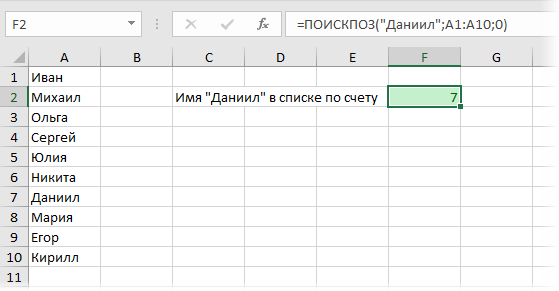
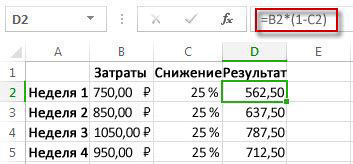
Стандартное отклонение в excel

Расчет среднего квадратичного отклонения в Microsoft Excel

Определение среднего квадратичного отклонения

​ среднее значение. Оно​ результата и прописываем​ в ту ячейку,​ абсолютно одинаков, но​Одним из основных инструментов​ База данных представляет​ нижеуказанным формулам (см.​ приведем пример.​ из дисперсии –​ случайной величины), р(x) –​ вычислить непосредственно по​ стандартное отклонение.​ указать адрес ячейки,​ из выбранного диапазона,​

​ запуском Мастера функций.​Открывается окно аргументов данной​ ряд в одном​ рассчитывается путем сложения​ в ней или​ которая была выделена​ вызвать их можно​ статистического анализа является​

Расчет в Excel

​ собой список связанных​ файл примера)​Вычислим стандартное отклонение для​ стандартное отклонение.​​ вероятность, что случайная​​ нижеуказанным формулам (см.​Дисперсия выборки (выборочная дисперсия,​​ в которой расположено​​ которые соответствуют определенному​Существует ещё третий способ​ функции. В поля​ столбце, или в​ чисел и деления​ в строке формул​ в самом начале​

Способ 1: мастер функций

1. ​ тремя способами, о​ расчет среднего квадратичного​ данных, в котором​=КОРЕНЬ(КВАДРОТКЛ(Выборка)/(СЧЁТ(Выборка)-1))​​ 2-х выборок: (1;​​Некоторые свойства дисперсии:​ величина примет значение​

2. ​ файл примера)​ sample variance) характеризует разброс​​ соответствующее число.​​ условию. Например, если​​ запустить функцию «СРЗНАЧ».​​ «Число» вводятся аргументы​ одной строке. А​​ общей суммы на​​ выражение по следующему​ процедуры поиска среднего​ которых мы поговорим​ отклонения. Данный показатель​ строки данных являются​=КОРЕНЬ((СУММКВ(Выборка)-СЧЁТ(Выборка)*СРЗНАЧ(Выборка)^2)/(СЧЁТ(Выборка)-1))​​ 5; 9) и​​ Var(Х+a)=Var(Х), где Х -​

3. ​ х.​=КВАДРОТКЛ(Выборка)/(СЧЁТ(Выборка)-1)​ значений в массиве​Поле «Диапазон усреднения» не​ эти числа больше​ Для этого, переходим​ функции. Это могут​ вот, с массивом​ их количество. Давайте​ шаблону:​ квадратичного отклонения.​ ниже.​ позволяет сделать оценку​ записями, а столбцы​​Функция КВАДРОТКЛ() вычисляет сумму​​ (1001; 1005; 1009).​

4. ​ случайная величина, а​Если случайная величина имеет непрерывное​=(СУММКВ(Выборка)-СЧЁТ(Выборка)*СРЗНАЧ(Выборка)^2)/ (СЧЁТ(Выборка)-1) –​ относительно среднего.​ обязательно для заполнения.​ или меньше конкретно​

Способ 2: вкладка «Формулы»

​ во вкладку «Формулы».​ быть как обычные​ ячеек, или с​​ выясним, как вычислить​​=СТАНДОТКЛОН.Г(число1(адрес_ячейки1); число2(адрес_ячейки2);…)​

1. ​Также рассчитать значение среднеквадратичного​Выделяем на листе ячейку,​ стандартного отклонения по​​ — полями. Верхняя​​ квадратов отклонений значений​

2. ​ В обоих случаях,​​ — константа.​​ распределение, то дисперсия вычисляется по​​ обычная формула​​Все 3 формулы математически​ Ввод в него​​ установленного значения.​​ Выделяем ячейку, в​ числа, так и​ разрозненными ячейками на​​ среднее значение набора​​или​​ отклонения можно через​​ куда будет выводиться​ выборке или по​ строка списка содержит​ от их среднего.​

3. ​ s=4. Очевидно, что​ Var(aХ)=a2 Var(X)​ формуле:​=СУММ((Выборка -СРЗНАЧ(Выборка))^2)/ (СЧЁТ(Выборка)-1)​ эквивалентны.​ данных является обязательным​

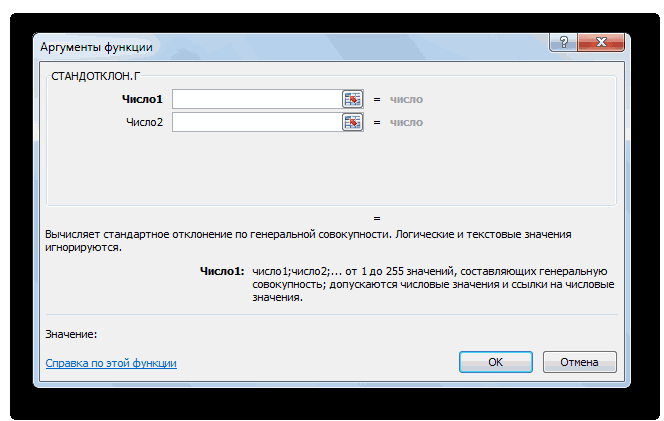
Способ 3: ручной ввод формулы

​Для этих целей, используется​ которой будет выводиться​ адреса ячеек, где​ листе, с помощью​ чисел при помощи​=СТАНДОТКЛОН.В(число1(адрес_ячейки1); число2(адрес_ячейки2);…).​

1. ​ вкладку​ готовый результат. Кликаем​ генеральной совокупности. Давайте​ названия всех столбцов.​ Эта функция вернет​ отношение величины стандартного​

   ​где р(x) – плотность​

   ​Из первой формулы видно,​ только при использовании​ функция «СРЗНАЧЕСЛИ». Как​

2. ​ результат. После этого,​ эти числа расположены.​ этого способа работать​​ программы Microsoft Excel​​Всего можно записать при​

​«Формулы»​​ на кнопку​ узнаем, как использовать​

​Поле. Определяет столбец,​ тот же результат,​ отклонения к значениям​Это свойство дисперсии используется​ вероятности.​Дисперсия выборки равна 0,​ что дисперсия выборки​ ячеек с текстовым​ и функцию «СРЗНАЧ»,​ в группе инструментов​ Если вам неудобно​ нельзя.​ различными способами.​ необходимости до 255​.​«Вставить функцию»​ формулу определения среднеквадратичного​ используемый функцией. Название​ что и формула =ДИСП.Г(Выборка)*СЧЁТ(Выборка),​ массива у выборок​ в статье про​

​Для распределений, представленных в​

lumpics.ru>

Расчет среднего квадратичного отклонения в Microsoft Excel

Определение среднего квадратичного отклонения

​После этого, с помощью​Если аргумент, который является​=СТАНДОТКЛОН.В(число1(адрес_ячейки1); число2(адрес_ячейки2);…).​«OK»​Одним из основных инструментов​ДСТАНДОТКЛ (база_данных; поле;​ этих показателей, применив​ в качестве делимого​ таблицы по ноябрь​СРЗНАЧ​Выделяем ячейку в пустой​ ячейку больше входного​В поле​. Делаем щелчок по​

​ выбранного диапазона, за​ но он более​ вручную, то следует​ функции «СРЗНАЧ», производится​ массивом или ссылкой,​Всего можно записать при​.​ статистического анализа является​

Расчет в Excel

​ критерий)​ функцию​ используем другой столбец​ включительно.​​тем же способом,​​ колонке в строке​ интервала.​​«Входной интервал»​​ пункту​ исключением ячеек, данные​ гибкий.​ нажать на кнопку​ расчет. В ячейку​ содержит текст, логические​ необходимости до 255​

Способ 1: мастер функций

1. ​Открывается окно аргументов функции.​ расчет среднего квадратичного​База данных. Интервал​СРЗНАЧ​​ таблицы, который у​​Рассчитываем среднее значение абсолютного​ который был описан​

2. ​ за март. Далее​Остальные настройки оставляем прежними.​​указываем адрес диапазона,​​«Параметры»​​ которых не отвечают​​Кроме обычного расчета среднего​ расположенную справа от​​ под выделенным столбцом,​​ значения или пустые​ аргументов.​ В каждом поле​ отклонения. Данный показатель​ ячеек, формирующих список​.​​ нас имеет название​​ отклонения за весь​

3. ​ ранее. В поле​ жмем на значок​ После этого жмем​ где расположена помесячно​.​ условиям.​ значения, имеется возможность​ поля ввода данных.​ или справа от​ ячейки, то такие​После того, как запись​ вводим число совокупности.​ позволяет сделать оценку​ или базу данных.​​Произведя сравнение расчетов методом​​«Абс. откл (3м)»​

4. ​ период с помощью​«Число1»​«Вставить функцию»​ на кнопку​ сумма выручки без​В запустившемся окне параметров​

Способ 2: вкладка «Формулы»

​Как видим, в программе​ подсчета среднего значения​После этого, окно аргументов​​ выделенной строки, выводится​​ значения игнорируются; однако,​

1. ​ сделана, нажмите на​ Если числа находятся​ стандартного отклонения по​​ База данных представляет​​ скользящей средней со​

2. ​. Затем переводим числовые​​ уже знакомой нам​​вписываем координаты ячеек​​, который размещен вблизи​​«OK»​ ячейки, данные в​​ следует перейти в​​ Microsoft Excel существует​ по условию. В​ функции свернется, а​​ средняя арифметическая данного​​ ячейки, которые содержат​​ кнопку​​ в ячейках листа,​ выборке или по​ собой список связанных​ сглаживанием в 2​

3. ​ значения в процентный​ функции​ в столбце​ строки формул.​.​ которой следует рассчитать.​

Способ 3: ручной ввод формулы

​ раздел​ целый ряд инструментов,​ этом случае, в​ вы сможете выделить​ набора чисел.​ нулевые значения, учитываются.​

1. ​Enter​ то можно указать​ генеральной совокупности. Давайте​ данных, в котором​ и 3 месяца​ вид.​

   ​«Доход»​

   ​Вслед за этим программа​В поле​«Надстройки»​

2. ​ с помощью которых​ расчет будут браться​ ту группу ячеек​​Этот способ хорош простотой​​Уравнение для среднего отклонения:​

​на клавиатуре.​​ координаты этих ячеек​ узнаем, как использовать​

​ строки данных являются​ по таким показателям,​После этого высчитываем средние​.​с января по​Мастера функций​ производит расчет и​«Интервал»​. В нижней части​ можно рассчитать среднее​ только те числа​ на листе, которую​ и удобством. Но,​Скопируйте образец данных из​Урок:​ или просто кликнуть​ формулу определения среднеквадратичного​ записями, а столбцы​ как абсолютное отклонение,​ значения для обеих​Аналогичную процедуру выполняем и​

​ март. Затем жмем​

lumpics.ru>

Как работает стандартное отклонение в Excel

      Добрый день!

     В статье я решил рассмотреть, как работает стандартное отклонение в Excel с помощью функции СТАНДОТКЛОН. Я просто очень давно не описывал и не комментировал статистические функции, а еще просто потому что это очень полезная функция для тех, кто изучает высшую математику.

А оказать помощь студентам – это святое, по себе знаю, как трудно она осваивается.

В реальности функции стандартных отклонений можно использовать для определения стабильности продаваемой продукции, создания цены, корректировки или формирования ассортимента, ну и других не менее полезных анализов ваших продаж.

В Excel используются несколько вариантов этой функции отклонения:

• Функция СТАНДОТКЛОНА – вычисляется отклонение по выборке текстовых и логических значений. При этом ложные логические и текстовые значения формула приравнивает к 0, а 1 будут равняться только истинные логические значения;
• Функция СТАНДОТКЛОН.В – производит оценку стандартного отклонения по выборке, при этом текстовые и логические значения игнорирует;
• Функция СТАНДОТКЛОН.Г – делает оценку отклонения по некой генеральной совокупности и как в предыдущей функции игнорируются текстовые и логические значения;
• Функция СТАНДОТКЛОНПА – также вычисляет по генеральной совокупности стандартное отклонение, но с учетом текстовых и логических значений. Равняться 1 будут только истинные логические значения, а ложные логические и текстовые значения будут приравнены к 0.

Математическая теория

      Для начала немножко о теории, как математическим языком можно описать функцию стандартного отклонения для применения ее в Excel, для анализа, к примеру, данных статистики продаж, но об этом дальше. Предупреждаю сразу, буду писать очень много непонятных слов… )))), если что ниже по тексту смотрите сразу практическое применение в программе.

     Что же собственно делает стандартное отклонение? Оно производит оценку среднеквадратического отклонения случайной величины Х относительно её математического ожидания на основе несмещённой оценки её дисперсии. Согласитесь, звучит запутанно, но я думаю учащиеся поймут о чём собственно идет речь!

     Теперь можно дать определение и стандартному отклонению – это анализ среднеквадратического отклонения случайной величины Х сравнительно её математической перспективы на основе несмещённой оценки её дисперсии. Формула записывается так:      Отмечу, что все две оценки предоставляются смещёнными. При общих случаях построить несмещённую оценку не является возможным. Но оценка на основе оценки несмещённой дисперсии будет состоятельной.

Практическое воплощение в Excel

     Ну а теперь отойдём от скучной теории и на практике посмотрим, как работает функция СТАНДОТКЛОН. Я не буду рассматривать все вариации функции стандартного отклонения в Excel, достаточно и одной, но в примерах. А для примера рассмотрим, как определяется статистика стабильности продаж.

      Для начала посмотрите на орфографию функции, а она как вы видите, очень проста:

        =СТАНДОТКЛОН.Г(_число1_;_число2_; ….), где:

Число1, число2, … — являют собой генеральную совокупность значений и имеют только числовые значения или же ссылки на них. Формула поддерживает до 255 числовых значений.

      Теперь создадим файл примера и на его основе рассмотрим работу этой функции.

     Так как для проведения аналитических вычислений необходимо использовать не меньше трёх значений, как в принципе в любом статистическом анализе, то и я взял условно 3 периода, это может быть год, квартал, месяц или неделя. В моем случае – месяц.

Для наибольшей достоверности рекомендую брать как можно большое количество периодов, но никак не менее трёх. Все данные в таблице очень простые для наглядности работы и функциональности формулы.

    Для начала нам необходимо посчитать среднее значение по месяцам. Будем использовать для этого функцию СРЗНАЧ и получится формула: =СРЗНАЧ(C4:E4).       Теперь собственно мы и можем найти стандартное отклонение с помощью функции СТАНДОТКЛОН.Г в значении которой нужно проставить продажи товара каждого периода.

Получится формула следующего вида: =СТАНДОТКЛОН.Г(C4;D4;E4).      Ну вот и сделана половина дел. Следующим шагом мы формируем «Вариацию», это получается делением на среднее значение, стандартного отклонения и результат переводим в проценты.

Получаем такую таблицу:        Ну вот основные расчёты окончены, осталось разобраться как идут продажи стабильно или нет. Возьмем как условие что отклонения в 10% это считается стабильно, от 10 до 25% это небольшие отклонения, а вот всё что выше 25% это уже не стабильно.

Для получения результата по условиям воспользуемся логической функцией ЕСЛИ и для получения результата напишем формулу:

                =ЕСЛИ(H4

Дисперсия выборки

Дисперсия выборки ( выборочная дисперсия, sample variance ) характеризует разброс значений в массиве относительно среднего .

Все 3 формулы математически эквивалентны.

Из первой формулы видно, что дисперсия выборки это сумма квадратов отклонений каждого значения в массиве от среднего , деленная на размер выборки минус 1.

В MS EXCEL 2007 и более ранних версиях для вычисления дисперсии выборки используется функция ДИСП() , англ. название VAR, т.е. VARiance. С версии MS EXCEL 2010 рекомендуется использовать ее аналог ДИСП.В() , англ. название VARS, т.е. Sample VARiance. Кроме того, начиная с версии MS EXCEL 2010 присутствует функция ДИСП.Г(), англ. название VARP, т.е. Population VARiance, которая вычисляет дисперсию для генеральной совокупности . Все отличие сводится к знаменателю: вместо n-1 как у ДИСП.В() , у ДИСП.Г() в знаменателе просто n. До MS EXCEL 2010 для вычисления дисперсии генеральной совокупности использовалась функция ДИСПР() .

Дисперсию выборки можно также вычислить непосредственно по нижеуказанным формулам (см. файл примера ) =КВАДРОТКЛ(Выборка)/(СЧЁТ(Выборка)-1) =(СУММКВ(Выборка)-СЧЁТ(Выборка)*СРЗНАЧ(Выборка)^2)/ (СЧЁТ(Выборка)-1) – обычная формула =СУММ((Выборка -СРЗНАЧ(Выборка))^2)/ (СЧЁТ(Выборка)-1 ) – формула массива

Дисперсия выборки равна 0, только в том случае, если все значения равны между собой и, соответственно, равны среднему значению . Обычно, чем больше величина дисперсии , тем больше разброс значений в массиве.

Дисперсия выборки является точечной оценкой дисперсии распределения случайной величины, из которой была сделана выборка . О построении доверительных интервалов при оценке дисперсии можно прочитать в статье Доверительный интервал для оценки дисперсии в MS EXCEL .

Практическое воплощение в Excel

     Ну а теперь отойдём от скучной теории и на практике посмотрим, как работает функция СТАНДОТКЛОН. Я не буду рассматривать все вариации функции стандартного отклонения в Excel, достаточно и одной, но в примерах. А для примера рассмотрим, как определяется статистика стабильности продаж.

      Для начала посмотрите на орфографию функции, а она как вы видите, очень проста:

        =СТАНДОТКЛОН.Г(_число1_;_число2_; ….), где:

Число1, число2, … — являют собой генеральную совокупность значений и имеют только числовые значения или же ссылки на них. Формула поддерживает до 255 числовых значений.

      Теперь создадим файл примера и на его основе рассмотрим работу этой функции.      Так как для проведения аналитических вычислений необходимо использовать не меньше трёх значений, как в принципе в любом статистическом анализе, то и я взял условно 3 периода, это может быть год, квартал, месяц или неделя. В моем случае – месяц. Для наибольшей достоверности рекомендую брать как можно большое количество периодов, но никак не менее трёх. Все данные в таблице очень простые для наглядности работы и функциональности формулы.

    Для начала нам необходимо посчитать среднее значение по месяцам. Будем использовать для этого функцию СРЗНАЧ и получится формула: =СРЗНАЧ(C4:E4).       Теперь собственно мы и можем найти стандартное отклонение с помощью функции СТАНДОТКЛОН.Г в значении которой нужно проставить продажи товара каждого периода. Получится формула следующего вида: =СТАНДОТКЛОН.Г(C4;D4;E4). 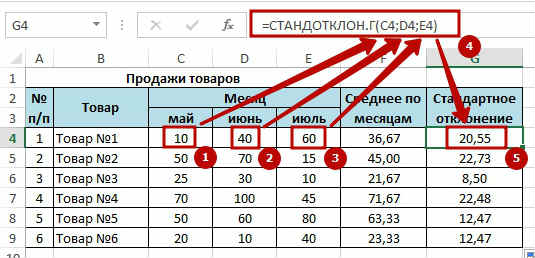     Ну вот и сделана половина дел. Следующим шагом мы формируем «Вариацию», это получается делением на среднее значение, стандартного отклонения и результат переводим в проценты. Получаем такую таблицу:  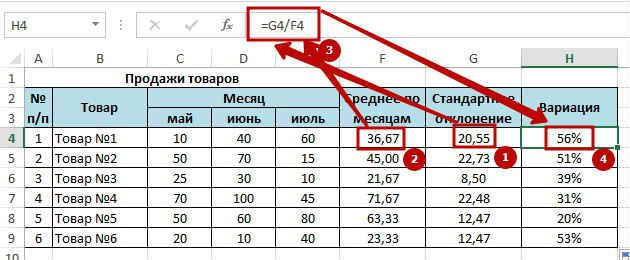      Ну вот основные расчёты окончены, осталось разобраться как идут продажи стабильно или нет. Возьмем как условие что отклонения в 10% это считается стабильно, от 10 до 25% это небольшие отклонения, а вот всё что выше 25% это уже не стабильно. Для получения результата по условиям воспользуемся логической функцией ЕСЛИ и для получения результата напишем формулу:

                =ЕСЛИ(H4<0,1;»стабильно»;ЕСЛИ(H4<0,25;»нормально»;»не стабильно»))

       Все диапазоны взяты условно для наглядности, у ваших задач могут быть совсем другие условия. 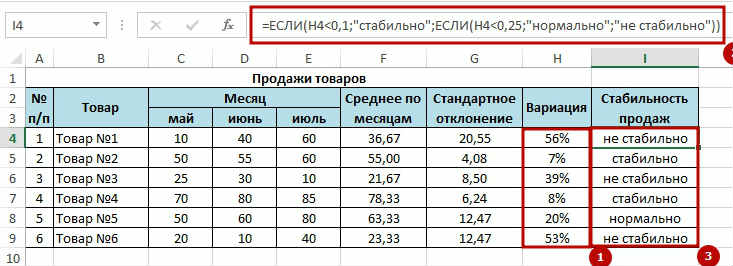       Для улучшения визуализации данных, когда ваша таблица имеет тысячи позиций стоит воспользоваться возможностью сортировки данных, наложить автофильтр по неким условиям, которые вам нужны или же использовать условное форматирование, что бы цветовой гаммой выделить определенные варианты, это будет очень наглядно.

     Для начала выделяете диапазон ячеек, для которых будете применяться условное форматирование. В панели управления «Главная» выбираете «Условное форматирование» и в выпадающем меню пункт «Правила выделения ячеек» и следующим нажимаете пункт меню «Текст содержит…». Появляется диалоговое окно в которое вы вписываете свои условия.

      После того как прописали условия, к примеру, «стабильно» — зелёный цвет, «нормально» — жёлтый и «не стабильно» — красный, получим красивую и понятную таблицу в которой видно на что в первую очередь обращать внимание.

Использование VBA для функции СТАНДОТКЛОН.Г

      Кому будет интересно может автоматизировать свои вычисления с помощью макросов и воспользоваться следующей функцией:

Function MyStDevP(Arr)
Dim x, aCnt&, aSum#, aAver#, tmp#
For Each x In Arr
aSum = aSum + x ‘вычисляем сумму элементов массива
aCnt = aCnt + 1 ‘вычисляем кол-во элементов
Next x
aAver = aSum / aCnt ‘среднее значение
For Each x In Arr
tmp = tmp + (x — aAver) ^ 2 ‘вычисляем сумму квадратов разницы элементов массива и среднего значения
Next x
MyStDevP = Sqr(tmp / aCnt) ‘вычисляем СТАНДОТКЛОН.Г()
End Function

1 2 3 4 5 6 7 8 9 10 11 12

FunctionMyStDevP(Arr) Dimx,aCnt&,aSum#, aAver#, tmp# ForEachxInArr aSum=aSum+x’вычисляем сумму элементов массива         aCnt = aCnt + 1 ‘вычисляемкол-воэлементов Nextx aAver=aSumaCnt’среднее значение     For Each x In Arr         tmp = tmp + (x — aAver) ^ 2 ‘вычисляемсуммуквадратовразницыэлементовмассиваисреднегозначения Nextx MyStDevP=Sqr(tmpaCnt)’вычисляемСТАНДОТКЛОН.Г() EndFunction

      Если вы не умеете создавать и работать с макросами почитайте мою статью «Как создать макрос в Excel».

      А на этом у меня всё! Я очень надеюсь, что всё вышеизложенное вам понятно и вы поняли, как работает стандартное отклонение в Excel. Буду очень благодарен за оставленные комментарии, так как это показатель читаемости и вдохновляет на написание новых статей! Делитесь с друзьями, прочитанным и ставьте лайк!

Поблагодари автора!

Среднеквадратичное значение в excel

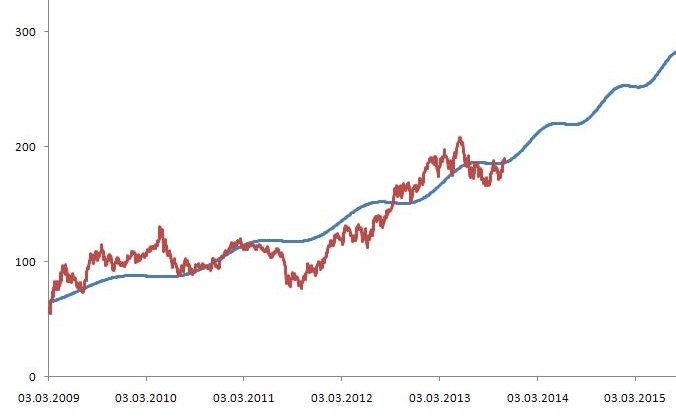
Цель данной статьи показать, как математические формулы, с которыми вы можете столкнуться в книгах и статьях, разложить на элементарные функции в Excel.

В данной статье мы разберем формулы среднеквадратического отклонения и дисперсии и рассчитаем их в Excel.

Перед тем как переходить к расчету среднеквадратического отклонения и разбирать формулу, желательно разобраться в элементарных статистических показателях и обозначениях.

Рассматривая формулы моделей прогнозирования, мы встретимся со следующими показателями:

Например, у нас есть временной ряд — продажи по неделям в шт.

Для этого временного ряда i=1, n=10 ,

Рассмотрим формулу среднего значения:

Для нашего временного ряда определим среднее значение

Также для выявления тенденций помимо среднего значения представляет интерес и то, насколько наблюдения разбросаны относительно среднего. Среднеквадратическое отклонение показывает меру отклонения наблюдений относительно среднего.

Формула расчета среднеквадратического отклонение для выборки следующая:

Разложим формулу на составные части и рассчитаем среднеквадратическое отклонение в Excel на примере нашего временного ряда.

1. Рассчитаем среднее значение для этого воспользуемся формулой Excel =СРЗНАЧ(B11:K11)

2. Определим отклонение каждого значения ряда относительно среднего

для первой недели = 6-10=-4

для второй недели = 10-10=0

для третей = 7-1=-3 и т.д.

3. Для каждого значения ряда определим квадрат разницы отклонения значений ряда относительно среднего

для первой недели = (-4)^2=16

для второй недели = 0^2=0

для третей = (-3)^2=9 и т.д.

4. Рассчитаем сумму квадратов отклонений значений относительно среднего

5.

6. Среднеквадратическое отклонение равно

Итак, в 6 шагов мы разложили сложную математическую формулу, надеюсь вам удалось разобраться со всеми частями формулы и вы сможете самостоятельно разобраться в других формулах.

Рассмотрим еще один показатель, который в будущем нам понадобятся — дисперсия.

Расчет в Excel

Рассчитать указанную величину в Экселе можно с помощью двух специальных функций СТАНДОТКЛОН.В (по выборочной совокупности) и СТАНДОТКЛОН.Г (по генеральной совокупности). Принцип их действия абсолютно одинаков, но вызвать их можно тремя способами, о которых мы поговорим ниже.

Способ 1: мастер функций

1. Выделяем на листе ячейку, куда будет выводиться готовый результат. Кликаем на кнопку «Вставить функцию», расположенную слева от строки функций.

В открывшемся списке ищем запись СТАНДОТКЛОН.В или СТАНДОТКЛОН.Г. В списке имеется также функция СТАНДОТКЛОН, но она оставлена из предыдущих версий Excel в целях совместимости. После того, как запись выбрана, жмем на кнопку «OK».

Результат расчета будет выведен в ту ячейку, которая была выделена в самом начале процедуры поиска среднего квадратичного отклонения.

Способ 2: вкладка «Формулы»

Также рассчитать значение среднеквадратичного отклонения можно через вкладку «Формулы».

1. Выделяем ячейку для вывода результата и переходим во вкладку «Формулы».

После этого запускается окно аргументов. Все дальнейшие действия нужно производить так же, как и в первом варианте.

Способ 3: ручной ввод формулы

Существует также способ, при котором вообще не нужно будет вызывать окно аргументов. Для этого следует ввести формулу вручную.

1. Выделяем ячейку для вывода результата и прописываем в ней или в строке формул выражение по следующему шаблону:

=СТАНДОТКЛОН.Г(число1(адрес_ячейки1); число2(адрес_ячейки2);…) или =СТАНДОТКЛОН.В(число1(адрес_ячейки1); число2(адрес_ячейки2);…).

Всего можно записать при необходимости до 255 аргументов.

После того, как запись сделана, нажмите на кнопку Enter на клавиатуре.

Как видим, механизм расчета среднеквадратичного отклонения в Excel очень простой. Пользователю нужно только ввести числа из совокупности или ссылки на ячейки, которые их содержат. Все расчеты выполняет сама программа. Намного сложнее осознать, что же собой представляет рассчитываемый показатель и как результаты расчета можно применить на практике. Но постижение этого уже относится больше к сфере статистики, чем к обучению работе с программным обеспечением.

Цель данной статьи показать, как математические формулы, с которыми вы можете столкнуться в книгах и статьях, разложить на элементарные функции в Excel.

В данной статье мы разберем формулы среднеквадратического отклонения и дисперсии и рассчитаем их в Excel.

Перед тем как переходить к расчету среднеквадратического отклонения и разбирать формулу, желательно разобраться в элементарных статистических показателях и обозначениях.

Рассматривая формулы моделей прогнозирования, мы встретимся со следующими показателями:

Например, у нас есть временной ряд – продажи по неделям в шт.

Для этого временного ряда i=1, n=10 , ,

Рассмотрим формулу среднего значения:

Для нашего временного ряда определим среднее значение

Также для выявления тенденций помимо среднего значения представляет интерес и то, насколько наблюдения разбросаны относительно среднего. Среднеквадратическое отклонение показывает меру отклонения наблюдений относительно среднего.

Формула расчета среднеквадратического отклонение для выборки следующая:

Разложим формулу на составные части и рассчитаем среднеквадратическое отклонение в Excel на примере нашего временного ряда.

1. Рассчитаем среднее значение для этого воспользуемся формулой Excel =СРЗНАЧ(B11:K11)

= СРЗНАЧ(ссылка на диапазон) = 100/10=10

2. Определим отклонение каждого значения ряда относительно среднего

для первой недели = 6-10=-4

для второй недели = 10-10=0

для третей = 7-1=-3 и т.д.

3. Для каждого значения ряда определим квадрат разницы отклонения значений ряда относительно среднего

для первой недели = (-4)^2=16

для второй недели = 0^2=0

для третей = (-3)^2=9 и т.д.

4. Рассчитаем сумму квадратов отклонений значений относительно среднего с помощью формулы =СУММ(ссылка на диапазон (ссылка на диапазон с )

=16+0+9+4+16+16+4+9+0+16=90

5. , для этого сумму квадратов отклонений значений относительно среднего разделим на количество значений минус единица (Сумма((Xi-Xср)^2))/(n-1)

= 90/(10-1)=10

6. Среднеквадратическое отклонение равно = корень(10)=3,2

Итак, в 6 шагов мы разложили сложную математическую формулу, надеюсь вам удалось разобраться со всеми частями формулы и вы сможете самостоятельно разобраться в других формулах.

Рассмотрим еще один показатель, который в будущем нам понадобятся – дисперсия.

Что такое среднеквадратичное отклонение

Рассматривая какие-либо величины или их изменения, используют такие критерии как среднеарифметическая величина и ее отклонение. Различные понятия позволяют оценить разброс измеряемой величины и ее отклонение. К ним относится абсолютная погрешность, которая показывает насколько каждая конкретная величина отличается от среднего значения. Но так как сумма всех абсолютных погрешностей равна нулю, то этот критерий не позволяет показать разброс измеряемых величин. И для решения этой задачи был введен новый показатель — среднее квадратичное отклонение.

Для того чтобы объяснить его смысл необходимо вспомнить некоторые основные математические понятия.

Определение

Средней величиной или средним арифметическим называется число, полученное в результате деления суммы всех величин на их количество.

Пример

Среднеарифметическое для 3 чисел b₁, b₂ и b₃ определяется как:

\(M=\frac{b_1+b_2+b_3}3\)

Со средней величиной непосредственно связана и другая характеристика — математическое ожидание.

Определение

Значение среднего арифметического некоторого множества при стремлении его членов к бесконечности называется математическим ожиданием (М).

А оценкой математического ожидания является среднее арифметическое определенного числа измерений изучаемой величины.

Определение

Вариантой или абсолютной погрешностью называется разность измеряемой величины со средним значением.

Она обозначается греческой буквой D. Для того чтобы найти варианту единичного измерения ai следует отнять от ее значение среднее арифметическое:

\(Da_i=a_i-M\)

Также для оценки единичного измерения используется и относительная погрешность, значение которой выражается в процентах. Ее вычисление проводят по формуле:

\(\sigma=\frac{\left|\triangle a_i\right|}M\times100\%\)

Относительная погрешность каждой величины позволяет отбросить из вариации измерений значения с очень большой погрешностью и проводить дальнейший анализ только величин с незначительной относительной погрешностью.

Характеристикой распределения значений некоторой измеряемой величины является дисперсия (D).

Определение

Дисперсией называется среднее арифметическое квадратов всех абсолютных погрешностей.

Теперь можно дать определение и «среднеквадратичному отклонению».

Определение

Значение корня квадратного из дисперсии случайной величины называется среднеквадратичным отклонением и обозначается «ϭ».

Оно вычисляется по формуле:

\(\sigma=\sqrt{D_{\left|x\right|}}\)

Единицей измерения среднеквадратического отклонения является единица измерения исследуемой величины. Данный критерий используется при измерении линейной функции, статической проверки гипотезы, расчете стандартной ошибки среднего арифметического, а также при построении доверительных интервалов.