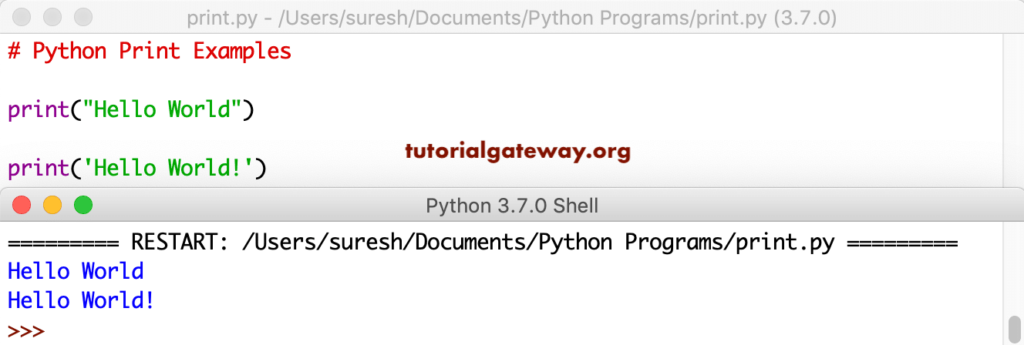
Модули

Степени, логарифмирование, экспоненцирование

math.pow(x, y)

Возвращает x в степени y.

В ситуациях или данная функция всегда возвращает \(1\) даже если x равен NaN, Inf или -Inf. Однако, если x и y являются конечными числами, причем x отрицательное, а y не целое, то будет вызвано исключение ValueError:

math.sqrt(x)

Возвращает квадратный корень числа x.

math.log(x)

Если указано только число x, то возвращается натуральный логарифм данного числа. Если указано число x и основание base, то возвращается логарифм числа по указанному основанию.

По сути, команда равносильна команде :

math.log10(x)

Возвращает десятичный логарифм числа x, вычисление которого происходит немного точнее, чем .

math.log2(x)

Возвращает двоичный логарифм числа x, вычисление которого происходит немного точнее, чем .

math.log1p(x)

Возвращает натуральный логарифм от x увеличенного на \(1\) (), значение которого расчитывается более точно, особенно для небольших чисел x.

math.exp(x)

Возвращает .

math.expm1(x)

Возвращает , которое вычисляется значительно точнее, чем , особенно для небольших чисел x.

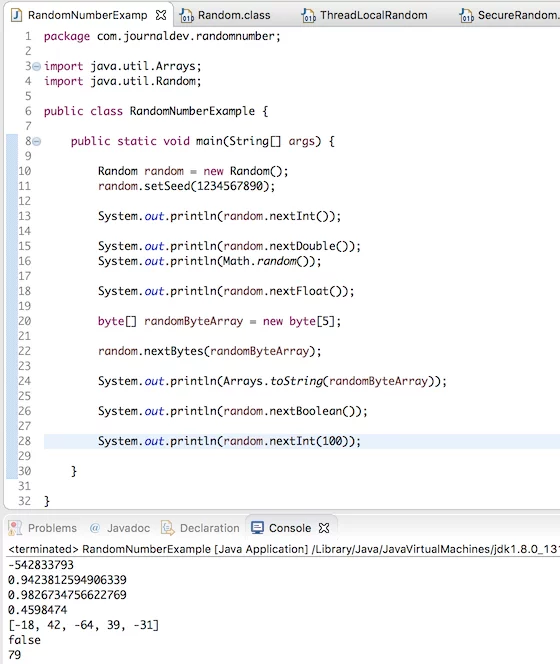
Игра в кости с использованием модуля random в Python

Далее представлен код простой игры в кости, которая поможет понять принцип работы функций модуля random. В игре два участника и два кубика.

• Участники по очереди бросают кубики, предварительно встряхнув их;
• Алгоритм высчитывает сумму значений кубиков каждого участника и добавляет полученный результат на доску с результатами;
• Участник, у которого в результате большее количество очков, выигрывает.

Код программы для игры в кости Python:

Python

import random

PlayerOne = «Анна»
PlayerTwo = «Алекс»

AnnaScore = 0
AlexScore = 0

# У каждого кубика шесть возможных значений
diceOne =
diceTwo =

def playDiceGame():
«»»Оба участника, Анна и Алекс, бросают кубик, используя метод shuffle»»»

for i in range(5):
#оба кубика встряхиваются 5 раз
random.shuffle(diceOne)
random.shuffle(diceTwo)
firstNumber = random.choice(diceOne) # использование метода choice для выбора случайного значения
SecondNumber = random.choice(diceTwo)
return firstNumber + SecondNumber

print(«Игра в кости использует модуль random\n»)

#Давайте сыграем в кости три раза
for i in range(3):
# определим, кто будет бросать кости первым
AlexTossNumber = random.randint(1, 100) # генерация случайного числа от 1 до 100, включая 100
AnnaTossNumber = random.randrange(1, 101, 1) # генерация случайного числа от 1 до 100, не включая 101

if( AlexTossNumber > AnnaTossNumber):
print(«Алекс выиграл жеребьевку.»)
AlexScore = playDiceGame()
AnnaScore = playDiceGame()
else:
print(«Анна выиграла жеребьевку.»)
AnnaScore = playDiceGame()
AlexScore = playDiceGame()

if(AlexScore > AnnaScore):
print («Алекс выиграл игру в кости. Финальный счет Алекса:», AlexScore, «Финальный счет Анны:», AnnaScore, «\n»)
else:
print(«Анна выиграла игру в кости. Финальный счет Анны:», AnnaScore, «Финальный счет Алекса:», AlexScore, «\n»)

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45

importrandom PlayerOne=»Анна» PlayerTwo=»Алекс» AnnaScore= AlexScore=   # У каждого кубика шесть возможных значений diceOne=1,2,3,4,5,6 diceTwo=1,2,3,4,5,6 defplayDiceGame() «»»Оба участника, Анна и Алекс, бросают кубик, используя метод shuffle»»» foriinrange(5) #оба кубика встряхиваются 5 раз random.shuffle(diceOne) random.shuffle(diceTwo) firstNumber=random.choice(diceOne)# использование метода choice для выбора случайного значения SecondNumber=random.choice(diceTwo) returnfirstNumber+SecondNumber print(«Игра в кости использует модуль random\n»)   #Давайте сыграем в кости три раза foriinrange(3) # определим, кто будет бросать кости первым AlexTossNumber=random.randint(1,100)# генерация случайного числа от 1 до 100, включая 100 AnnaTossNumber=random.randrange(1,101,1)# генерация случайного числа от 1 до 100, не включая 101 if(AlexTossNumber>AnnaTossNumber) print(«Алекс выиграл жеребьевку.») AlexScore=playDiceGame() AnnaScore=playDiceGame() else print(«Анна выиграла жеребьевку.») AnnaScore=playDiceGame() AlexScore=playDiceGame() if(AlexScore>AnnaScore) print(«Алекс выиграл игру в кости. Финальный счет Алекса:»,AlexScore,»Финальный счет Анны:»,AnnaScore,»\n») else print(«Анна выиграла игру в кости. Финальный счет Анны:»,AnnaScore,»Финальный счет Алекса:»,AlexScore,»\n»)

Вывод:

Shell

Игра в кости использует модуль random

Анна выиграла жеребьевку.
Анна выиграла игру в кости. Финальный счет Анны: 5 Финальный счет Алекса: 2

Анна выиграла жеребьевку.
Анна выиграла игру в кости. Финальный счет Анны: 10 Финальный счет Алекса: 2

Алекс выиграл жеребьевку.
Анна выиграла игру в кости. Финальный счет Анны: 10 Финальный счет Алекса: 8

1 2 3 4 5 6 7 8 9 10

Игравкостииспользуетмодульrandom   Аннавыигралажеребьевку. Аннавыигралаигрувкости.ФинальныйсчетАнны5ФинальныйсчетАлекса2   Аннавыигралажеребьевку. Аннавыигралаигрувкости.ФинальныйсчетАнны10ФинальныйсчетАлекса2   Алексвыигралжеребьевку. Аннавыигралаигрувкости.ФинальныйсчетАнны10ФинальныйсчетАлекса8

Вот и все. Оставить комментарии можете в секции ниже.

Звук

Благодаря нескольким очень полезным
модулям работать со звуком в Python довольно
просто.

pySonic. Python-враппер для высокопроизводительной кроссплатформенной звуковой библиотеки FMOD.

PyMedia. Модуль Python для манипуляций с файлами WAV, MP3, Ogg, AVI, DivX, DVD, CD-DA и др. Позволяет анализировать, демультиплексировать и мультиплексировать, декодировать и кодировать все поддерживаемые форматы. Может компилироваться для Windows, Linux и Cygwin.

PMIDI. Библиотека PMIDI служит оберткой для библиотеки Windows MIDI Streams, обеспечивая возможность использования последней в Python. Благодаря PMIDI разработчики могут на лету генерировать в своем коде синтезированные музыкальные последовательности, чтобы они проигрывались для пользователей.

Mutagen. Модуль для обработки метаданных аудио. Поддерживает аудиофайлы FLAC, M4A, Musepack, MP3, Ogg FLAC, Ogg Speex, Ogg Theora, Ogg Vorbis, True Audio и WavPack.

Вычисление Квадратного Корня С Помощью pow()

В этом разделе мы будем использовать встроенный метод pow() для вычисления квадратного корня в Python.

Давайте разберемся, как работает функция pow() в Python.

Метод pow() принимает 2 параметра, первый параметр-числовое значение, а второй параметр-мощность числового значения. Если мы посмотрим на него, то вы заметите, что он похож на то, как мы вычисляли квадратный корень в приведенных выше примерах.

Метод pow() принимает 2 параметра, первый параметр-числовое значение, а второй параметр-мощность числового значения. Если мы посмотрим на него, то вы заметите, что он похож на то, как мы вычисляли квадратный корень в приведенных выше примерах.

Синтаксис

pow(x,y) # где y-сила x или x**y

Пример: Вычисление квадратного корня из числа С помощью pow()

Выход:

pow() также является предопределенным методом определения мощности числа, он принимает в качестве входных данных два аргумента: первый-само число, а второй — мощность этого числа. Программа такая же, как и первая программа, где мы используем знак ( * * ), чтобы узнать квадратный корень, но единственная разница заключается в том, что здесь мы используем предопределенный метод pow() вместо знака ( * * ), чтобы получить степень этого числа.

Тригонометрические функции

Тригонометрические функции для комплексного числа также доступны в модуле .

import cmath

a = 3 + 4j

print('Sine:', cmath.sin(a))
print('Cosine:', cmath.cos(a))
print('Tangent:', cmath.tan(a))

print('ArcSin:', cmath.asin(a))
print('ArcCosine:', cmath.acos(a))
print('ArcTan:', cmath.atan(a))

Вывод:

Sine: (3.853738037919377-27.016813258003936j)
Cosine: (-27.034945603074224-3.8511533348117775j)
Tangent: (-0.0001873462046294784+0.999355987381473j)
ArcSin: (0.6339838656391766+2.305509031243477j)
ArcCosine: (0.9368124611557198-2.305509031243477j)
ArcTan: (1.4483069952314644+0.15899719167999918j)

Как отфильтровать элементы с помощью takewhile() и drop while()

Мы можем использовать Python для фильтрации элементов последовательности, если условие . Если условие становится , фильтрация прекращается.

iterator = itertools.takewhile(condition, *sequence)

Вот простой пример, который фильтрует числа, если число положительное.

import itertools

sequence = itertools.takewhile(lambda x: x > 0, )

for item in sequence:
    print(item)

Выход

1
2
3

Здесь последовательность остановилась после 3, поскольку следующий элемент равен -1.

Точно так же фильтрует элементы, пока условие имеет значение и возвращает все элементы после первого значения, отличного от false.

import itertools

data = itertools.dropwhile(lambda x: x < 5, )
for item in data:
    print(item)

Выход

12
7
1
-5

Функция exp() — вычисление экспоненты

Функция вычисляет значение экспоненты, то есть e ^ x конкретного числа переданной десятичной точки.

Синтаксис:

decimal.Decimal(decimal-number).exp()

Пример:

import decimal as d

d.getcontext().prec = 5

#Intializing with an addition operation
val = d.Decimal(12.201) + d.Decimal(12.20)

#Calculating exponential of the decimal value
exp = val.exp()

#variable with no calculations
no_math = d.Decimal(1.131231)

print("Sum: ",val)
print("Exponential: ", exp)
print(no_math)

Выход:

Decimal Number:  24.401                                                                                                       
3.9557E+10                                                                                                                    
1.131231000000000097571728474576957523822784423828125   

Следует помнить, что значение точности применяется, когда вы выполняете математические операции с двумя десятичными знаками, а не когда вы напрямую инициируете переменную со значениями, как показано с переменной «no_math» выше.

Использование itertools.tee() для клонирования последовательностей

Есть еще одна полезная функция под названием , которая клонирует последовательность и производит две последовательности.

cloned1, cloned2 = itertools.tee(original_sequence)

Это основано на команде Linux tee, которая клонирует свои выходные данные.

Здесь, когда вы клонируете последовательность с помощью , вы не можете снова использовать тот же итератор. Вы должны быть очень осторожны при использовании этой функции.

import itertools

single_iterator = itertools.islice(itertools.count(), 3)
cloned1, cloned2 = itertools.tee(single_iterator)

for num in cloned1:
    print('cloned1: {}'.format(num))
for num in cloned2:
    print('cloned2: {}'.format(num))

Выход

cloned1: 0
cloned1: 1
cloned1: 2
cloned2: 0
cloned2: 1
cloned2: 2

Действительно, мы могли видеть две клонированные последовательности с одинаковыми выходами.

Возведение в степень (**)

Нетипичный оператор для большинства других языков программирования. Тем он и удобен. Парная «звёздочка» (**) выполняет классическое математическое возведение числа «a» в степень «b»:

И показатель степени, и основание могут быть отрицательными:

И дробными:

Операндов у возведения в степень также может быть несколько. В таком случае, оператор «**» работает, как право-ассоциативный (т.е. операции выполняются справа-налево):

В завершении — про приоритет операций. Если в выражении используются разные операторы, то порядок их выполнения будет следующим:

1. возведение в степень;
2. умножение, деление, целочисленное деление и деление по модулю;
3. сложение и вычитание.

Арифметические функции в Python

Арифметические функции используются для представления чисел в различных формах и осуществления над ними математических операций. Далее представлен перечень самых популярных арифметических функций:

• : округление определенного числа вверх;
• : возвращает модуль (абсолютное значение) указанного числа;
• : округление определенного числа вниз;
• : получение наибольшего общего делителя чисел и ;
• : возвращает сумму всех элементов итерируемого объекта;
• : возвращает (e^x)-1;
• : когда значение слишком мало, вычисление может привести к значительной потери в точности. может вернуть вывод с полной точностью.

В следующем примере показано использование перечисленных выше функций:

Python

import math

num = -4.28
a = 14
b = 8

num_list =
x = 1e-4 # Малое значение x

print(‘Число:’, num)
print(‘Округление числа вниз:’, math.floor(num))
print(‘Округление числа вверх:’, math.ceil(num))
print(‘Модуль числа:’, math.fabs(num))
print(‘Наибольший общий делитель a и b: ‘ + str(math.gcd(a, b)))
print(‘Сумма элементов списка: ‘ + str(math.fsum(num_list)))
print(‘e^x (при использовании функции exp()) равно:’, math.exp(x)-1)
print(‘e^x (при использовании функции expml()) равно:’, math.expm1(x))

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17

importmath num=-4.28 a=14 b=8 num_list=10,8.25,75,7.04,-86.23,-6.43,8.4 x=1e-4# Малое значение x print(‘Число:’,num) print(‘Округление числа вниз:’,math.floor(num)) print(‘Округление числа вверх:’,math.ceil(num)) print(‘Модуль числа:’,math.fabs(num)) print(‘Наибольший общий делитель a и b: ‘+str(math.gcd(a,b))) print(‘Сумма элементов списка: ‘+str(math.fsum(num_list))) print(‘e^x (при использовании функции exp()) равно:’,math.exp(x)-1) print(‘e^x (при использовании функции expml()) равно:’,math.expm1(x))

Вывод

Python

Число: -4.28
Округление числа вниз: -5
Округление числа вверх: -4
Модуль числа: 4.28
Наибольший общий делитель a и b: 2
Сумма элементов списка: 16.029999999999998
e^x (при использовании функции exp()) равно: 0.0001000050001667141
e^x (при использовании функции expml()) равно: 0.00010000500016667084

1 2 3 4 5 6 7 8

Число-4.28 Округлениечиславниз-5 Округлениечиславверх-4 Модульчисла4.28 Наибольшийобщийделительaиb2 Суммаэлементовсписка16.029999999999998 e^x(прииспользованиифункцииexp())равно0.0001000050001667141 e^x(прииспользованиифункцииexpml())равно0.00010000500016667084

К числу других математических функций относятся:

• : принимает два вещественных аргумента, возводит первый аргумент в степень, значением которой является второй аргумент, после чего возвращает результат. К примеру, эквивалентно выражению ;
• : возвращает квадратный корень определенного числа.

Примеры данных методов представлены ниже:

Возведение в степень

Python

math.pow(3, 4)

1	math.pow(3,4)

Вывод

Shell

81.0

1

81.0

Квадратный корень

Python

math.sqrt(81)

1	math.sqrt(81)

Вывод

Shell

9.0

1

9.0

Число Пи из библиотеки math

Первой важной математической константой является число Пи (π). Оно обозначает отношение длины окружности к диаметру, его значение 3,141592653589793

Чтобы получить к нему доступ, сначала импортируем библиотеку math следующим образом:

Python

import math

1	importmath

Затем можно получить доступ к константе, вызывая :

Python

math.pi

1

math.pi

Вывод

Shell

3.141592653589793

1	3.141592653589793

Данную константу можно использовать для вычисления площади или длины окружности. Далее представлен пример простого кода, с помощью которого это можно сделать:

Python

import math

radius = 2
print(‘Площадь окружности с радиусом 2 равна:’, math.pi * (radius ** 2))

1 2 3 4

importmath radius=2 print(‘Площадь окружности с радиусом 2 равна:’,math.pi*(radius**2))

Вывод

Shell

Площадь окружности с радиусом 2 равна: 12.566370614359172

1	Площадьокружностисрадиусом2равна12.566370614359172

Мы возвели радиус во вторую степень и умножили значение на число Пи, как и следовало сделать в соответствии с формулой πr2.

Функция sqrt() — квадратный корень

Функция sqrt() вычисляет и возвращает значение квадратного корня из переданного десятичного числа.

Синтаксис:

decimal.Decimal(decimal-number).sqrt()

Пример:

import decimal as d

d.getcontext().prec = 3

val = d.Decimal(122.20)
sqrt = val.sqrt()
print("Decimal Number: ",val)
print("Square root of the decimal number: ",sqrt)

Выход:

Decimal Number:  122.2000000000000028421709430404007434844970703125
Square root of the decimal number:  11.1

Снова обратите внимание, как объявленное значение содержит полное десятичное число, в то время как вычисленное значение соответствует нашему набору точности из 3 цифр

Для генерации последовательности на основе счетчика

Мы можем использовать функцию Python чтобы сделать итераторы соответствующими .

iterator = itertools.count(start=0, step=1)

Здесь это итератор, который ведет счет бесконечно, начиная с 0 и далее. Продолжает увеличивать счет на . Мы также можем установить десятичное или отрицательное число.

Например, если вы хотите доказать, что у вас бесконечный цикл, вы можете запустить приведенный ниже фрагмент, но это НЕ рекомендуется.

Просто убедитесь, что считается бесконечно.

for num in itertools.count(start=0, step=1):
    # Infinite loop!
    print(num)

Использование этой функции может не сразу показаться вам очевидным, вы можете комбинировать ее с другими функциями, такими как метод zip, для создания последовательностей.

Рассмотрим пример ниже:

import itertools
numbers = 

data = list(zip(itertools.count(0, 10), numbers))

print(data)

Здесь вы можете увидеть мощь итераторов. Поскольку итераторы производят выходные данные только по запросу, мы можем использовать с другой конечной итерацией, например списком.

Теперь это используется для создания индексов для элементов в списке.

Теперь, если вы хотите иметь подмножество последовательности итератора с помощью Python , вы также можете использовать для создания только части итератора.

import itertools

for num in itertools.islice(itertools.count(start=0, step=10), 4):
    print(num)

for num in itertools.islice(itertools.count(), 0, 50, 10):
    print(num)

Выход

0
10
20
30
0
10
20
30
40

Как видите, обе последовательности идентичны. Это показывает, что у вас может быть несколько подходов к созданию последовательностей.

Графический интерфейс

В стандартной библиотеке Python есть
графическая библиотека интерфейсов
Tkinter. Но при помощи внешних модулей вы
можете поднять GUI ваших приложений на
новый уровень.

wxPython. Создает по-настоящему нативные пользовательские интерфейсы для Python-приложений, которые могут запускаться на Windows, Mac и Linux, а также прочих Unix-подобных системах практически без каких-либо модификаций.

PyGObject. Пакет Python, предоставляющий привязки для библиотек на базе Gobject, таких как GTK, GStreamer, WebKitGTK, GLib, GIO и др.

Pmw. Набор инструментов для создания на Python высокоуровневых составных виджетов (с использованием модуля Tkinter).

WCK. Расширение API, позволяющее реализовывать на чистом Python всевозможные пользовательские виджеты.

Tix. Мощный набор компонентов пользовательского интерфейса, при помощи которого можно расширить возможности ваших Tcl/Tk и Python-приложений. Использование Tix вместе с Tk очень улучшает внешний вид и функционал приложений.

3 Логарифмические функции

Модуль предоставляет нам следующие функции для вычисления логарифмических значений чисел с десятичной запятой:

• decimal.ln();
• decimal.log10().

Функция возвращает значение натурального десятичного числа, как показано ниже.

decimal.Decimal(decimal-number).ln()

Функция decimal.log10() используется для вычисления значения журнала по основанию 10 переданного ей десятичного числа.

decimal.Decimal(decimal-number).log10()

Пример:

import decimal as d

d.getcontext().prec = 2

val = d.Decimal(122.20)

log = val.ln()
print("Natural log value of the decimal number: ",log)

log_10 = val.log10()
print("Log value with base 10 of the decimal number: ",log_10)

Выход:

Natural log value of the decimal number:  4.8
Log value with base 10 of the decimal number:  2.1

Целое число

Целые числа — это целые числа. Они могут быть положительными или отрицательными. Они должны быть без десятичных значений.

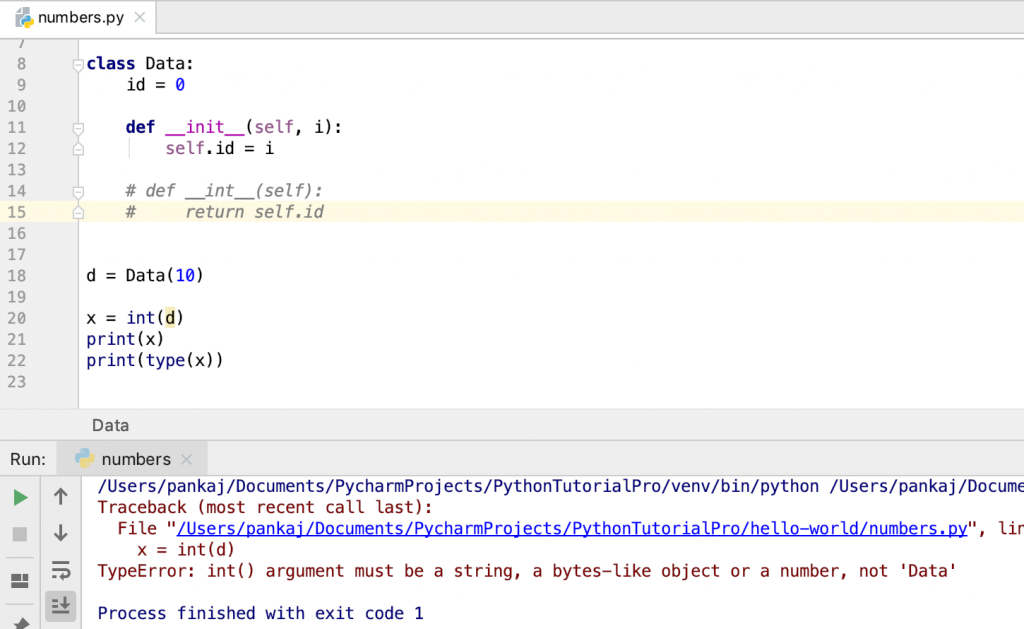
Мы можем использовать функцию int(), чтобы получить целочисленное представление объекта. В объекте должен быть реализован метод __int __(), который возвращает целое число.

Давайте рассмотрим несколько примеров.

x = 10
print(type(x))

x = int("10")
print(type(x))


class Data:
    id = 0

    def __init__(self, i):
        self.id = i

    def __int__(self):
        return self.id


d = Data(10)

x = int(d)
print(x)
print(type(x))

Вывод:

<class 'int'>
<class 'int'>
10
<class 'int'>

Класс String предоставляет метод __int __(), поэтому мы можем легко преобразовать строку в int с помощью метода int().

Если объект не реализует метод __int __(), функция int() выдает ошибку TypeError.

Обычно целые числа определяются на основе 10. Но мы также можем определять их в двоичном, восьмеричном и шестнадцатеричном формате.

i = 0b1010
print(i)  # 10

i = 0xFF
print(i)  # 255

i = 0o153
print(i)  # 107

Разработка игр

Python — это очень разносторонний язык,
позволяющий программистам создавать
самые разнообразные приложения, включая
видеоигры.

Pygame. Набор модулей для написания видеоигр. Pygame расширяет функционал прекрасной библиотеки SDL. Благодаря ему на Python можно создавать полнофункциональные игры и мультимедиа-программы.

Pyglet. Мощная, но при этом простая в использовании библиотека Python для разработки игр и других приложений с большим количеством визуальных эффектов для Windows, Mac OS X и Linux.

pyOpenGL. Этот модуль чаще других используется для обеспечения работы с библиотекой OpenGL и связанными с нею API в программах на Python.

Приоритеты операторов

Consider this expression:

>>> 20 + 4 * 10
60

There is ambiguity here. Should Python perform the addition first and then multiply the sum by ? Or should the multiplication be performed first, and the addition of second?

Clearly, since the result is , Python has chosen the latter; if it had chosen the former, the result would be . This is standard algebraic procedure, found universally in virtually all programming languages.

Всем операторам, которые поддерживает язык, присваивается приоритет. В выражении все операторы с наивысшим приоритетом выполняются первыми. Как только эти результаты получены, выполняются операторы следующего наивысшего приоритета. Так продолжается до тех пор, пока выражение не будет полностью оценено. Все операторы с одинаковым приоритетом выполняются в порядке слева направо.

Вот порядок приоритета операторов Python, которые вы видели до сих пор, от низшего к высшему:

 
Оператор
Описание

низший приоритет

Логическое ИЛИ

Логическое И

Логическое НЕ

, , , , , , ,

сравнения, идентификация

побитовое ИЛИ

побитовое ИСКЛЮЧАЮЩЕЕ ИЛИ

побитовое И

,

битовый сдвиг

,

сложение, вычитание

, , ,

умножение, деление, окруляющее деление, остаток от деления

, ,

плюс, минус, побитовый минус

наивысший приоритет

возведение в степень

 
Операторы в верхней части таблицы имеют самый низкий приоритет, а операторы в нижней части таблицы имеют самый высокий. Любые операторы в одной строке таблицы имеют одинаковый приоритет.

Понятно, почему умножение выполняется первым в приведенном выше примере: умножение имеет более высокий приоритет, чем сложение.

Аналогично, в приведенном ниже примере сначала возводится в степень , что равно , а затем выполняется умножение в порядок слева направо():

>>> 2 * 3 ** 4 * 5
810

Приоритеты операторов могут быть переопределены с помощью скобок. Выражения в скобках всегда выполняются в первую очередь, перед выражениями, которые не заключены в скобки. Таким образом, происходит следующее:

>>> 20 + 4 * 10
60
>>>(20 + 4) * 10
240

>>> 2 * 3 ** 4 * 5
810
>>> 2 * 3 **(4 * 5)
6973568802

В первом примере сначала вычисляется , затем результат умножается на . Во втором примере сначала вычисляется , затем значение увеличивается до этой степени, а затем результат умножается на .

Нет ничего плохого в том, чтобы свободно использовать круглые скобки, даже если они не нужны для изменения порядка оценки. Фактически, это считается хорошей практикой, потому что это может сделать код более читабельным, и это освобождает читателя от необходимости вызывать Приоритеты операторов из памяти. Учтите следующее:

(a < 10) and(b > 30)

Здесь круглые скобки совершенно не нужны, поскольку операторы сравнения имеют более высокий приоритет, чем , и в любом случае выполнялись бы первыми. Но некоторые могут считать намерение версии в скобках более очевидным, чем эта версия без скобок:

a < 10 and b > 30

С другой стороны, вероятно, есть те, кто предпочел бы последнее; это вопрос личных предпочтений. Дело в том, что вы всегда можете использовать круглые скобки, если считаете, что это делает код более читабельным, даже если в них нет необходимости менять порядок вычислений.

Создать комбинации с помощью combinations()

Мы также можем создавать последовательности комбинаций, используя Python .

iterator = itertools.combinations(*sequence, r)

Вот простой пример:

import itertools
words = 
results = itertools.combinations(words, 2)
for item in results:
    print(item)

Выход

('hello', 'from')
('hello', 'AskPython')
('hello', 'how')
('from', 'AskPython')
('from', 'how')
('AskPython', 'how')

Если вы хотите, чтобы в комбинациях повторялись последовательные элементы, вы можете использовать .

results = itertools.combinations_with_replacement(words, 3)

for item in results:
    print(item)

Выход

('hello', 'hello', 'hello')
('hello', 'hello', 'from')
('hello', 'hello', 'AskPython')
('hello', 'hello', 'how')
('hello', 'from', 'from')
('hello', 'from', 'AskPython')
('hello', 'from', 'how')
('hello', 'AskPython', 'AskPython')
('hello', 'AskPython', 'how')
('hello', 'how', 'how')
('from', 'from', 'from')
('from', 'from', 'AskPython')
('from', 'from', 'how')
('from', 'AskPython', 'AskPython')
('from', 'AskPython', 'how')
('from', 'how', 'how')
('AskPython', 'AskPython', 'AskPython')
('AskPython', 'AskPython', 'how')
('AskPython', 'how', 'how')
('how', 'how', 'how')

Точно так же вы можете перечислить перестановки, используя и .