Установка и первое знакомство

Numpy Mode

One thing which should be noted is that there is no in-built function for finding mode using any numpy function. For this, we will use scipy library. First we will create numpy array and then we’ll execute the scipy function over the array.

Syntax

Now we will go over scipy mode function syntax and understand how it operates over a numpy array.

scipy.stats.mode(a, axis=0, nan_policy=’propagate’)

a : array-like – This consists of n-dimensional array of which we have to find mode(s).

axis – int or None (optional) – This is the axis along which to operate. Default is 0. If None, computing mode over the whole array a

nan_policy – {‘propagate’, ‘raise’, ‘omit’} (optional) – This defines how to handle when input contains nan. The following options are available default is propagate which returns nan, raise throws an error and omit performs the calculations ignoring nan values.

As output, two different types of values are produced. First is the mode which is of ndarray type and it consists of array of modal values. The second is count which is again of ndarray type consisting of array of counts for each mode.

Операции со срезами matrix в Python

Часто мы работаем не с целым массивом, а с его компонентами. Эти операции выполняются с помощью метода слайс (срез). Он пришел на замену циклу for, при котором каждый элемент подвергался перебору. Метод позволяет получать копии matrix, причём манипуляции выполняются в виде . В данном случае start — индекс элемента, с которого берётся отсчёт, stop — последний элемент, step — размер шага или число пропускаемых значений элемента при каждой итерации. Изначально start равен нулю, stop — индексу последнего элемента, step — единице. Если выполнить операции без аргументов, копирование и добавление списка произойдёт полностью.

Допустим, имеем целочисленный массив otus = . Для копирования и вывода используем otus. В итоге произойдёт вывод последовательности . Но если аргументом станет отрицательное значение, допустим, -2, произойдёт вывод уже других данных:

otus-2]; //4 

Возможны и другие операции. Например, если добавить ещё одно двоеточие, будет указан шаг копируемых элементов. Таким образом, otus позволит вывести матрицу .

Если ввести отрицательное значение, к примеру, отсчёт начнётся с конца, и в результате произойдёт вывод . Остаётся добавить, что метод среза позволяет гибко работать с матрицами и вложенными списками в Python.

Хотите узнать гораздо больше? Записывайтесь на курс «Разработчик Python»!

1.2. Заполнение данными

Создает массив NumPy.

Преобразует последовательность в массив NumPy.

Преобразует последовательность в массив NumPy, пропуская подклассы ndarray.

Возвращает непрерывный массив в памяти с организацией порядка элементов в С-стиле.

Интерпретирует входные данные как матрицу.

Возвращает копию массива.

Преобразует буфер в одномерный массив.

Создает массив из текстового или двоичного файла.

Создает массив с выполнением указанной функции над каждым элементом.

Создает одномерный массив из итерируемого объекта.

Создает одномерный массив из строки.

Создает массив из данных в текстовом файле.

Разделение матрицы

Разделение одномерного массива NumPy аналогично разделению списка. Рассмотрим пример:

import numpy as np
letters = np.array()

# с 3-го по 5-ый элементы
print(letters)        # Вывод: 

# с 1-го по 4-ый элементы
print(letters)        # Вывод:    

# с 6-го до последнего элемента
print(letters)         # Вывод:

# с 1-го до последнего элемента
print(letters)          # Вывод:

# список в обратном порядке
print(letters)          # Вывод:

Теперь посмотрим, как разделить матрицу.

import numpy as np

A = np.array(, 
    ,
    ])

print(A)  # две строки, четыре столбца

''' Вывод:

 ]
'''


print(A)  # первая строка, все столбцы

''' Вывод:
` 1  4  5 12 14`
'''

print(A)  # все строки, второй столбец

''' Вывод:

'''

print(A)  # все строки, с третьего по пятый столбец
''' Вывод:

 
 ]
'''

Использование NumPy вместо вложенных списков значительно упрощает работу с матрицами. Мы рекомендуем детально изучить пакет NumPy, если вы планируете использовать Python для анализа данных.

Данная публикация является переводом статьи «Python Matrices and NumPy Arrays» , подготовленная редакцией проекта.

Операции с матрицами

Выше мы привели пример сложение, умножение матриц и транспонирование матрицы. Мы использовали вложенные списки, прежде чем создавать эти программы. Рассмотрим, как выполнить ту же задачу, используя массив NumPy.

Сложение двух матриц или сумма элементов массива Python

Мы используем оператор +, чтобы сложить соответствующие элементы двух матриц NumPy.

import numpy as np

A = np.array(, ])
B = np.array(, ])
C = A + B      # сложение соответствующих элементов
print(C)

''' 
Вывод:

 ]
 '''

Умножение двух матриц Python

Чтобы умножить две матрицы, мы используем метод dot(). Узнайте больше о том, как работает numpy.dot .

Примечание: * используется для умножения массива (умножения соответствующих элементов двух массивов), а не умножения матрицы.

import numpy as np

A = np.array(, ])
B = np.array(, , ])
C = a.dot(B)
print(C)

''' 
Вывод:

 ]
'''

Транспонирование матрицы питон

Мы используем numpy.transpose для вычисления транспонирования матрицы.

import numpy as np

A = np.array(, , ])
print(A.transpose())

''' 
Вывод:

 ]
'''

Как видите, NumPy значительно упростил нашу задачу.

slicing:

As you can see the ‘reshape’ function has shown its magic. Now, let’s take another operation i.e Slicing. Slicing is basically extracting a particular set of elements from an array. This slicing operation is pretty much similar to the one which is there in the list as well. Consider the example on the left side:

Before getting into the above example, let’s see a simple one. We have an array and we need a particular element (say 3) out of a given array. Let’s consider the below example:

import numpy as npa=np.array()print(a)Output - 3

Here, the array(1,2,3,4) is your index 0 and (3,4,5,6) is index 1 of the python numpy array. Therefore, we have printed the second element from the zeroth index. Taking one step forward, let’s say we need the 2nd element from the zeroth and first index of the array. Let’s see how you can perform this operation:

import numpy as npa=np.array()print(a)Output - 

Here colon represents all the rows, including zero. Now to get the 2nd element, we’ll call index 2 from both of the rows which gives us the value 3 and 5 respectively.

Next, just to remove the confusion, let’s say we have one more row and we don’t want to get its 2nd element printed just like the image above. What we can do in such a case? Consider the below code:

import numpy as npa=np.array()print(a)Output - 

As you can see in the above code, only 9 and 11 gets printed. Now when I have written 0:2, this does not include the second index of the third row of an array. Therefore, only 9 and 11 gets printed else you will get all the elements i.e .

Add array element

You can add a NumPy array element by using the append() method of the NumPy module.

The syntax of append is as follows:

numpy.append(array, value, axis)

The values will be appended at the end of the array and a new ndarray will be returned with new and old values as shown above.

The axis is an optional integer along which define how the array is going to be displayed. If the axis is not specified, the array structure will be flattened as you will see later.

Consider the following example where an array is declared first and then we used the append method to add more values to the array:

import numpy

a = numpy.array()

newArray = numpy.append (a, )

print(newArray)

The output will be like the following:

1.1. Автозаполнение массивов

Возвращает новый массив заданной формы и типа без инициированных записей.

Возвращает новый массив с формой и типом данных указанного массива без инициированных записей.

Возвращает новый массив в котором диагональные элементы равны единице, а все остальные равны нулю.

Возвращает новый квадратный массив с единицами по главной диагонали.

Возвращает новый массив заданной формы и типа, заполненный единицами.

Возвращает новый массив с формой и типом данных указанного массива, заполненный единицами.

Возвращает новый массив заданной формы и типа, заполненный нулями.

Возвращает новый массив с формой и типом данных указанного массива, заполненный нулями.

Возвращает новый массив заданной формы и типа все элементы которого равны указанному значению.

Возвращает новый массив с формой и типом данных указанного массива, все элементы которого равны указанному значению.

Основы индексирования и срезы

Существует много способов выбора подмножества данных или элементов
массива. Одномерные массивы — это просто, на первый взгляд они
аналогичны спискам Python:

In : arr = np.arange(10)

In : arr
Out: array()

In : arr
Out: 5

In : arr
Out: array()

In : arr = 12

In : arr
Out: array()

Как видно, если присвоить скалярное значение срезу, как например,
, значение присваивается всем элементам среза. Первым
важным отличием от списков Python заключается в том, что срезы массива
являются представлениями исходного массива. Это означает, что данные
не копируются и любые изменения в представлении будут отражены в
исходном массиве.

Рассмотрим пример. Сначала создадим срез массива :

In : arr_slice = arr

In : arr_slice
Out: array()

Теперь, если мы изменим значения в массиве , то они
отразятся в исходном массиве :

In : arr_slice = 12345

In : arr
Out: 
array()

«Голый» срез присвоит все значения в массиве:

In : arr_slice = 64

In : arr
Out: array()

Поскольку NumPy был разработан для работы с очень большими массивами,
вы можете представить себе проблемы с производительностью и памятью,
если NumPy будет настаивать на постоянном копировании данных.

Замечание

Если вы захотите скопировать срез в массив вместо отображения, нужно
явно скопировать массив, например, .

С массивами более высокой размерности существует больше вариантов. В
двумерных массивах каждый элемент это уже не скаляр, а одномерный
массив.

In : arr2d = np.array(, , ])

In : arr2d
Out: array()

Таким образом, к отдельному элементу можно получить доступ
рекурсивно, либо передать разделенный запятыми список
индексов. Например, следующие два примера эквивалентны:

In : arr2d
Out: array()

In : arr2d[]
Out: 3

Если в многомерном массиве опустить последние индексы, то возвращаемый
объект будет массивом меньшей размерности. Например, создадим массив
размерности \( 2 \times 2 \times 3 \):

In : arr3d = np.array(, ], , ]])

In : arr3d
Out: 
array(,
        ],

       ,
        ]])

При этом — массив размерности \( 2 \times 3 \):

In : arr3d[]
Out: 
array(,
       ])

Можно присваивать как скаляр, так и массивы:

In : old_values = arr3d[].copy()

In : arr3d[] = 42

In : arr3d
Out: 
array(,
        ],

       ,
        ]])

In : arr3d[] = old_values

In : arr3d
Out: 
array(,
        ],

       ,
        ]])

Аналогично, возвращает все значения, чьи индексы
начинаются с , формируя одномерный массив:

In : arr3d
Out: array()

Это выражение такое же, как если бы мы проиндексировали в два этапа:

In : x = arr3d

In : x
Out: 
array(,
       ])

In : x[]
Out: array()

Индексирование с помощью срезов

Как одномерные объекты, такие как списки, можно получать срезы
массивов посредством знакомого синтаксиса:

In : arr
Out: array()

In : arr
Out: array()

Рассмотрим введенный выше двумерный массив . Получение срезов
этого массива немного отличается от одномерного:

In : arr2d
Out: 
array(,
       ,
       ])

In : arr2d
Out: 
array(,
       ])

Как видно, мы получили срез вдоль оси 0, первой оси. Срез, таким
образом, выбирает диапазон элементов вдоль оси. Выражение
можно прочитать как «выбираем первые две строки массива ».

Можно передавать несколько срезов:

In : arr2d
Out: 
array(,
       ])

При получении срезов мы получаем только отображения массивов того же
числа размерностей. Используя целые индексы и срезы, можно получить
срезы меньшей размерности:

In : arr2d
Out: array()

In : arr2d
Out: array()

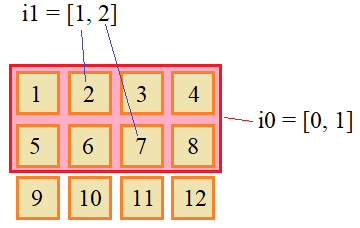
Смотрите рис. .

Рисунок 1: Срезы двумерного массива

Фундаментальный элемент NumPy – массив (array)

Отлично,
сложнейший этап установки и импорта пакета позади. Пришло время сделать первые
шаги и вначале познакомиться с его фундаментальным элементом – однородным
многомерным массивом. В NumPy элементы массива имеют единый тип
данных. Их индексы описываются кортежем целых неотрицательных чисел.
Размерность кортежа – это ранг массива (то есть, размерность массива), а каждое
число в кортеже представляет свою отдельную ось:

Как создать
массив в NumPy? Существует много
способов, но базовый реализуется через функцию:

numpy.array(object,
dtype=None, …)

Здесь в качестве
первого параметра object может выступать список или кортеж, а также функция или объект, возвращающий список или
кортеж. Второй параметр dtype – это тип элементов массива. Если
указано значение None, то тип будет определяться автоматически на основе
переданных данных. Подробнее об этой функции можно, как всегда, почитать на
странице официальной документации:

Итак, в самом
простом варианте можно создать одномерный массив так:

a = np.array(1, 2, 3, 4)

В результате
получим объект типа array с элементами 1, 2, 3, 4:

array()

Какой будет тип
у этих элементов? Мы можем его посмотреть с помощью атрибута dtype, выполнив в
консоли строчку:

a.dtype

Увидим:

dtype(‘int32’)

То есть,
автоматически был применен целочисленный тип размерностью 32 бит. Ну, хорошо, а
что если попробовать создать массив с разными типами его элементов, например,
так:

a = np.array(1, 2, "3", True)

В результате
увидим, следующее содержимое:

array(, dtype='<U11′)

Все элементы
стали строкового типа. Этот пример показывает, что в массивах NumPy используется
единый тип данных его элементов: или все целочисленные, или строковые, или
вещественные и так далее. Смешение типов в рамках одного массива не
допускается.

Отлично, это мы
сделали. Как теперь можно обращаться к отдельным элементам массива? Для этого
используется общий синтаксис:

<имя массива>

Например, для
нашего одномерного случая, мы можем взять первый элемент из массива a, следующим
образом:

a

Увидим значение ‘1’.
Обратите внимание, первый элемент имеет индекс 0, а не 1. Единица – это уже
второй элемент:

a1 # возвращает 2-й элемент со значением ‘2’

Для изменения
значения элемента, достаточно присвоить ему новое значение, например:

a1 = '123'

в результате
получим массив:

array(, dtype='<U11′)

А что будет,
если мы попробуем присвоить значение другого типа данных, например, число:

a1 = 234

Ошибки не будет,
а значение автоматически будет преобразовано в строку:

array(, dtype='<U11′)

Разработчики
пакета NumPy постарались
сделать его максимально дружественным, чтобы инженер сосредотачивался именно на
решении задачи, а не на нюансах программирования. Поэтому везде, там где это
допустимо, пакет NumPy берет на себя разрешение подобных
нюансов. И, как показала практика, это очень удобно и заметно облегчает жизнь
нам, простым смертным.

Creating Python ndarray

The Python Numpy module has a ndarray object, shorter version of N-dimensional array, or an array. Like any other programming language array, this Numpy ndarray object allows you to store multiple items of the same data type.

The following are the list of available functions to create an Array by the Python Numpy module.

• array function: which helps you to create an array or convert the data from List, Tuple, or any sequence of items (something like range) to ndarray.
• asarray function: Use this to convert the input data to Python ndarray. However, it won’t copy if the given input is already a ndarray.
• zeros: Creates an array of 0’s of specified shape and type.
• zeros_like: Same as zeros. However, it takes another array to get shape and dtype.
• ones: Creates an array of 1’s of a given shape and data type.
• ones_like: It accepts another array to read its shape and data type.
• empty, empty_like: These functions create an empty array by allocating some memory to them.
• arange: This creates or returns an array of elements in a given range. Same as range function.
• eye, identity: creates a square identity matrix in Python.

Create an Array in Python using the array function

As we said earlier, array function converts the given list, tuple, or any sequence for that matter into an array. It is a simple example to create an array in Python.

Create an Array from List in Python

Here, we declared an integer list of numbers from 1 to 5. Next, we used the array function available in the numpy module to convert that list into an array.

Let me create an ndarray of mixed items in Python.

Let me create a Python Numpy ndarray from a list of lists. Here, we declared a nested list of lists with integer values. Next, we used the array function to convert the list to Numpy array.

You might wonder, why don’t we use Lists when it looks like the same?. Arrays meant to perform vectorized operations. I mean, when you perform any operation or use any function, then that function applied to each item in an array.

We show those operations in the upcoming topic. However, we use a simple example to show you the same.

You can also create an array from a Tuple in Python.

Placing or Nesting two lists inside a [] brackets create a two-dimensional array.

Here, we are creating a 3 * 3 matrix or three-dimensional array.

Create an Array using srange

In this example, we are using the Python Numpy arange function to create an array of numbers range from 0 to n-1, where n is the given number. For example, np.arange(5) retunes an array of numbers in sequence from 0 to 4.

Create an Array using linspace in Python

In this example, we used the Python Numpy linspace function. The syntax behind this function is:

Here, we created three arrays of numbers range from 0 to n serrated by steps. For example, np.linspace(0, 1, 5) retunes an array of numbers from 0 to 1 in five equal steps.

Apart from an array function, the NumPy module has few other functions to create an ndarray. They are zeros, ones, and empty functions.

Python zeros array

The Python zeros function creates an array of zeros. This function accepts the arguments to specify the shape of an array. For example,

• zeros(2) means a one-dimensional array of two zero elements.
• zeros(2, 3) means 2 * 3 matrix of zeros.
• and zeros(2, 3, 4) means a three-dimensional array of zeros.

Python ones array

The Python ones function to create an array of 1’s. This numpy ones function accepts the arguments to specify the shape or number of items of an array. For example,

• ones(4) means a one-dimensional array of four 1’s.
• ones(2, 4) means 2 * 4 matrix of ones and ones(2, 3, 4) means 3D array 2 * 3 * 4 of 1’s.

Use the Python NumPy random function to create an array of random numbers. Please visit Python Random Array article

Python empty array

The Python empty function creates an empty array. It is not always an empty array, and it might load garbage values or zeros, etc. So, don’t be surprised!.

The NumPy full function creates an array of a given number.

The Python eye function creates an identical N * N matrix, where N is the given argument value.

Numpy Mean : np.mean()

The numpy mean function is used for computing the arithmetic mean of the input values. Arithmetic mean is the sum of the elements along the axis divided by the number of elements.

We will now look at the syntax of numpy.mean() or np.mean().

Ad

Syntax

numpy.mean(a, axis=some_value, dtype=some_value, out=some_value, keepdims=some_value)

a : array-like – Array containing numbers whose mean is desired. If a is not an array, a conversion is attempted.

axis : None or int or tuple of ints (optional) – This consits of axis or axes along which the means are computed.

dtype : data-type (optional) – It is the type used in computing the mean. For integer inputs, the default is float64; for floating point inputs, it is the same as the input dtype.

out : ndarray (optional) – This is the alternate output array in which to place the result. The default is None; if provided, it must have the same shape as the expected output

keepdims : bool (optional) – If this is set to True, the axes which are reduced are left in the result as dimensions with size one. With this option, the result will broadcast correctly against the input array. If the default value is passed, then keepdims will not be passed through to the mean method of sub-classes of ndarray

The output of numpy mean function is also an array, if out=None then a new array is returned containing the mean values, otherwise a reference to the output array is returned.

dtype:

You can find the data type of the elements that are stored in an array. So, if you want to know the data type of a particular element, you can use ‘dtype’ function which will print the datatype along with the size. In the below code, I have defined an array where I have used the same function.

import numpy as npa = np.array()print(a.dtype)Output - int32

As you can see, the data type of the array is integer 32 bits. Similarly, you can find the size and shape of the array using ‘size’ and ‘shape’ function respectively.

import numpy as npa = np.array()print(a.size)print(a.shape)Output - 6 (1,6)

Next, let us move forward and see what are the other operations that you can perform with python numpy module. We can also perform reshape as well as slicing operation using python numpy operation. But, what exactly is reshape and slicing? So let me explain this one by one in this python numpy tutorial.

Python Array Functions

Python NumPy has many built-in functions. We already explained all these functions with examples on regular Python Tutorial.

Python Numpy Array functions and operators	List of Numpy Functions and Operators
Arithmetic Operators	+, -, *, /
Arithmetic Functions	add, subtract, multiply, divide, mod, remainder
Aggregate Functions	sum, average, prod, min, max, maximum, minimum, mean, median, var, std, cumsum, cumprod, percentile, argmin, argmax, corrcoef
Bitwise Operators	&, |, ~, ^, left_shift, right_shift
Bitwise Functions	bitwise_and, bitwise_or, bitwise_not, bitwise_xor
Comparison Operators	<, <=, ==, <, >=, !=
Comparison Functions	equal, less, less_equal, greater, greater_equal, not_equal
Logical Operators	and, or, not
Logical Functions	logical_and, logical_or, logical_not, logical_xor
Exponential	exp, exp2, expm1, log, log2, log10, log1p
Mathematical	abs, ceil, floor, mod, modf, round, sinc, sign, trunc, square, reciprocal, power, sqrt, cbrt
Trigonometric	sin, cos, tan, acsin, arccos, atctan, arctan2, radians, degrees, hypot, deg2rad, rad2deg, unwrap
Hyperbolic	sinh, acsinh, cosh, arccosh, tanh, atctanh
Predicates	isfinite, isinf, isnan, signbit

Разделение массивов

Массивы в NumPy можно не только
объединять, но и разделять. Для этого существуют специальные функции hsplit и
vsplit. Рассмотрим их работу на простых примерах. Пусть имеется одномерный
массив из 10 элементов:

a = np.arange(10)

И мы хотим
разделить его на две равные части. Это реализуется с помощью функции hsplit:

np.hsplit(a, 2)

которая
возвращает список из двух массивов. Второй параметр 2 указывает число частей,
на которые делится исходный массив. Причем, деление выполняется по горизонтали.
Если в нашем примере указать 3 части, то возникнет ошибка:

np.hsplit(a, 3) # ошибка 10 на 3 нацело не делится

так как 10
элементов нельзя равномерно разбить на 3 части.

Также ошибка
будет и при разбиении этого массива по вертикали:

np.vsplit(a, 2) # ошибка: нет вертикальной оси

так как массив
имеет одну горизонтальную ось. Чтобы вторая функция сработала, преобразуем
массив a в вектор
столбец:

a.shape = 10, -1 # вектор-столбец

а, затем,
разобьем по вертикали:

np.vsplit(a, 2)

На выходе
получим два одномерных массива длиной 5 элементов.

Эти же функции
можно использовать и с многомерными массивами, например, так:

a = np.arange(12)
a.resize(2, 6) # двумерный массив 2x6
 
np.hsplit(a, 2) # разбиение по горизонтали
np.vsplit(a, 2) # разбиение по вертикали

Функция array_split

Рассмотренные
функции выполняют разбиение или по первой оси axis0 или по второй
оси axis1. Но что если
нам нужно выполнить разбиение по произвольной оси многомерного массива? Для
этого существует функция array_split(). Ее работа аналогична рассмотренным выше
функциям, только дополнительно указывается ось разбиения. Например:

a = np.arange(18)
a.resize(3, 3, 2)
 
np.array_split(a, 2, axis=2)
np.array_split(a, 3, axis=)
np.array_split(a, 3, axis=1)

Видео по теме

#1. Пакет numpy — установка и первое знакомство | NumPy уроки

#2. Основные типы данных. Создание массивов функцией array() | NumPy уроки

#3. Функции автозаполнения, создания матриц и числовых диапазонов | NumPy уроки

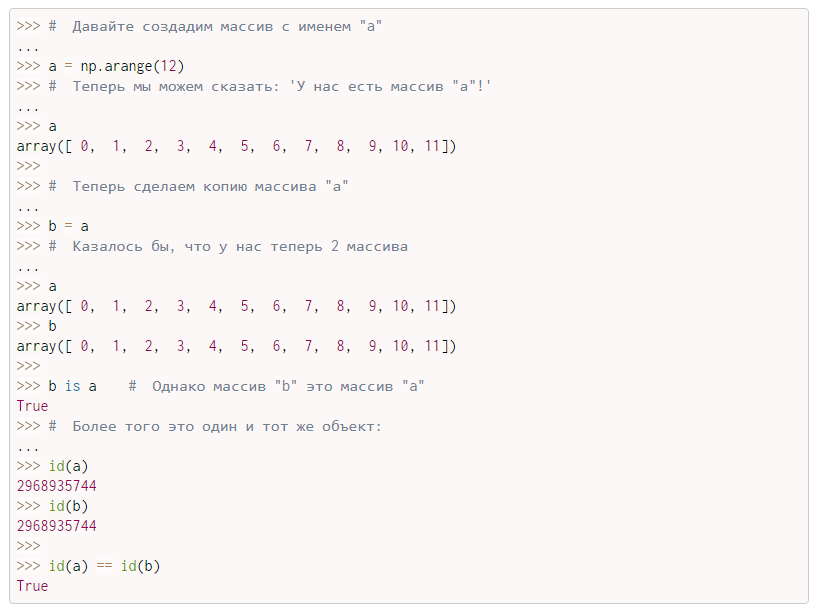
#4. Свойства и представления массивов, создание их копий | NumPy уроки

#5. Изменение формы массивов, добавление и удаление осей | NumPy уроки

#6. Объединение и разделение массивов | NumPy уроки

#7. Индексация, срезы, итерирование массивов | NumPy уроки

#8. Базовые математические операции над массивами | NumPy уроки

#9. Булевы операции и функции, значения inf и nan | NumPy уроки

#10. Базовые математические функции | NumPy уроки

#11. Произведение матриц и векторов, элементы линейной алгебры | NumPy уроки

#12. Множества (unique) и операции над ними | NumPy уроки

#13. Транслирование массивов | NumPy уроки

Добро пожаловать в NumPy!

NumPy (NumericalPython) — это библиотека Python с открытым исходным кодом, которая используется практически во всех областях науки и техники. Это универсальный стандарт для работы с числовыми данными в Python, и он лежит в основе научных экосистем Python и PyData. В число пользователей NumPy входят все — от начинающих программистов до опытных исследователей, занимающихся самыми современными научными и промышленными исследованиями и разработками. API-интерфейс NumPy широко используется в пакетах Pandas, SciPy, Matplotlib, scikit-learn, scikit-image и в большинстве других научных и научных пакетов Python.

Библиотека NumPy содержит многомерный массив и матричные структуры данных (дополнительную информацию об этом вы найдете в следующих разделах). Он предоставляет ndarray, однородный объект n-мерного массива, с методами для эффективной работы с ним. NumPy может использоваться для выполнения самых разнообразных математических операций над массивами. Он добавляет мощные структуры данных в Python, которые гарантируют эффективные вычисления с массивами и матрицами, и предоставляет огромную библиотеку математических функций высокого уровня, которые работают с этими массивами и матрицами.

Узнайте больше о NumPy здесь!

GIF черезgiphy

Установка NumPy

Чтобы установить NumPy, я настоятельно рекомендую использовать научный дистрибутив Python. Если вам нужны полные инструкции по установке NumPy в вашей операционной системе, вы можетенайти все детали здесь,

Если у вас уже есть Python, вы можете установить NumPy с помощью

conda install numpy

или

pip install numpy

Если у вас еще нет Python, вы можете рассмотреть возможность использованияанаконда, Это самый простой способ начать. Преимущество этого дистрибутива в том, что вам не нужно слишком беспокоиться об отдельной установке NumPy или каких-либо основных пакетов, которые вы будете использовать для анализа данных, таких как pandas, Scikit-Learn и т. Д.

Если вам нужна более подробная информация об установке, вы можете найти всю информацию об установке наscipy.org,

фотоАдриеннотPexels

Если у вас возникли проблемы с установкой Anaconda, вы можете ознакомиться с этой статьей:

Как импортировать NumPy

Каждый раз, когда вы хотите использовать пакет или библиотеку в своем коде, вам сначала нужно сделать его доступным.

Чтобы начать использовать NumPy и все функции, доступные в NumPy, вам необходимо импортировать его. Это можно легко сделать с помощью этого оператора импорта:

import numpy as np

(Мы сокращаем «numpy» до «np», чтобы сэкономить время и сохранить стандартизированный код, чтобы любой, кто работает с вашим кодом, мог легко его понять и запустить.)

В чем разница между списком Python и массивом NumPy?

NumPy предоставляет вам огромный выбор быстрых и эффективных числовых опций. Хотя список Python может содержать разные типы данных в одном списке, все элементы в массиве NumPy должны быть однородными. Математические операции, которые должны выполняться над массивами, были бы невозможны, если бы они не были однородными.

Зачем использовать NumPy?

фотоPixabayотPexels

Массивы NumPy быстрее и компактнее, чем списки Python. Массив потребляет меньше памяти и намного удобнее в использовании. NumPy использует гораздо меньше памяти для хранения данных и предоставляет механизм задания типов данных, который позволяет оптимизировать код еще дальше.

Что такое массив?

Массив является центральной структурой данных библиотеки NumPy. Это таблица значений, которая содержит информацию о необработанных данных, о том, как найти элемент и как интерпретировать элемент. Он имеет сетку элементов, которые можно проиндексировать в Все элементы имеют одинаковый тип, называемыймассив dtype(тип данных).

Массив может быть проиндексирован набором неотрицательных целых чисел, логическими значениями, другим массивом или целыми числами.рангмассива это количество измерений.формамассива — это кортеж целых чисел, дающий размер массива по каждому измерению.

Одним из способов инициализации массивов NumPy является использование вложенных списков Python.

a = np.array(, , ])

Мы можем получить доступ к элементам в массиве, используя квадратные скобки. Когда вы получаете доступ к элементам, помните, чтоиндексирование в NumPy начинается с 0, Это означает, что если вы хотите получить доступ к первому элементу в вашем массиве, вы получите доступ к элементу «0».

print(a)

Выход:

Массив

Массив numpy – это сетка значений одного типа. Мы можем инициализировать массив NumPy с помощью вложенного списка Python. Затем мы можем получить к ним доступ, используя их index. Также в NumPy есть функция, с помощью которой вы можете создавать различные типы массивов.

Смотрите следующий код, чтобы понять объявление массива numpy и доступ к элементам.

import numpy

# Create a rank 1 array
a = numpy.array()
print('print rank 1 array:')
# access the array using their index
print('print using their index: a= ', a)
a = 5  # modify the array
print('print using slicing : ', a)  # slicing can be used also
# print the whole list
print('Print the whole array : ', a)

# Create a rank 2 array using nested Python list
b = numpy.array(, ])
print('\nprint rank 2 array')
# access them using their index
print('print using their index: b= ', b, ' b= ',b)
print('print using slicing ', b)  # 1st slice for row, 2nd for column

# initialize a zero matrix
a = numpy.zeros((2, 2))
print('\nprint a 2-by-2 zero matrix:\n', a)

# Create an array of all ones
b = numpy.ones((2, 2))
print('\nprint a 2-by-2 all one matrix:\n', b)

# Create a constant array
c = numpy.full((3, 3), 6)
print('\nprint a 3-by-3 constant matrix for value = 6:\n', c)

# Create a 3x3 identity matrix
d = numpy.eye(3)
print('\nprint a 3-by-3 identity matrix:\n', d)

Результатом кода примера массива будет:

print rank 1 array:
print using their index: a=  3
print using slicing :  
Print the whole array :  

print rank 2 array
print using their index: b=  10  b=  20
print using slicing  `40 50`

print a 2-by-2 zero matrix:
 
 ]

print a 2-by-2 all one matrix:
 
 ]

print a 3-by-3 constant matrix for value = 6:
 
 
 ]

print a 3-by-3 identity matrix:
 
 
 ]

1.4.1.5. Indexing and slicing¶

The items of an array can be accessed and assigned to the same way as
other Python sequences (e.g. lists):

>>> a = np.arange(10)
>>> a
array()
>>> a], a2], a-1
(0, 2, 9)

Warning

Indices begin at 0, like other Python sequences (and C/C++).
In contrast, in Fortran or Matlab, indices begin at 1.

The usual python idiom for reversing a sequence is supported:

>>> a)

For multidimensional arrays, indices are tuples of integers:

>>> a = np.diag(np.arange(3))
>>> a
array(,
       ,
       ])
>>> a1, 1
1
>>> a2, 1 = 10 # third line, second column
>>> a
array(,
       ,
       ])
>>> a1
array()

Note

• In 2D, the first dimension corresponds to rows, the second
  to columns.
• for multidimensional , is interpreted by
  taking all elements in the unspecified dimensions.

Slicing: Arrays, like other Python sequences can also be sliced:

>>> a = np.arange(10)
>>> a
array()
>>> a293 # 
array()

Note that the last index is not included! :

>>> a)

All three slice components are not required: by default, start is 0,
end is the last and step is 1:

>>> a13
array()
>>> a)
>>> a3:]
array()

A small illustrated summary of NumPy indexing and slicing…

You can also combine assignment and slicing:

>>> a = np.arange(10)
>>> a5:] = 10
>>> a
array()
>>> b = np.arange(5)
>>> a5:] = b)

Exercise: Indexing and slicing

• Try the different flavours of slicing, using , and
  : starting from a linspace, try to obtain odd numbers
  counting backwards, and even numbers counting forwards.

• Reproduce the slices in the diagram above. You may
  use the following expression to create the array:

  >>> np.arange(6) + np.arange(, 51, 10),
         ,
         ,
         ,
         ,
         ])
  

Exercise: Array creation

Create the following arrays (with correct data types):

,
 1, 1, 1, 1],
 1, 1, 1, 2],
 1, 6, 1, 1]]

,
 2., , , , ],
 , 3., , , ],
 , , 4., , ],
 , , , 5., ],
 , , , , 6.]]

Par on course: 3 statements for each

Hint: Individual array elements can be accessed similarly to a list,
e.g. or .

Hint: Examine the docstring for .

max/ min:

Next, we have some more operations in numpy such as to find the minimum, maximum as well the sum of the numpy array. Let’s go ahead in python numpy tutorial and execute it practically.

import numpy as npa= np.array()print(a.min())print(a.max())print(a.sum())Output - 1 3 6

You must be finding these pretty basic, but with the help of this knowledge, you can perform a lot bigger tasks as well. Now, let’s understand the concept of axis in python numpy.

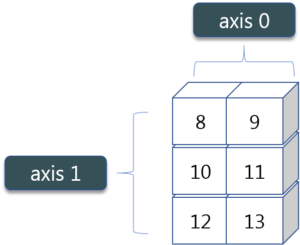
As you can see in the figure, we have a numpy array 2*3. Here the rows are called as axis 1 and the columns are called as axis 0. Now you must be wondering what is the use of these axis?

Suppose you want to calculate the sum of all the columns, then you can make use of axis. Let me show you practically, how you can implement axis in your PyCharm:

a= np.array()print(a.sum(axis=0))Output - 

Therefore, the sum of all the columns are added where 1+3=4, 2+4=6 and 3+5=8. Similarly, if you replace the axis by 1, then it will print where all the rows get added.

Manipulating NumPy Arrays

NumPy provides a method , which can be used to change the dimensions of the numpy array and modify the original array in place. Here, we show an illustration of using to change the shape of to

>>> c
array()
>>> c.shape
(12,)
>>> c.reshape(4, 3)
array(,
       ,
       ,
       ])

Since numpy operations are designed to be highly optimized, any subarray that is created from an array is still holding the reference to the original array. This means that if the subarray is modified in place, the original array is also modified.

>>> f = e
>>> f
array(,
       ,
       ])
>>> f *= 3
>>> f
array(,
       ,
       ])
>>> e
array(,
       ,
       ])

Here, the original array is also modified with any change in the subarray slice . This is because numpy slices only return a view of the original array.

To ensure that the original array is not modified with any change in the subarray slice, we use numpy method to create a copy of the array and modify the cloned object, instead of dealing with a reference of the original object.

The below snippet shows how deals with this issue.

>>> e
array(,
       ,
       ])
>>> f = e.copy()
>>> f
array(,
       ,
       ])
>>> f = 100
>>> f
array(,
       ,
       ])
>>> e
# No change is reflected in the original array
# We are safe!
array(,
       ,
       ])