How to use java math.random

Содержание:

Alternate API
Примеры использования модуля random.
Random Numbers Using the Math Class
- Random Numbers Within a Given Range
  - Random Double Within a Given Range
  - Random Integer Within a Given Range
Генерация случайного n-мерного массива вещественных чисел
Зачем нужны функции getstate() и setstate() ?
Alternate API
Генерация случайных распределений и псевдослучайных чисел в Python.
- Замечания по воспроизводимости последовательностей.
Java Math.random() Example
Линейный конгруэнтный ГПСЧ
Cryptographic Security
Math.Random() Example
Examples¶

Alternate API

There is an alternate API which may be easier to use, but may be less performant. In scenarios where performance is paramount, it is recommended to use the aforementioned API.

constrandom=newRandom(MersenneTwister19937.seedWithArray(0x12345678,0x90abcdef));constvalue=r.integer(,99);constotherRandom=newRandom();

This abstracts the concepts of engines and distributions.

: Produce an integer within the inclusive range . can be at its minimum -9007199254740992 (2 ** 53). can be at its maximum 9007199254740992 (2 ** 53). The special number is never returned.
: Produce a floating point number within the range . Uses 53 bits of randomness.
: Produce a boolean with a 50% chance of it being .
: Produce a boolean with the specified chance causing it to be .
: Produce a boolean with / chance of it being true.
: Return a random value within the provided within the sliced bounds of and .
: Shuffle the provided (in-place). Similar to .
: From the array, produce an array with elements that are randomly chosen without repeats.
: Same as
: Produce an array of length with as many rolls.
: Produce a random string using numbers, uppercase and lowercase letters, , and of length .
: Produce a random string using the provided string as the possible characters to choose from of length .
or : Produce a random string comprised of numbers or the characters of length .
: Produce a random string comprised of numbers or the characters of length .
: Produce a random within the inclusive range of . and must both be s.

Примеры использования модуля random.

Как сгенерировать случайное число в java

Базовое применение модуля:

>>> import random
# Случайное float:  0.0 <= x < 1.0
>>> random.random()
# 0.37444887175646646

# Случайное float:  2.5 <= x < 10.0
>>> random.uniform(2.5, 10.0)
# 3.1800146073117523

# Интервал между прибытием в среднем 5 секунд
>>> random.expovariate(1  5)
# 5.148957571865031

# Четное целое число от 0 до 100 включительно
>>> random.randrange(10)
# 7

# Even integer from 0 to 100 inclusive
>>> random.randrange(, 101, 2)
26

# Один случайный элемент из последовательности
>>> random.choice()
'draw'

>>> deck = 'ace two three four'.split()
# Перемешать список
>>> random.shuffle(deck)
>>> deck
'four', 'two', 'ace', 'three'

# Четыре образца без замены
>>> random.sample(, k=4)
#

Имитационные расчеты:

# Шесть вращений колеса рулетки (взвешенная выборка с заменой)
>>> choices(, 18, 18, 2], k=6)
# 

# Сдайте 20 карт без замены из колоды из 52 игральных карт
# и определите пропорцию карт с достоинством в: 
# десять, валет, дама или король.
>>> dealt = sample(, counts=16, 36], k=20)
>>> dealt.count('tens')  20
# 0.15

# Оценка вероятности получения 5 или более попаданий из 7 
# бросаний монеты, которая выпадает орлом в 60% случаев.
>>> def trial():
...     return choices('HT', cum_weights=(0.60, 1.00), k=7).count('H') >= 5
...
>>> sum(trial() for i in range(10_000))  10_000
# 0.4169

>>> # Вероятность того, что медиана из 5 выборок находится в средних двух квартилях
>>> def trial():
...     return 2_500 <= sorted(choices(range(10_000), k=5))[2 < 7_500
...
>>> sum(trial() for i in range(10_000))  10_000
# 0.7958

Пример статистической начальной загрузки с использованием повторной выборки с заменой для оценки доверительного интервала для среднего значения выборки:

# http://statistics.about.com/od/Applications/a/Example-Of-Bootstrapping.htm
from statistics import fmean as mean
from random import choices

data = 41, 50, 29, 37, 81, 30, 73, 63, 20, 35, 68, 22, 60, 31, 95
means = sorted(mean(choices(data, k=len(data))) for i in range(100))
print(f'The sample mean of {mean(data).1f} has a 90% confidence '
      f'interval from {means5.1f} to {means94.1f}')

Пример теста перестановки повторной выборки для определения статистической значимости или Р-значения наблюдаемой разницы между эффектами препарата и плацебо:

# Example from "Statistics is Easy" by Dennis Shasha and Manda Wilson
from statistics import fmean as mean
from random import shuffle

drug = 54, 73, 53, 70, 73, 68, 52, 65, 65
placebo = 54, 51, 58, 44, 55, 52, 42, 47, 58, 46
observed_diff = mean(drug) - mean(placebo)

n = 10_000
count = 
combined = drug + placebo
for i in range(n):
    shuffle(combined)
    new_diff = mean(combined) - mean(combinedlen(drug):])
    count += (new_diff >= observed_diff)

print(f'{n} label reshufflings produced only {count} instances with a difference')
print(f'at least as extreme as the observed difference of {observed_diff.1f}.')
print(f'The one-sided p-value of {count  n.4f} leads us to reject the null')
print(f'hypothesis that there is no difference between the drug and the placebo.')

Моделирование времени прибытия и доставки услуг для многосерверной очереди:

from heapq import heappush, heappop
from random import expovariate, gauss
from statistics import mean, median, stdev

average_arrival_interval = 5.6
average_service_time = 15.0
stdev_service_time = 3.5
num_servers = 3

waits = []
arrival_time = 0.0
servers = 0.0 * num_servers  # time when each server becomes available
for i in range(100_000):
    arrival_time += expovariate(1.0  average_arrival_interval)
    next_server_available = heappop(servers)
    wait = max(0.0, next_server_available - arrival_time)
    waits.append(wait)
    service_duration = gauss(average_service_time, stdev_service_time)
    service_completed = arrival_time + wait + service_duration
    heappush(servers, service_completed)

print(f'Mean wait: {mean(waits).1f}.  Stdev wait: {stdev(waits).1f}.')
print(f'Median wait: {median(waits).1f}.  Max wait: {max(waits).1f}.')

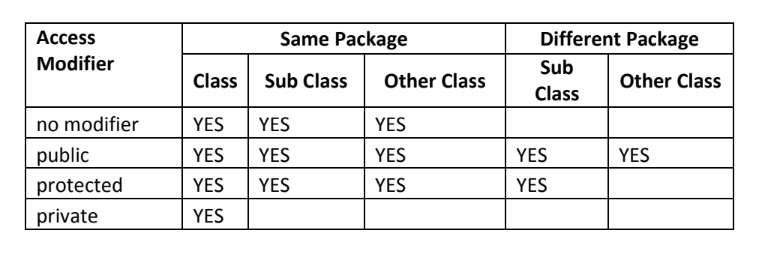
Random Numbers Using the Math Class

Изучаем java: сравнение строк

Java provides the Math class in the java.util package to generate random numbers.

The Math class contains the static Math.random() method to generate random numbers of the double type.

The random() method returns a double value with a positive sign, greater than or equal to 0.0 and less than 1.0. When you call Math.random(), under the hood, a java.util.Random pseudorandom-number generator object is created and used.

You can use the Math.random() method with or without passing parameters. If you provide parameters, the method produces random numbers within the given parameters.

The code to use the Math.random() method:

The getRandomNumber() method uses the Math.random() method to return a positive double value that is greater than or equal to 0.0 and less than 1.0.

The output of running the code is:

Random Numbers Within a Given Range

For generating random numbers between a given a range, you need to specify the range. A standard expression for accomplishing this is:

Let us break this expression into steps:

First, multiply the magnitude of the range of values you want to cover by the result that Math.random() produces.returns a value in the range ,max–min where max is excluded. For example, if you want 5,10], you need to cover 5 integer values so you can use Math.random()*5. This would return a value in the range ,5, where 5 is not included.
Next, shift this range up to the range that you are targeting. You do this by adding the min value.

But this still does not include the maximum value.

To get the max value included, you need to add 1 to your range parameter (max — min). This will return a random double within the specified range.

There are different ways of implementing the above expression. Let us look at a couple of them.

Random Double Within a Given Range

By default, the Math.random() method returns a random number of the type double whenever it is called. The code to generate a random double value between a specified range is:

You can call the preceding method from the main method by passing the arguments like this.

The output is this.

Random Integer Within a Given Range

The code to generate a random integer value between a specified range is this.

The preceding getRandomIntegerBetweenRange() method produces a random integer between the given range. As Math.random() method generates random numbers of double type, you need to truncate the decimal part and cast it to int in order to get the integer random number. You can call this method from the main method by passing the arguments as follows:

The output is this.

Note: You can pass a range of negative values to generate a random negative number within the range.

Генерация случайного n-мерного массива вещественных чисел

Использование для генерации n-мерного массива случайных вещественных чисел в пределах
Использование для генерации n-мерного массива случайных вещественных чисел в пределах

Класс integer в java

Python

import numpy

random_float_array = numpy.random.rand(2, 2)
print(«2 X 2 массив случайных вещественных чисел в \n», random_float_array,»\n»)

random_float_array = numpy.random.uniform(25.5, 99.5, size=(3, 2))
print(«3 X 2 массив случайных вещественных чисел в \n», random_float_array,»\n»)

1
2
3
4
5
6
7
8

importnumpy

random_float_array=numpy.random.rand(2,2)

print(«2 X 2 массив случайных вещественных чисел в \n»,random_float_array,»\n»)

random_float_array=numpy.random.uniform(25.5,99.5,size=(3,2))

print(«3 X 2 массив случайных вещественных чисел в \n»,random_float_array,»\n»)

Вывод:

Shell

2 X 2 массив случайных вещественных чисел в

]

3 X 2 массив случайных вещественных чисел в

]

1
2
3
4
5
6
7
8

2X2массивслучайныхвещественныхчиселв0.0,1.0

0.089385930.89085866

0.473071690.41401363

3X2массивслучайныхвещественныхчиселв25.5,99.5

55.405785465.60206715

91.6218540484.16144062

44.34825227.28381058

Зачем нужны функции getstate() и setstate() ?

Если вы получили предыдущее состояние и восстановили его, тогда вы сможете оперировать одними и теми же случайными данными раз за разом. Помните, что использовать другую функцию random в данном случае нельзя. Также нельзя изменить значения заданных параметров. Сделав это, вы измените значение состояния .

Для закрепления понимания принципов работы и в генераторе случайных данных Python рассмотрим следующий пример:

Python

import random

number_list =

print(«Первая выборка «, random.sample(number_list,k=5))

# хранит текущее состояние в объекте state
state = random.getstate()

print(«Вторая выборка «, random.sample(number_list,k=5))

# Восстанавливает состояние state, используя setstate
random.setstate(state)

#Теперь будет выведен тот же список второй выборки
print(«Третья выборка «, random.sample(number_list,k=5))

# Восстанавливает текущее состояние state
random.setstate(state)

# Вновь будет выведен тот же список второй выборки
print(«Четвертая выборка «, random.sample(number_list,k=5))

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23

importrandom

number_list=3,6,9,12,15,18,21,24,27,30

print(«Первая выборка «,random.sample(number_list,k=5))

# хранит текущее состояние в объекте state

state=random.getstate()

print(«Вторая выборка «,random.sample(number_list,k=5))

# Восстанавливает состояние state, используя setstate

random.setstate(state)

#Теперь будет выведен тот же список второй выборки

print(«Третья выборка «,random.sample(number_list,k=5))

# Восстанавливает текущее состояние state

random.setstate(state)

# Вновь будет выведен тот же список второй выборки

print(«Четвертая выборка «,random.sample(number_list,k=5))

Вывод:

Shell

Первая выборка
Вторая выборка
Третья выборка
Четвертая выборка

1
2
3
4

Перваявыборка18,15,30,9,6

Втораявыборка27,15,12,9,6

Третьявыборка27,15,12,9,6

Четвертаявыборка27,15,12,9,6

Как можно заметить в результате вывода — мы получили одинаковые наборы данных. Это произошло из-за сброса генератора случайных данных.

Alternate API

There is an alternate API which may be easier to use, but may be less performant. In scenarios where performance is paramount, it is recommended to use the aforementioned API.

const random = new Random(
  MersenneTwister19937.seedWithArray(0x12345678, 0x90abcdef)
);
const value = r.integer(, 99);

const otherRandom = new Random(); // same as new Random(nativeMath)

This abstracts the concepts of engines and distributions.

: Produce an integer within the inclusive range . can be at its minimum -9007199254740992 (2 ** 53). can be at its maximum 9007199254740992 (2 ** 53). The special number is never returned.
: Produce a floating point number within the range . Uses 53 bits of randomness.
: Produce a boolean with a 50% chance of it being .
: Produce a boolean with the specified chance causing it to be .
: Produce a boolean with / chance of it being true.
: Return a random value within the provided within the sliced bounds of and .
: Shuffle the provided (in-place). Similar to .
: From the array, produce an array with elements that are randomly chosen without repeats.
: Same as
: Produce an array of length with as many rolls.
: Produce a random string using numbers, uppercase and lowercase letters, , and of length .
: Produce a random string using the provided string as the possible characters to choose from of length .
or : Produce a random string comprised of numbers or the characters of length .
: Produce a random string comprised of numbers or the characters of length .
: Produce a random within the inclusive range of . and must both be s.

Генерация случайных распределений и псевдослучайных чисел в Python.

Модуль реализует генераторы псевдослучайных чисел для различных распределений.

Для целых чисел существует равномерный выбор из диапазона. Для последовательностей существует равномерный выбор случайного элемента, функция для генерации случайной перестановки списка на месте и функция для случайной выборки без замены.

На реальной линии есть функции для вычисления равномерного, нормального (гауссовского), логнормального, отрицательного экспоненциального, гамма и бета распределений. Для генерации распределений углов доступно распределение фон Мизеса.

Почти все функции модуля зависят от базовой функции , которая генерирует случайное число с плавающей точкой в полуоткрытом диапазоне . Python использует Mersenne Twister в качестве генератора ядра. Он генерирует 53-битные значения точности и имеет период . Базовая реализация в C является быстрой и поточно-ориентированной. Mersenne Twister является одним из наиболее тщательно протестированных генераторов случайных чисел из существующих. Однако, будучи полностью детерминированным, он не подходит для всех целей и совершенно не подходит для криптографических целей.

Функции, предоставляемые этим модулем, на самом деле являются связанными методами скрытого экземпляра класса . Вы можете создать свои собственные экземпляры , чтобы получить генераторы, которые не делятся состоянием.

Класс также можно разделить на подклассы, если вы хотите использовать другой базовый генератор вашего собственного устройства: в этом случае переопределите методы , , и . При желании новый генератор может предоставить метод — это позволяет производить выборки в произвольно большом диапазоне.

Модуль также предоставляет класс , который использует системную функцию для генерации случайных чисел из источников, предоставляемых операционной системой.

Предупреждение.

Псевдослучайные генераторы этого модуля не должны использоваться в целях безопасности. В целях безопасности или криптографического использования смотрите «Модуль «.

Замечания по воспроизводимости последовательностей.

Иногда полезно иметь возможность воспроизвести последовательности, заданные генератором псевдослучайных чисел. При повторном использовании начального значения , одна и та же последовательность должна воспроизводиться от запуска к запуску, пока не запущено несколько потоков.

Большинство алгоритмов и функций модуля могут изменяться в разных версиях Python, но два аспекта гарантированно не изменятся:

Если будет добавлен новый метод, то обязательно будет предложена обратная совместимость.
Метод генератора будет продолжать создавать ту же последовательность, если совместимому методу будет дано то же самое начальное число .

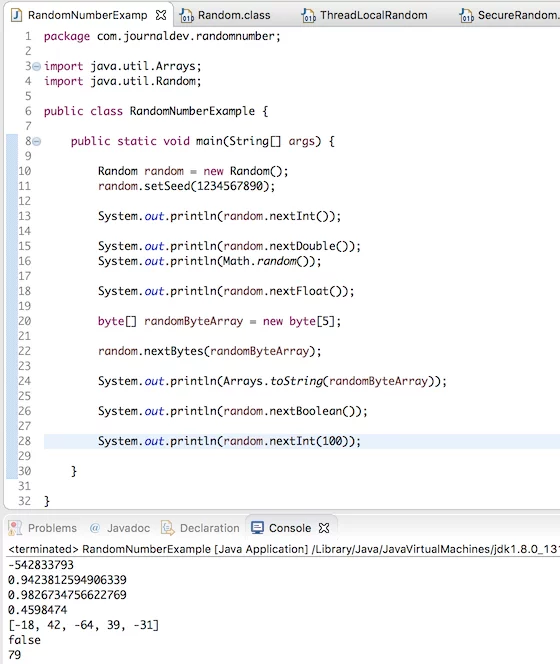
Java Math.random() Example

Java program to demonstrate Math.random() method. We will take a loop and call the Math.random() method multiple times. In each execution, it gives a different double value with a positive sign, greater than or equal to 0.0 and less than 1.0.

Output:-

0.61921576963401330.08796048507589238

Each time we get different floating-point values ranges from 0.0 to 1.0.

Note:- There are infinite floating-point numbers are possible between 0.0 to 1.0, but double data type gives only up to 15 to 16 decimal point precision.

If we import the Math class statically and then we can invoke random() method without calling through it’s class name.

Output:-

0.2644603504223617

The “import static java.lang.Math.*;” statement will import all static members of the Math class. But if we want to import only the random() method of the Math class, not another static method and variables of Math class then we can use the “import static java.lang.Math.random;” statement. Learn more about static import in Java

Линейный конгруэнтный ГПСЧ

Линейный конгруэнтный ГПСЧ(LCPRNG) — это распространённый метод для генерации псевдослучайных чисел. Он не обладает криптографической стойкостью. Этот метод заключается в вычислении членов линейной рекуррентной последовательности по модулю некоторого натурального числа m, задаваемой формулой. Получаемая последовательность зависит от выбора стартового числа — т.е. seed. При разных значениях seed получаются различные последовательности случайных чисел. Пример реализации такого алгоритма на JavaScript:

Многие языки программирования используют LСPRNG (но не именно такой алгоритм(!)).

Как говорилось выше, такую последовательность можно предсказать. Так зачем нам ГПСЧ? Если говорить про безопасность, то ГПСЧ — это проблема. Если говорить про другие задачи, то эти свойства — могут сыграть в плюс. Например для различных спец эффектов и анимаций графики может понадобиться частый вызов random. И вот тут важны распределение значений и перформанс! Секурные алгоритмы не могут похвастать скоростью работы.

Еще одно свойство — воспроизводимость. Некоторые реализации позволяют задать seed, и это очень полезно, если последовательность должна повторяться. Воспроизведение нужно в тестах, например. И еще много других вещей существует, для которых не нужен безопасный ГСЧ.

Cryptographic Security

Some applications require cryptographic level of security in the random number generation. What this means is that the generator must pass tests outlined in section 4.9.1 of this document. You can generate cryptographically secure random numbers using the class SecureRandom.

Implementations of the SecureRandom class might generate pseudo random numbers; this implementation uses a deterministic algorithm (or formula) to produce pseudo random numbers. Some implementations may produce true random numbers while others might use a combination of the two.

Running the following code two times on my machine produced the output shown. Even when the generator is being initialized with a known seed, it produces different sequences. Does that mean the sequence is truly random? The answer lies in how the RNG is initialized. SecureRandom combines the user-specified seed with some random bits from the system. This results in a different sequence even when the seed is set to a known value. Random, on the other hand, just replaces the seed with the user specified value.

Math.Random() Example

Here’s an example of the method in action:

import java.lang.Math;

class Main {
	public static void main(String[] args) {
		double number = Math.random();
		System.out.println("Random number: " + number);
	}
}

Our code returns:

As you can see, our program has returned a random number between 0 and 1. However, this number is not very useful in its current form. If we want to generate a random number for a guessing game, for instance, we would not want to have a decimal number.

In order to produce a whole number with our pseudorandom number generator, we can multiply our random number by another number and round it to the nearest whole number. For instance, suppose we wanted to generate a random number between 1 and 10. We could do so using this code:

class Main {
	public static void main(String[] args) {
		int number = (int)(Math.random() * 10);
		System.out.println("Random number: " + number);
	}
}

Here is the result of our program after running it three times:

As you can see, our program returns a random integer, or whole number.

Let’s break down our code. First, we declared a class called Main which stores the code for our program.

Then we used the method to generate a random number, and we multiplied that number by 10. After we multiplied the result by 10, we converted it to an integer, which rounds it to the nearest decimal place and gives us a whole number.

Then, on the final line, we print out the message “Random number: “ to the console, followed by the random number our program generated.

If we wanted to generate a larger number, we could replace the * 10 parts of our code with another number. For instance, say we wanted to generate a number between 1 and 1000. We could do so by replacing * 10 with * 1000 like this:

class Main {
	public static void main(String[] args) {
		int number = (int)(Math.random() * 1000);
		System.out.println("Random number: " + number);
	}
}

After executing our program three times, the following response was returned:

181

914

939

Examples¶

Basic examples:

>>> random()                             # Random float:  0.0 <= x < 1.0
0.37444887175646646

>>> uniform(2.5, 10.0)                   # Random float:  2.5 <= x < 10.0
3.1800146073117523

>>> expovariate(1  5)                   # Interval between arrivals averaging 5 seconds
5.148957571865031

>>> randrange(10)                        # Integer from 0 to 9 inclusive
7

>>> randrange(, 101, 2)                 # Even integer from 0 to 100 inclusive
26

>>> choice()      # Single random element from a sequence
'draw'

>>> deck = 'ace two three four'.split()
>>> shuffle(deck)                        # Shuffle a list
>>> deck


>>> sample(, k=4)    # Four samples without replacement

Simulations:

>>> # Six roulette wheel spins (weighted sampling with replacement)
>>> choices(, 18, 18, 2], k=6)


>>> # Deal 20 cards without replacement from a deck
>>> # of 52 playing cards, and determine the proportion of cards
>>> # with a ten-value:  ten, jack, queen, or king.
>>> dealt = sample(, counts=16, 36], k=20)
>>> dealt.count('tens')  20
0.15

>>> # Estimate the probability of getting 5 or more heads from 7 spins
>>> # of a biased coin that settles on heads 60% of the time.
>>> def trial():
...     return choices('HT', cum_weights=(0.60, 1.00), k=7).count('H') >= 5
...
>>> sum(trial() for i in range(10_000))  10_000
0.4169

>>> # Probability of the median of 5 samples being in middle two quartiles
>>> def trial():
...     return 2_500 <= sorted(choices(range(10_000), k=5))[2 < 7_500
...
>>> sum(trial() for i in range(10_000))  10_000
0.7958

Example of statistical bootstrapping using resampling
with replacement to estimate a confidence interval for the mean of a sample:

# http://statistics.about.com/od/Applications/a/Example-Of-Bootstrapping.htm
from statistics import fmean as mean
from random import choices

data = 41, 50, 29, 37, 81, 30, 73, 63, 20, 35, 68, 22, 60, 31, 95
means = sorted(mean(choices(data, k=len(data))) for i in range(100))
print(f'The sample mean of {mean(data).1f} has a 90% confidence '
      f'interval from {means5.1f} to {means94.1f}')

Example of a
to determine the statistical significance or p-value of an observed difference
between the effects of a drug versus a placebo:

# Example from "Statistics is Easy" by Dennis Shasha and Manda Wilson
from statistics import fmean as mean
from random import shuffle

drug = 54, 73, 53, 70, 73, 68, 52, 65, 65
placebo = 54, 51, 58, 44, 55, 52, 42, 47, 58, 46
observed_diff = mean(drug) - mean(placebo)

n = 10_000
count = 
combined = drug + placebo
for i in range(n):
    shuffle(combined)
    new_diff = mean(combined) - mean(combinedlen(drug):])
    count += (new_diff >= observed_diff)

print(f'{n} label reshufflings produced only {count} instances with a difference')
print(f'at least as extreme as the observed difference of {observed_diff.1f}.')
print(f'The one-sided p-value of {count  n.4f} leads us to reject the null')
print(f'hypothesis that there is no difference between the drug and the placebo.')

Simulation of arrival times and service deliveries for a multiserver queue:

from heapq import heappush, heappop
from random import expovariate, gauss
from statistics import mean, median, stdev

average_arrival_interval = 5.6
average_service_time = 15.0
stdev_service_time = 3.5
num_servers = 3

waits = []
arrival_time = 0.0
servers = 0.0 * num_servers  # time when each server becomes available
for i in range(100_000):
    arrival_time += expovariate(1.0  average_arrival_interval)
    next_server_available = heappop(servers)
    wait = max(0.0, next_server_available - arrival_time)
    waits.append(wait)
    service_duration = gauss(average_service_time, stdev_service_time)
    service_completed = arrival_time + wait + service_duration
    heappush(servers, service_completed)

print(f'Mean wait: {mean(waits).1f}.  Stdev wait: {stdev(waits).1f}.')
print(f'Median wait: {median(waits).1f}.  Max wait: {max(waits).1f}.')