Python array with examples

Implementing MergeSort and QuickSort

Here, we investigate two other commonly used Sorting techniques used in actual practice, namely the MergeSort and the QuickSort algorithms.

1. MergeSort Algorithm

The algorithm uses a bottom-up Divide and Conquer approach, first dividing the original array into subarrays and then merging the individually sorted subarrays to yield the final sorted array.

In the below code snippet, the method does the actual splitting into subarrays and the perform_merge() method merges two previously sorted arrays into a new sorted array.

import array

def mergesort(a, arr_type):
    def perform_merge(a, arr_type, start, mid, end):
        # Merges two previously sorted arrays
        # a and a
        tmp = array.array(arr_type, )
        def compare(tmp, i, j):
            if tmp <= tmp:
                i += 1
                return tmp
            else:
                j += 1
                return tmp
        i = start
        j = mid + 1
        curr = start
        while i<=mid or j<=end:
            if i<=mid and j<=end:
                if tmp <= tmp:
                    a = tmp
                    i += 1
                else:
                    a = tmp
                    j += 1
            elif i==mid+1 and j<=end:
                a = tmp
                j += 1
            elif j == end+1 and i<=mid:
                a = tmp
                i += 1
            elif i > mid and j > end:
                break
            curr += 1


    def mergesort_helper(a, arr_type, start, end):
        # Divides the array into two parts
        # recursively and merges the subarrays
        # in a bottom up fashion, sorting them
        # via Divide and Conquer
        if start < end:
            mergesort_helper(a, arr_type, start, (end + start)//2)
            mergesort_helper(a, arr_type, (end + start)//2 + 1, end)
            perform_merge(a, arr_type, start, (start + end)//2, end)


    # Sorts the array using mergesort_helper
    mergesort_helper(a, arr_type, 0, len(a)-1)

Test Case:

a = array.array('i', )
print('Before MergeSort ->', a)
mergesort(a, 'i')
print('After MergeSort ->', a)

Output:

Before MergeSort -> array('i', )
After MergeSort -> array('i', )

2. QuickSort Algorithm

This algorithm also uses a Divide and Conquer strategy, but uses a top-down approach instead, first partitioning the array around a pivot element (here, we always choose the last element of the array to be the pivot).

Thus ensuring that after every step, the pivot is at its designated position in the final sorted array.

After ensuring that the array is partitioned around the pivot (Elements lesser than the pivot are to the left, and the elements which are greater than the pivot are to the right), we continue applying the function to the rest of the array, until all the elements are at their respective position, which is when the array is completely sorted.

Note: There are other approaches to this algorithm for choosing the pivot element. Some variants choose the median element as the pivot, while others make use of a random selection strategy for the pivot.

def quicksort(a, arr_type):
    def do_partition(a, arr_type, start, end):
        # Performs the partitioning of the subarray a
        
        # We choose the last element as the pivot
        pivot_idx = end
        pivot = a

        # Keep an index for the first partition
        # subarray (elements lesser than the pivot element)
        idx = start - 1

        def increment_and_swap(j):
            nonlocal idx
            idx += 1
            a, a = a, a

         < pivot]
        
        # Finally, we need to swap the pivot (a with a)
        # since we have reached the position of the pivot in the actual
        # sorted array
        a, a = a, a

        # Return the final updated position of the pivot
        # after partitioning
        return idx+1

    def quicksort_helper(a, arr_type, start, end):
        if start < end:
            # Do the partitioning first and then go via
            # a top down divide and conquer, as opposed
            # to the bottom up mergesort
            pivot_idx = do_partition(a, arr_type, start, end)
            quicksort_helper(a, arr_type, start, pivot_idx-1)
            quicksort_helper(a, arr_type, pivot_idx+1, end)

    quicksort_helper(a, arr_type, 0, len(a)-1)

Here, the method does the step of the Divide and Conquer approach, while the method partitions the array around the pivot and returns the position of the pivot, around which we continue to recursively partition the subarray before and after the pivot until the entire array is sorted.

Test Case:

b = array.array('i', )
print('Before QuickSort ->', b)
quicksort(b, 'i')
print('After QuickSort ->', b)

Output:

Before QuickSort -> array('i', )
After QuickSort -> array('i', )

Массив нарезки

Все идет нормально; Создание и индексация массивов выглядит знакомо.

Теперь мы подошли к нарезке массивов, и это одна из функций, которая создает проблемы для начинающих массивов Python и NumPy.

Структуры, такие как списки и массивы NumPy, могут быть нарезаны. Это означает, что подпоследовательность структуры может быть проиндексирована и извлечена.

Это наиболее полезно при машинном обучении при указании входных и выходных переменных или разделении обучающих строк из строк тестирования.

Нарезка задается с помощью оператора двоеточия ‘:’ с ‘от’ а также ‘в‘Индекс до и после столбца соответственно. Срез начинается от индекса «от» и заканчивается на один элемент перед индексом «до».

Давайте рассмотрим несколько примеров.

Одномерная нарезка

Вы можете получить доступ ко всем данным в измерении массива, указав срез «:» без индексов.

При выполнении примера печатаются все элементы в массиве.

Первый элемент массива можно разрезать, указав фрагмент, который начинается с индекса 0 и заканчивается индексом 1 (один элемент перед индексом «до»)

Выполнение примера возвращает подмассив с первым элементом.

Мы также можем использовать отрицательные индексы в срезах. Например, мы можем нарезать последние два элемента в списке, начав срез с -2 (второй последний элемент) и не указав индекс «до»; это берет ломтик до конца измерения.

Выполнение примера возвращает подмассив только с двумя последними элементами.

Двумерная нарезка

Давайте рассмотрим два примера двумерного среза, которые вы, скорее всего, будете использовать в машинном обучении.

Разделение функций ввода и вывода

Распространено загруженные данные на входные переменные (X) и выходную переменную (y).

Мы можем сделать это, разрезая все строки и все столбцы до, но перед последним столбцом, затем отдельно индексируя последний столбец.

Для входных объектов мы можем выбрать все строки и все столбцы, кроме последнего, указав ‘:’ в индексе строк и: -1 в индексе столбцов.

Для выходного столбца мы можем снова выбрать все строки, используя ‘:’, и индексировать только последний столбец, указав индекс -1.

Собрав все это вместе, мы можем разделить 3-колоночный 2D-набор данных на входные и выходные данные следующим образом:

При выполнении примера печатаются разделенные элементы X и y

Обратите внимание, что X — это двумерный массив, а y — это одномерный массив

Сплит поезд и тестовые ряды

Обычно загруженный набор данных разбивают на отдельные наборы поездов и тестов.

Это разделение строк, где некоторая часть будет использоваться для обучения модели, а оставшаяся часть будет использоваться для оценки мастерства обученной модели.

Для этого потребуется разрезать все столбцы, указав «:» во втором индексе измерения. Набор обучающих данных будет содержать все строки от начала до точки разделения.

Тестовым набором данных будут все строки, начиная с точки разделения до конца измерения.

Собрав все это вместе, мы можем разделить набор данных в надуманной точке разделения 2.

При выполнении примера выбираются первые две строки для обучения и последняя строка для набора тестов.

Ways to Print an Array in Python

Now, let us look at some of the ways to print both 1D as well as 2D arrays in Python. Note: these arrays are going to be implemented using lists.

Directly printing using the print() method

We can directly pass the name of the array(list) containing the values to be printed to the method in Python to print the same.

But in this case, the array is printed in the form of a list i.e. with brackets and values separated by commas.

arr = 
arr_2d = ,]

print("The Array is: ", arr) #printing the array
print("The 2D-Array is: ", arr_2d) #printing the 2D-Array

Output:

The Array is:  
The 2D-Array is:  , ]

Here, is a one-dimensional array. Whereas, is a two-dimensional one. We directly pass their respective names to the method to print them in the form of a list and list of lists respectively.

Using for loops in Python

We can also print an array in Python by traversing through all the respective elements using loops.

Let us see how.

arr = 
arr_2d = ,]

#printing the array
print("The Array is : ")
for i in arr:
    print(i, end = ' ')

#printing the 2D-Array
print("\nThe 2D-Array is:")
for i in arr_2d:
    for j in i:
        print(j, end=" ")
    print()

Output:

The Array is : 
2 4 5 7 9 
The 2D-Array is:
1 2 
3 4

In the code above we traverse through the elements of a 1D as well as a 2D Array using for loops and print the corresponding elements in our desired form.

Reverse a List Array in Python

As we already discussed Lists and Arrays are similar in Python. Where the major difference among the two is that arrays only allow items of the same data type whereas lists allow them to be different.

Since Python doesn’t support conventional Arrays, we can use lists to depict the same and try to reverse them. Let us take a look at the different methods following which we can accomplish this task,

1. Using List Slicing to Reverse an Array in Python

We can reverse a list array using slicing methods. In this way, we actually create a new list in the reverse order as that of the original one. Let us see how:

#The original array
arr = 
print("Array is :",arr)

res = arr #reversing using list slicing
print("Resultant new reversed array:",res)

Output:

Array is : 
Resultant new reversed array: 

2. Using reverse() Method

Python also provides a built-in method that directly reverses the order of list items right at the original place.

Note: In this way, we change the order of the actual list. Hence, the original order is lost.

#The original array
arr = 
print("Before reversal Array is :",arr)

arr.reverse() #reversing using reverse()
print("After reversing Array:",arr)

Output:

Before reversal Array is : 
After reversing Array: 

3. Using reversed() Method

We have yet another method, which when passed with a list returns an iterable having just items of the list in reverse order. If we use the method on this iterable object, we get a new list which contains our reversed array.

#The original array
arr = 
print("Original Array is :",arr)
#reversing using reversed()
result=list(reversed(arr))
print("Resultant new reversed Array:",result)

Output:

Original Array is : 
Resultant new reversed Array: 

Присваивание не копирует массивы в Python

Итак, простое присваивание никаких копий массива не выполняет, и это первое, что стоит уяснить. Может показаться, что это всего лишь прихоть создателей Python и NumPy, но всё не так просто. Если бы ситуация обстояла иначе, мы бы работали с памятью напрямую, а отсутствие автоматического копирования во время присваивания — совсем небольшая плата за лёгкость и простоту языка программирования Python.

Давайте приведём ещё парочку примеров на эту тему:

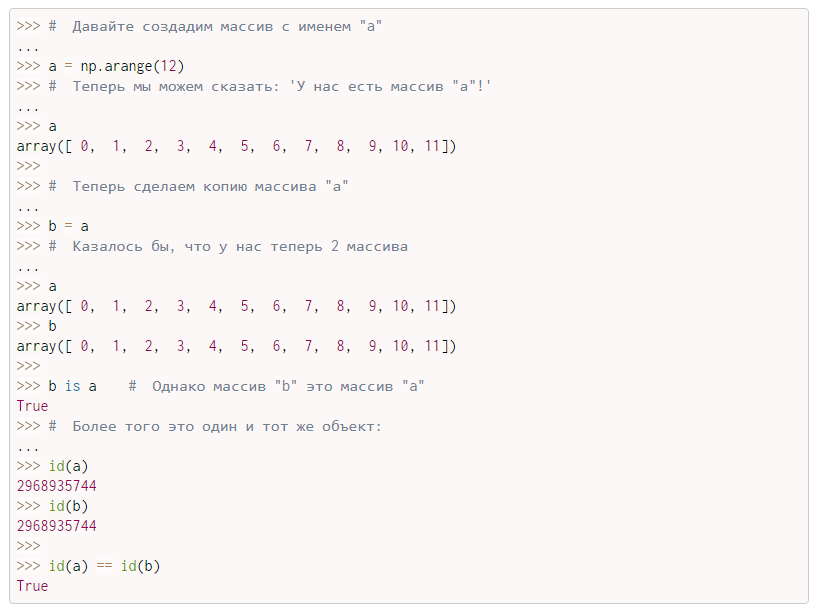
Обратите внимание, что массивы a и b в действительности являются одним и тем же массивом с такими же данными и типом данных

Таким образом, у нас есть массив b и массив a, но нельзя забывать о том, что это, по сути, один и тот же массив.

Добро пожаловать в NumPy!

NumPy (NumericalPython) — это библиотека Python с открытым исходным кодом, которая используется практически во всех областях науки и техники. Это универсальный стандарт для работы с числовыми данными в Python, и он лежит в основе научных экосистем Python и PyData. В число пользователей NumPy входят все — от начинающих программистов до опытных исследователей, занимающихся самыми современными научными и промышленными исследованиями и разработками. API-интерфейс NumPy широко используется в пакетах Pandas, SciPy, Matplotlib, scikit-learn, scikit-image и в большинстве других научных и научных пакетов Python.

Библиотека NumPy содержит многомерный массив и матричные структуры данных (дополнительную информацию об этом вы найдете в следующих разделах). Он предоставляет ndarray, однородный объект n-мерного массива, с методами для эффективной работы с ним. NumPy может использоваться для выполнения самых разнообразных математических операций над массивами. Он добавляет мощные структуры данных в Python, которые гарантируют эффективные вычисления с массивами и матрицами, и предоставляет огромную библиотеку математических функций высокого уровня, которые работают с этими массивами и матрицами.

Узнайте больше о NumPy здесь!

GIF черезgiphy

Установка NumPy

Чтобы установить NumPy, я настоятельно рекомендую использовать научный дистрибутив Python. Если вам нужны полные инструкции по установке NumPy в вашей операционной системе, вы можетенайти все детали здесь,

Если у вас уже есть Python, вы можете установить NumPy с помощью

conda install numpy

или

pip install numpy

Если у вас еще нет Python, вы можете рассмотреть возможность использованияанаконда, Это самый простой способ начать. Преимущество этого дистрибутива в том, что вам не нужно слишком беспокоиться об отдельной установке NumPy или каких-либо основных пакетов, которые вы будете использовать для анализа данных, таких как pandas, Scikit-Learn и т. Д.

Если вам нужна более подробная информация об установке, вы можете найти всю информацию об установке наscipy.org,

фотоАдриеннотPexels

Если у вас возникли проблемы с установкой Anaconda, вы можете ознакомиться с этой статьей:

Как импортировать NumPy

Каждый раз, когда вы хотите использовать пакет или библиотеку в своем коде, вам сначала нужно сделать его доступным.

Чтобы начать использовать NumPy и все функции, доступные в NumPy, вам необходимо импортировать его. Это можно легко сделать с помощью этого оператора импорта:

import numpy as np

(Мы сокращаем «numpy» до «np», чтобы сэкономить время и сохранить стандартизированный код, чтобы любой, кто работает с вашим кодом, мог легко его понять и запустить.)

В чем разница между списком Python и массивом NumPy?

NumPy предоставляет вам огромный выбор быстрых и эффективных числовых опций. Хотя список Python может содержать разные типы данных в одном списке, все элементы в массиве NumPy должны быть однородными. Математические операции, которые должны выполняться над массивами, были бы невозможны, если бы они не были однородными.

Зачем использовать NumPy?

фотоPixabayотPexels

Массивы NumPy быстрее и компактнее, чем списки Python. Массив потребляет меньше памяти и намного удобнее в использовании. NumPy использует гораздо меньше памяти для хранения данных и предоставляет механизм задания типов данных, который позволяет оптимизировать код еще дальше.

Что такое массив?

Массив является центральной структурой данных библиотеки NumPy. Это таблица значений, которая содержит информацию о необработанных данных, о том, как найти элемент и как интерпретировать элемент. Он имеет сетку элементов, которые можно проиндексировать в Все элементы имеют одинаковый тип, называемыймассив dtype(тип данных).

Массив может быть проиндексирован набором неотрицательных целых чисел, логическими значениями, другим массивом или целыми числами.рангмассива это количество измерений.формамассива — это кортеж целых чисел, дающий размер массива по каждому измерению.

Одним из способов инициализации массивов NumPy является использование вложенных списков Python.

a = np.array(, , ])

Мы можем получить доступ к элементам в массиве, используя квадратные скобки. Когда вы получаете доступ к элементам, помните, чтоиндексирование в NumPy начинается с 0, Это означает, что если вы хотите получить доступ к первому элементу в вашем массиве, вы получите доступ к элементу «0».

print(a)

Выход:

2.4.5. Двумерные массивы¶

Выше везде элементами массива были числа. Но на самом деле элементами
массива может быть что угодно, в том числе другие массивы. Пример:

a = 10, 20, 30
b = -1, -2, -3
c = 100, 200
z = a, b, c

Что здесь происходит? Создаются три обычных массива , и
, а потом создается массив , элементами которого являются как
раз массивы , и .

Что теперь получается? Например, — это элемент №1 массива
, т.е. . Но — это тоже массив, поэтому я могу написать
— это то же самое, что , т.е. (не забывайте,
что нумерация элементов массива идет с нуля). Аналогично,
и т.д.

То же самое можно было записать проще:

z = , -1, -2, -3], 100, 200]]

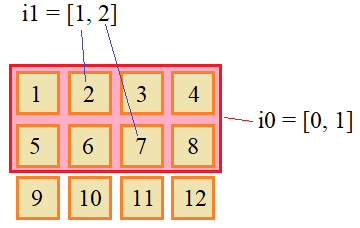
Получилось то, что называется двумерным массивом. Его можно себе еще
представить в виде любой из этих двух табличек:

Первую табличку надо читать так: если у вас написано , то
надо взять строку № и столбец №. Например, —
это элемент на 1 строке и 2 столбце, т.е. -3. Вторую табличку надо
читать так: если у вас написано , то надо взять столбец
№ и строку №. Например, — это элемент на 2
столбце и 1 строке, т.е. -3. Т.е. в первой табличке строка — это первый
индекс массива, а столбец — второй индекс, а во второй табличке
наоборот. (Обычно принято как раз обозначать первый индекс и
— второй.)

Когда вы думаете про таблички, важно то, что питон на самом деле не
знает ничего про строки и столбцы. Для питона есть только первый индекс
и второй индекс, а уж строка это или столбец — вы решаете сами, питону
все равно

Т.е. и — это разные вещи, и питон их
понимает по-разному, а будет 1 номером строки или столбца — это ваше
дело, питон ничего не знает про строки и столбцы. Вы можете как хотите
это решить, т.е. можете пользоваться первой картинкой, а можете и второй
— но главное не запутайтесь и в каждой конкретной программе делайте
всегда всё согласованно. А можете и вообще не думать про строки и
столбцы, а просто думайте про первый и второй индекс.

Обратите, кстати, внимание на то, что в нашем примере (массив,
являющийся вторым элементом массива ) короче остальных массивов (и
поэтому на картинках отсутствует элемент в правом нижнем углу). Это
общее правило питона: питон не требует, чтобы внутренние массивы были
одинаковой длины

Вы вполне можете внутренние массивы делать разной
длины, например:

x = , 5, 6], 7, 8, 9], [], 10]]

здесь нулевой массив имеет длину 4, первый длину 2, второй длину 3,
третий длину 0 (т.е. не содержит ни одного элемента), а четвертый длину
1. Такое бывает надо, но не так часто, в простых задачах у вас будут все
подмассивы одной длины.

Реверсив массив модуля массива в Python

Несмотря на то, что Python не поддерживает массивы, мы можем использовать Модуль массива Для создания массивных объектов различных типов данных. Хотя этот модуль обеспечивает много ограничений, когда речь идет о типе данных массива, он широко используется для работы с структурами данных массива в Python.

Теперь давайте посмотрим, как мы можем поместить массив в Python, созданный с модулем массива.

1. Использование обратного () метода

Подобно спискам, Способ также может быть использован для непосредственного изменения массива в Python модуля массива. Он меняет массив в своем первоначальном месте, поэтому не требует дополнительного места для хранения результатов.

import array

#The original array
new_arr=array.array('i',)
print("Original Array is :",new_arr)

#reversing using reverse()
new_arr.reverse()
print("Reversed Array:",new_arr)

Выход :

Original Array is : array('i', )
Resultant new reversed Array: array('i', )

2. Использование обратного () метода

Опять же Способ при прохождении с массивом, возвращает утечку с элементами в обратном порядке. Посмотрите на пример ниже, он показывает, как мы можем поместить массив, используя этот метод.

import array

#The original array
new_arr=array.array('i',)
print("Original Array is :",new_arr)

#reversing using reversed()
res_arr=array.array('i',reversed(new_arr))
print("Resultant Reversed Array:",res_arr)

Выход :

Original Array is : array('i', )
Resultant Reversed Array: array('i', )

Основы индексирования и срезы

Существует много способов выбора подмножества данных или элементов
массива. Одномерные массивы — это просто, на первый взгляд они
аналогичны спискам Python:

In : arr = np.arange(10)

In : arr
Out: array()

In : arr
Out: 5

In : arr
Out: array()

In : arr = 12

In : arr
Out: array()

Как видно, если присвоить скалярное значение срезу, как например,
, значение присваивается всем элементам среза. Первым
важным отличием от списков Python заключается в том, что срезы массива
являются представлениями исходного массива. Это означает, что данные
не копируются и любые изменения в представлении будут отражены в
исходном массиве.

Рассмотрим пример. Сначала создадим срез массива :

In : arr_slice = arr

In : arr_slice
Out: array()

Теперь, если мы изменим значения в массиве , то они
отразятся в исходном массиве :

In : arr_slice = 12345

In : arr
Out: 
array()

«Голый» срез присвоит все значения в массиве:

In : arr_slice = 64

In : arr
Out: array()

Поскольку NumPy был разработан для работы с очень большими массивами,
вы можете представить себе проблемы с производительностью и памятью,
если NumPy будет настаивать на постоянном копировании данных.

Замечание

Если вы захотите скопировать срез в массив вместо отображения, нужно
явно скопировать массив, например, .

С массивами более высокой размерности существует больше вариантов. В
двумерных массивах каждый элемент это уже не скаляр, а одномерный
массив.

In : arr2d = np.array(, , ])

In : arr2d
Out: array()

Таким образом, к отдельному элементу можно получить доступ
рекурсивно, либо передать разделенный запятыми список
индексов. Например, следующие два примера эквивалентны:

In : arr2d
Out: array()

In : arr2d[]
Out: 3

Если в многомерном массиве опустить последние индексы, то возвращаемый
объект будет массивом меньшей размерности. Например, создадим массив
размерности \( 2 \times 2 \times 3 \):

In : arr3d = np.array(, ], , ]])

In : arr3d
Out: 
array(,
        ],

       ,
        ]])

При этом — массив размерности \( 2 \times 3 \):

In : arr3d[]
Out: 
array(,
       ])

Можно присваивать как скаляр, так и массивы:

In : old_values = arr3d[].copy()

In : arr3d[] = 42

In : arr3d
Out: 
array(,
        ],

       ,
        ]])

In : arr3d[] = old_values

In : arr3d
Out: 
array(,
        ],

       ,
        ]])

Аналогично, возвращает все значения, чьи индексы
начинаются с , формируя одномерный массив:

In : arr3d
Out: array()

Это выражение такое же, как если бы мы проиндексировали в два этапа:

In : x = arr3d

In : x
Out: 
array(,
       ])

In : x[]
Out: array()

Индексирование с помощью срезов

Как одномерные объекты, такие как списки, можно получать срезы
массивов посредством знакомого синтаксиса:

In : arr
Out: array()

In : arr
Out: array()

Рассмотрим введенный выше двумерный массив . Получение срезов
этого массива немного отличается от одномерного:

In : arr2d
Out: 
array(,
       ,
       ])

In : arr2d
Out: 
array(,
       ])

Как видно, мы получили срез вдоль оси 0, первой оси. Срез, таким
образом, выбирает диапазон элементов вдоль оси. Выражение
можно прочитать как «выбираем первые две строки массива ».

Можно передавать несколько срезов:

In : arr2d
Out: 
array(,
       ])

При получении срезов мы получаем только отображения массивов того же
числа размерностей. Используя целые индексы и срезы, можно получить
срезы меньшей размерности:

In : arr2d
Out: array()

In : arr2d
Out: array()

Смотрите рис. .

Рисунок 1: Срезы двумерного массива

Python lists vs arrays

Lists	Arrays
Python lists are flexible and can hold arbitrary data.	Python arrays are just a thin wrapper on C arrays.
The list is part of python, so they do not need to be declared first.	Arrays need to be imported or declared first from other libraries(i.e. numpy).
It cannot directly handle arithmetic operations.	Can directly handle arithmetic operations.
Preferred for shorter sequences of data items.	Preferred for longer sequences of data items.
Greater flexibility allows easy modification of data.	Less flexibility since addition, deletion has to be done element-wise.
Consume larger memory for easy addition of elements.	Comparatively more compact in memory size.

Функции для создания массивов

Есть больше удобных функций для создания массивов фиксированного размера, с которыми вы можете столкнуться или которые вам необходимо использовать.

Давайте посмотрим на несколько. Вы можете увидеть полный список здесь:

Процедуры создания массива

пустой

Функция empty () создаст новый массив указанной формы.

Аргументом функции является массив или кортеж, который определяет длину каждого измерения создаваемого массива. Значения или содержимое созданного массива будут случайными и должны быть назначены перед использованием.

В приведенном ниже примере создается пустой трехмерный массив 3 × 3.

При выполнении примера печатается содержимое пустого массива. Ваше конкретное содержимое массива будет отличаться.

нули

Функция нулей () создаст новый массив указанного размера с содержимым, заполненным нулевыми значениями.

Аргументом функции является массив или кортеж, который определяет длину каждого измерения создаваемого массива.

В приведенном ниже примере создается нулевой двумерный массив размером 3 × 5.

При выполнении примера печатается содержимое созданного нулевого массива.

Ones

Функция ones () создаст новый массив указанного размера с содержимым, заполненным одним значением.

Аргументом функции является массив или кортеж, который определяет длину каждого измерения создаваемого массива.

В приведенном ниже примере создается одномерный массив из 5 элементов.

При выполнении примера печатается содержимое созданного массива.

Ways to print NumPy Array in Python

As mentioned earlier, we can also implement arrays in Python using the NumPy module. The module comes with a pre-defined array class that can hold values of same type.

These NumPy arrays can also be multi-dimensional. So, let us see how can we print both 1D as well as 2D NumPy arrays in Python.

Using print() method

Similar to the case of arrays implemented using lists, we can directly pass NumPy array name to the method to print the arrays.

import numpy as np

arr_2d = np.array(,,])
arr = np.array()

print("Numpy array is: ", arr) #printing the 1d numpy array

print("Numpy 2D-array is: ", arr_2d) #printing the 2d numpy array

Output:

Numpy array is:  
Numpy 2D-array is:  
 
 ]

Here, and are one 1D and one 2D NumPy arrays respectively. We pass their names to the method and print both of them. Note: this time also the arrays are printed in the form of NumPy arrays with brackets.

Using for loops

Again, we can also traverse through NumPy arrays in Python using loop structures. Doing so we can access each element of the array and print the same. This is another way to print an array in Python.

Look at the example below carefully.

import numpy as np

arr = np.array()
arr_2d = np.array(,,,])

#printing the numpy array
print("The Numpy Array is : ")
for i in arr:
    print(i, end = ' ')

#printing the numpy 2D-Array
print("\nThe Numpy 2D-Array is:")
for i in arr_2d:
    for j in i:
        print(j, end=" ")
    print()

Output:

The Numpy Array is : 
11 22 33 44 
The Numpy 2D-Array is:
90 20 
76 45 
44 87 
73 81

Here also we print the NumPy array elements in our desired way(without brackets) by accessing the elements of the 1D and 2D array individually.

Алгоритм быстрой сортировки

Этот алгоритм также использует разделяй и стратегию завоюйте, но использует подход сверху вниз вместо первого разделения массива вокруг шарнирного элемента (здесь, мы всегда выбираем последний элемент массива будут стержень).

Таким образом гарантируется, что после каждого шага точка поворота находится в назначенной позиции в окончательном отсортированном массиве.

Убедившись, что массив разделен вокруг оси поворота (элементы, меньшие точки поворота, находятся слева, а элементы, которые больше оси поворота, находятся справа), мы продолжаем применять функцию к остальной части, пока все элементы находятся в соответствующих позициях, когда массив полностью отсортирован.

def quicksort(a, arr_type):
    def do_partition(a, arr_type, start, end):
        # Performs the partitioning of the subarray a
        
        # We choose the last element as the pivot
        pivot_idx = end
        pivot = a

        # Keep an index for the first partition
        # subarray (elements lesser than the pivot element)
        idx = start - 1

        def increment_and_swap(j):
            nonlocal idx
            idx += 1
            a, a = a, a

         < pivot]
        
        # Finally, we need to swap the pivot (a with a)
        # since we have reached the position of the pivot in the actual
        # sorted array
        a, a = a, a

        # Return the final updated position of the pivot
        # after partitioning
        return idx+1

    def quicksort_helper(a, arr_type, start, end):
        if start < end:
            # Do the partitioning first and then go via
            # a top down divide and conquer, as opposed
            # to the bottom up mergesort
            pivot_idx = do_partition(a, arr_type, start, end)
            quicksort_helper(a, arr_type, start, pivot_idx-1)
            quicksort_helper(a, arr_type, pivot_idx+1, end)

    quicksort_helper(a, arr_type, 0, len(a)-1)

Здесь метод выполняет шаг подхода Divide and Conquer, в то время метод разделяет массив вокруг точки поворота и возвращает позицию точки поворота, вокруг которой мы продолжаем рекурсивно разбивать подмассив до и после точки поворота, пока не будет весь массив отсортирован.

Прецедент:

b = array.array('i', )
print('Before QuickSort ->', b)
quicksort(b, 'i')
print('After QuickSort ->', b)

Вывод:

Before QuickSort -> array('i', )
After QuickSort -> array('i', )

Представление массива

Итак, теперь мы знаем, как сделать копию массива посредством метода copy. Но бывают ситуации, когда нам не нужна копия массива, а нужен тот же массив но с иными размерами. Речь идёт, как вы уже догадались, о другом представлении исходного массива.

Для этих целей в NumPy есть метод ndarray.view(). Он создаёт новый объект массива, просматривающий данные исходного, однако изменение размеров одного массива не приводит к изменению размеров другого.

Обычно, функции которые меняют форму и порядок элементов в Пайтон-массивах возвращают не копию массива, а именно его представление:

Также представлениями массивов в Python являются срезы массивов:

Обратите внимание, что когда мы говорим о том, что массив b является представлением массива a, мы подразумеваем, что вне зависимости от вида и формы массива b он включает в себя те же данные в памяти, что и наш массив a. Таким образом, изменение элементов в одном из массивов приведёт, соответственно, к изменениям в другом

Разделение матрицы

Разделение одномерного массива NumPy аналогично разделению списка. Рассмотрим пример:

import numpy as np
letters = np.array()

# с 3-го по 5-ый элементы
print(letters)        # Вывод: 

# с 1-го по 4-ый элементы
print(letters)        # Вывод:    

# с 6-го до последнего элемента
print(letters)         # Вывод:

# с 1-го до последнего элемента
print(letters)          # Вывод:

# список в обратном порядке
print(letters)          # Вывод:

Теперь посмотрим, как разделить матрицу.

import numpy as np

A = np.array(, 
    ,
    ])

print(A)  # две строки, четыре столбца

''' Вывод:

 ]
'''


print(A)  # первая строка, все столбцы

''' Вывод:
` 1  4  5 12 14`
'''

print(A)  # все строки, второй столбец

''' Вывод:

'''

print(A)  # все строки, с третьего по пятый столбец
''' Вывод:

 
 ]
'''

Использование NumPy вместо вложенных списков значительно упрощает работу с матрицами. Мы рекомендуем детально изучить пакет NumPy, если вы планируете использовать Python для анализа данных.

Данная публикация является переводом статьи «Python Matrices and NumPy Arrays» , подготовленная редакцией проекта.

Обратитесь в массив списка в Python

Как мы уже обсуждали Списки и Массивы похожи в Python. Там, где основное различие между ними, в том, что массивы позволяют только элементы одного и того же типа данных, в то время как списки позволяют им быть разными.

Поскольку Python не поддерживает обычные массивы, мы можем использовать списки, чтобы изобразить то же самое и попытаться отменить их. Давайте посмотрим на разные методы, следующие, которые мы можем достичь этой задачи,

1. Использование списка нарезка, чтобы изменить массив в Python

Мы можем изменить массив списка, используя нарезка методы. Таким образом, мы фактически создаем новый список в обратном порядке как у оригинального. Давайте посмотрим, как:

#The original array
arr = 
print("Array is :",arr)

res = arr #reversing using list slicing
print("Resultant new reversed array:",res)

Выход :

Array is : 
Resultant new reversed array: 

2. Использование метода обратного ()

Python также предоставляет встроенный метод Это непосредственно меняет порядок элементов списка прямо на исходном месте.

Примечание : Таким образом, мы меняем порядок фактического списка. Следовательно, исходный порядок потерян.

#The original array
arr = 
print("Before reversal Array is :",arr)

arr.reverse() #reversing using reverse()
print("After reversing Array:",arr)

Выход :

Before reversal Array is : 
After reversing Array: 

3. Использование обратного () метода

У нас еще один метод, Что при прохождении со списком возвращает намерение имеющих только элементы списка в обратном порядке. Если мы используем Метод на этом намечном объекте мы получаем новый список, который содержит наш обратный массив.

#The original array
arr = 
print("Original Array is :",arr)
#reversing using reversed()
result=list(reversed(arr))
print("Resultant new reversed Array:",result)

Выход :

Original Array is : 
Resultant new reversed Array: 

2.4.8. Создание двумерного массива¶

Неожиданно нетривиальная операция на двумерных массивах — это создание
двумерного массива определенного размера, заполненного, например,
нулями. Вы помните, что одномерный массив длины можно создавать
как . Возникает желание написать , чтобы
создать двумерный массив размера (мы хотим, чтобы первый
индекс массива менялся от 0 до , а второй индекс до ,
поэтому это именно , а не ). Но это
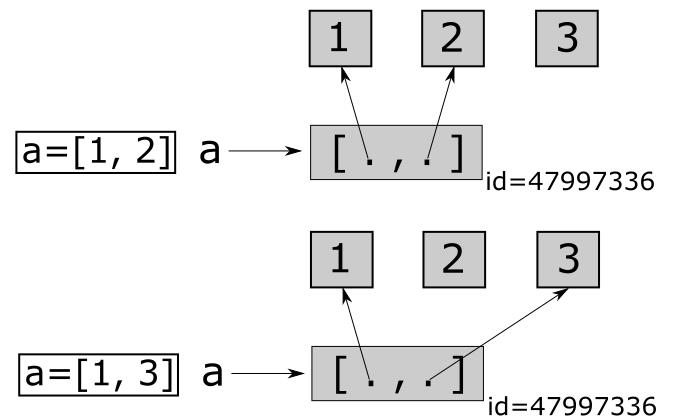
сработает не так, как вы можете думать. Дело опять в том, что в питоне
массивы по умолчанию не копируются полностью, поэтому то, что получается
— это массив длина , в котором каждый элемент соответствует
одному и тому же массиву длины . В итоге, если вы будете менять,
например, , то так же будет меняться и , и
и т.д. — т.к. все внутренние массивы на самом деле
соответствуют одному и тому же массиву.

Поэтому массив размера делается, например, так:

a = []
for i in range(n):
    a.append([ * m)

мы вручную раз приписали к массиву один и тот же массив.

Или еще есть магия в одну строчку:

a = 

Я пока не буду объяснять, как это работает, просто можете запомнить. Или
пользоваться предыдущим вариантом.