Числа. модуль и аргумент комплексного числа

Math Solution

Функциональный и удобный сервис, позволяющий выполнять сразу четыре  алгебраические операции: на сложение, вычитание, деление и умножение. Ознакомимся с основными рабочими этапами:

просмотрите правила ввода, кликнув на «+»;

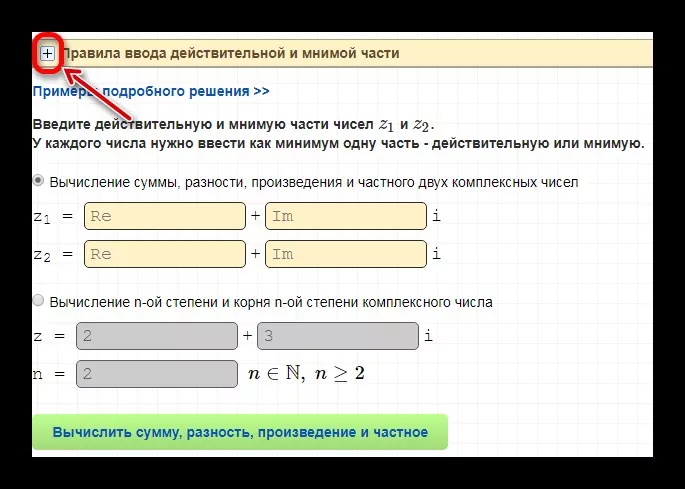
• введите необходимые значения;
• посчитайте, для этого есть специальная кнопка с вычислением;

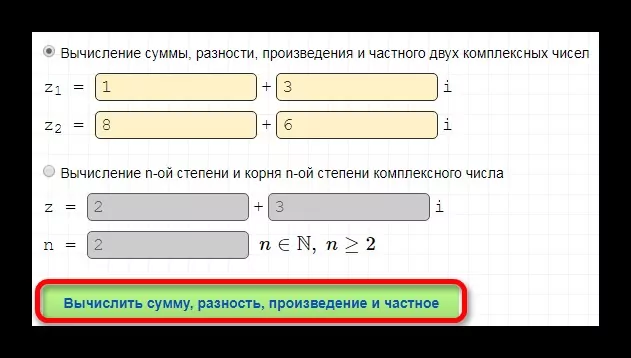
получите результат и подробное описание.

Этот ресурс станет настоящей находкой для старшеклассников. Легко заменит репетиторов и дорогие учебники. Подробное и понятное описание теории и принципов решения позволит быстро усвоить необходимый материал. Здесь вы не просто решаете задачи, используете онлайн калькулятор с подробным решением, но и можете легко понять, как это вычислялось.

Решение системы линейных уравнений

Наборы линейных уравнений довольно часто встречаются в повседневных расчетах, поэтому методов их решения придумано великое множество. Но перед рассмотрением самого простого алгоритма нахождения неизвестных стоит вспомнить о том, что вообще может иметь система таких уравнений:

— иметь только одно верное решение;

— иметь бесконечное множество корней;

— иметь несовместный тип (когда решений быть не может).

Метод Гаусса, используемый нашим АБАК-ботом — самое мощное и безотказное средство для поиска решения любой системы уравнений линейного типа.

Возвращаясь к терминам высшей математики, метод Гаусса можно сформулировать так: с помощью элементарных преобразований система уравнений должна быть приведена к равносильной системе треугольного типа (или т.н. ступенчатого типа), из которой постепенно, начиная с самого последнего уравнения, находятся оставшиеся переменные. При всем этом элементарные преобразования над системами — ровно то же самое, что и элементарные преобразования матриц в переложении для строк.

Наш бот умеет молниеносно выдавать решения системы линейных уравнений с неограниченным количеством переменных!

Практическое применение решение таких систем находит в электротехнике и геометрии: расчетах токов в сложных контурах и выведение уравнения прямой при пересечении трех плоскостей  а также в множестве специализированных задач.

Данный сервис позволяет решать неограниченную по размерам систему линейных уравнений с комплексными коэффициентами.

Практическое применение:

 

Ну, раз  бот умеет считать решения комплексных систем, то для него не составит труда считать частный случай, когда элементы системы являются вещественные числа. 

 

Второе, в школе Вам это наверняка не понадобится, но вот в институте, особенно институтах связи, при расчетах токов в сложных контурах в электротехнике, наверняка пригодится.

 

Извлечение корня.

Рассмотрим уравнение
$$
z^n=a,\label{ref22}
$$
где \(a\neq 0\) — комплексное число, \(n\) — натуральное число.

Если \(z=re^{i\varphi}, \ a=\rho e^{i\theta}\), то уравнение \eqref{ref22} примет вид
$$
r^n e^{in\varphi}=\rho e^{i\theta},\nonumber
$$
откуда
$$
r^n=\rho,\quad n\varphi=\theta+2k\pi,\quad k\in\mathbb{Z},\nonumber
$$
и поэтому
$$
r=\sqrt{\rho},\qquad \varphi_k=\frac{1}{n}(\theta+2k\pi),\quad k\in \mathbb{Z},\label{ref23}
$$
то есть числа
$$
z_k=\sqrt{\rho}e^{i\varphi_k}\label{ref24}
$$
являются корнями уравнения \eqref{ref22} и других корней это уравнение не имеет.

Заметим, что числа \(z_0,\ z_1,\ …,\ z_{n-1}\) различны, так как их аргументы \(\displaystyle\varphi_0=\frac{\theta}{n},\ \varphi_1=\frac{\theta}{n}+\frac{2\pi}{n},\ …,\ \varphi_{n-1}=\frac{\theta}{n}+\frac{2\pi(n-1)}{n}\) различны и отличаются друг от друга меньше, чем на \(2\pi\). Далее, \(z_n = z_0\), так как \(|z_n| = |z_0|=\displaystyle\sqrt{\rho}\) и \(\varphi_n=\varphi_0+2\pi\). Аналогично, \(z_{n+1} = z_1,\ z_{-1} = z_{n-1}\) и т. д.

Итак, при \(a\neq 0\) уравнение \eqref{ref22} имеет ровно \(n\) различных корней, определяемых формулами \eqref{ref23} и \eqref{ref24}, где \(k=0,1,…,n-1\).

На комплексной плоскости точки \(z_k\ (k=\overline{0,n-1})\) располагаются в вершинах правильного \(n\)-угольника, вписанного в окружность радиуса \(\displaystyle \sqrt{\rho}\) с центром в точке 0.

Пример 5.

Найти все корни уравнения \(z^4 = 1 + i\).

\(\triangle\) Корни \(z_k\ (k = \overline{0,3})\) этого уравнения определяются формулами \eqref{ref23} и \eqref{ref24}, где \(\displaystyle \rho=|1 + i| =\sqrt{2},\ \theta=\frac{\pi}{4}\), то есть
$$
z_k=\sqrt{2}e^{i\varphi_k},\nonumber
$$
где
$$
\varphi_k=\frac{\pi}{16}+\frac{\pi k}{2},\quad k=0,1,2,3.\nonumber
$$

Рис. 31.6

Точки \(z_k\) располагаются в вершинах квадрата (рис. 31.6). \(\blacktriangle\)

Сложение и вычитание комплексных чисел

Сложение и вычитание комплексных чисел — это безусловно, самая простая и понятная операция. Сложение/вычитание действительных частей комплексного числа переводит точку вправо/влево на действительной оси, а сложение/вычитание мнимых частей комплексного числа переводит точку вверх/вниз на мнимой оси.

Арифметически это работает так же, как объединение одинаковых членов в алгебре.

Например, если мы вычтем 1 — 4i из 3 + 2i, мы просто находим разницу действительных 3 — 1 = 2 и мнимых 2i — (-4i ) = 2i + 4i = 6i частей.

Это то же самое, что построить точку 3 + 2i и перенести ее влево на 1 единицу и вверх на 4 единицы. Получившаяся точка — это итоговый результат: 2 + 6i.

Также можно представить точки комплексной плоскости как вектор (Вектор – отрезок соединяющий две точки для которого указано, какая из его граничных точек является началом, а какая концом). В нашем случаем началом будет начало координат (0,0), а концом сама точка. Теперь внесём знак минус под скобки, чтобы у нас было сложение:

(3 + 2i) + (-1 + 4i)

И затем построим два вектора.

Чтобы узнать результат сложения перенесём параллельно начало одного вектора в конец второго. Поскольку сложение является коммутативным, не имеет значения, каким образом мы их складываем. a+b=b+а (свойство коммутативности)

Это может показаться излишним, но вот в чем дело: понимание векторного представления сделает умножение и деление комплексных чисел намного проще.

Возведение комплексных чисел в степень

Начнем со всеми любимого квадрата.

Пример 9

Возвести в квадрат комплексное число

Здесь можно пойти двумя путями, первый способ это переписать степень как произведение множителей  и перемножить числа по правилу умножения многочленов.

Второй способ состоит в применении известной школьной формулы сокращенного умножения :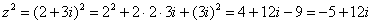

Для комплексного числа легко вывести свою формулу сокращенного умножения:. Аналогичную формулу можно вывести для квадрата разности, а также для куба суммы и куба разности. Но эти формулы более актуальны для задач комплексного анализа, поэтому на данном уроке я воздержусь от подробных выкладок.

Что делать, если комплексное число нужно возвести, скажем, в 5-ю, 10-ю или 100-ю степень? Ясно, что в алгебраической форме проделать такой трюк практически невозможно, действительно, подумайте, как вы будете решать пример вроде ?

И здесь на помощь приходит тригонометрическая форма комплексного числа и, так называемая, формула Муавра: Если комплексное число представлено в тригонометрической форме , то при его возведении в натуральную степень  справедлива формула:

Данная формула следует из правила умножения комплексных чисел, представленных в тригонометрической форме: чтобы найти произведение чисел ,  нужно перемножить их модули и сложить аргументы:

Аналогично для показательной формы: если , то:

Просто до безобразия.

Пример 10

Дано комплексное число , найти .

Что нужно сделать? Сначала нужно представить данное число в тригонометрической форме. Внимательные читатели заметили, что в Примере 8 мы это уже сделали:

Тогда, по формуле Муавра: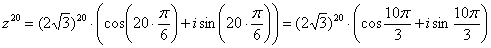

Упаси боже, не нужно считать на калькуляторе , а вот угол в большинстве случае следует упростить. Как упростить? Образно говоря, нужно избавиться от лишних оборотов. Один оборот составляет  радиан или 360 градусов. Выясним сколько у нас оборотов в аргументе . Для удобства делаем дробь правильной: , после чего становится хорошо видно, что можно убавить один оборот: . Надеюсь всем понятно, что  и  – это один и тот же угол.

Таким образом, окончательный ответ запишется так:

Любители стандартов везде и во всём могут переписать ответ в виде: (т.е. убавить еще один оборот и получить значение аргумента в стандартном виде).

Хотя  – ни в коем случае не ошибка.

Пример 11

Дано комплексное число , найти . Полученный аргумент (угол) упростить, результат представить в алгебраической форме.

Это пример для самостоятельного решения, полное решение и ответ в конце урока.

Отдельная разновидность задачи возведения в степень – это возведение в степень чисто мнимых чисел.

Пример 12

Возвести в степень комплексные числа , ,

Здесь тоже всё просто, главное, помнить знаменитое равенство.

Если мнимая единица возводится в четную степень, то техника решения такова:

Если мнимая единица возводится в нечетную степень, то «отщипываем» одно «и»,  получая четную степень:

Если есть минус (или любой действительный коэффициент), то его необходимо предварительно отделить:

Пример 13

Возвести в степень комплексные числа ,

Это пример для самостоятельного решения.

Комплекснозначные функции действительного переменного.

Если каждому значению \(t\in \) поставлено в соответствие комплексное число \(z=z(t)\), то говорят, что на отрезке \(\) задана комплекснозначная функция действительного переменного.

Пусть \(\operatorname{Re}z(t) = x(t),\ \operatorname{Im}z(t) = y(t)\), тогда \(z(t) = x(t)+iy(t)\). Функцию \(z(t)\) можно рассматривать как вектор-функцию \(z(t)=(x(t),y(t))\). Определения предела, непрерывности, производной для комплекснозначной функции аналогичны соответствующим определениям для вектор-функции.

Например, производная функции \(z(t) = x(t) + iy(t)\) определяется формулой
$$
z'(t) = x'(t) + iy'(t).\label{ref25}
$$
Следовательно, производная \(z'(t)\) существует, если существуют производные \(x'(t)\) и \(y'(t)\).

Применяя формулу \eqref{ref25} к функции \(e^{it}=\cos t+i\sin t\), получаем \((e^{it})’=-\sin t+i\cos t=i^2\sin t + i\cos t = i(\cos t + i\sin t)\), то есть
$$
(e^{it})’=i e^{it}.\label{ref26}
$$

Таким образом, формула для производной комплексной функции \(e^{it}\) имеет такой же вид, как и для функции \(e^{\alpha t}\), где \(\alpha\in\mathbb{R}\).

Определим теперь показательную функцию \(\displaystyle e^{(\alpha+i\beta)t}\), где \(\alpha,\beta\) — заданные действительные числа, \(t\) — действительное переменное. Функция \(f(t) = e^t\), где \(t\in\mathbb{R}\), удовлетворяет условию
$$
f(t_1)f(t_2) = f(t_1+t_2).\label{ref27}
$$

Аналогично функция \(e^{i\beta t}\), где \(\beta\in\mathbb{R}\), обладает свойством \eqref{ref27} в силу первого из равенств \eqref{ref18}.

Поэтому функцию    \(e^{(\alpha+i\beta)t}\) естественно определить так, чтобы для нее выполнялось условие \eqref{ref27}, то есть
$$
e^{(\alpha+i\beta)t}=e^{\alpha t}e^{i\beta t}.\nonumber
$$

Используя формулу \eqref{ref15}, отсюда находим
$$
e^{(\alpha+i\beta)t} = e^{\alpha t} (\cos \beta t+i\sin\beta t).\label{ref28}
$$
Применяя к функции \(e^{\lambda t}\), где \(\lambda=\alpha+i\beta\), правило дифференцирования \eqref{ref25}, легко показать, что
$$
(e^{\lambda t})=\lambda e^{\lambda t},\quad \lambda=\alpha+i\beta.\label{ref29}
$$

По аналогии с производной неопределенный интеграл от комплекснозначной функции \(z(t)=x(t)+iy(t)\) определяется формулой
$$
\int z(t) dt = \int x(t) dt + i\int y(t) dt.\nonumber
$$

Если комплексная функция \(\omega(t) = \xi(t) + i\eta (t)\) такова, что \(\omega'(t)=z(t)\), то
$$
\int z(t)=\int \omega'(t)dt=\int \xi'(t)dt+i\int \eta'(t)dt = \xi(t) + C_1 + i\eta(t)+iC_2.\nonumber
$$
Следовательно,
$$
\int z(t) dt = \omega(t) + C,\quad C = C_1+iC_2.\nonumber
$$
Применяя это утверждение к функции \(e^{(\alpha+i\beta)t}\) и используя формулу \eqref{ref29}, получаем
$$
\int e^{(\alpha+i\beta)t}=\displaystyle \frac{e^{(\alpha+i\beta)t}}{\alpha+i\beta}+C_1+iC_2.\label{ref30}
$$

Выделяя в равенстве \eqref{ref30} действительные и мнимые части, находим
$$
\int e^{\alpha t}\cos\beta t dt + i\int e^{\alpha t}\sin\beta t dt = \frac{\alpha-i\beta}{\alpha^2+\beta^2}e^{\alpha t}(\cos\beta t+i\sin\beta t)+C_1+C_2,\nonumber
$$
откуда получаем
$$
\int e^{\alpha t}\cos\beta t dt=\frac{e^{\alpha t}}{\alpha^2+\beta^2}(\alpha\cos\beta t+\beta\sin\beta t)+C_1,\label{ref31}
$$
$$
\int e^{\alpha t}\sin\beta t dt=\frac{e^{\alpha t}}{\alpha^2+\beta^2}(\alpha\sin\beta t-\beta\cos\beta t)+C_2,\label{ref32}
$$

Заметим, что формула \eqref{ref31} была получена с помощью в .

Деление комплексных чисел

Как и при любом делении в алгебре, комплексное число нельзя делить на нуль
и на комплексное число .

При делении комплексного числа на действительное число на это число нужно
разделить и действительную, и мнимую компоненты. При делении комплексного числа на
комплексное число нужно делимое и делитель умножить на число, сопряжённое делителю.

Пример 9. Разделить комплексное число
на комплексное число
.

Решение. Умножив числитель и знаменатель дроби
на , получаем:

Автор проекта был свидетелем вопроса о том, откуда взялось 5 в знаменателе дроби.
Пояснения вызывают реакцию «А слона-то я и не заметил!». Пояснения следующие: не забываем, что мы
имеем дело с комплексными числами и знаем, что — это
не какая-нибудь переменная, а корень из минус единицы. Таким образом,

.

Пример 10. Разделить комплексное число
на комплексное число
.

Решение. Умножив числитель и знаменатель дроби
на , получаем:

Если всё же возникает вопрос, откуда в знаменателе дроби 10, смотрите пояснения в
конце предыдущего примера.

Алгебраическая форма комплексного числа. Сложение, вычитание, умножение и деление комплексных чисел

С алгебраической формой комплексного числа мы уже познакомились,  – это и есть алгебраическая форма комплексного числа. Почему речь зашла о форме? Дело в том, что существуют еще тригонометрическая и показательная форма комплексных чисел, о которых пойдет речь в следующем параграфе.

Действия с комплексными числами не представляют особых сложностей и мало чем отличаются от обычной алгебры.

Сложение комплексных чисел

Пример 1

Сложить два комплексных числа ,

Для того чтобы сложить два комплексных числа нужно сложить их действительные и мнимые части:

Просто, не правда ли? Действие настолько очевидно, что не нуждается в дополнительных комментариях.

Таким нехитрым способом можно найти сумму любого количества слагаемых: просуммировать действительные части и просуммировать мнимые части.

Для комплексных чисел справедливо правило первого класса:  – от перестановки слагаемых сумма не меняется.

Вычитание комплексных чисел

Пример 2

Найти разности комплексных чисел  и , если ,

Действие аналогично сложению, единственная особенность состоит в том, что вычитаемое нужно взять в скобки, а затем – стандартно раскрыть эти скобки со сменой знака:

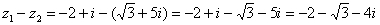
Результат не должен смущать, у полученного числа две, а не три части. Просто действительная часть – составная: . Для наглядности ответ можно переписать так: .

Рассчитаем вторую разность: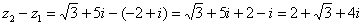
Здесь действительная часть тоже составная:

Чтобы не было какой-то недосказанности, приведу короткий пример с «нехорошей» мнимой частью: . Вот здесь без скобок уже не обойтись.

Умножение комплексных чисел

Настал момент познакомить вас со знаменитым равенством:

Пример 3

Найти произведение комплексных чисел  ,

Очевидно, что произведение следует записать так:

Что напрашивается? Напрашивается раскрыть скобки по правилу умножения многочленов. Так и нужно сделать! Все алгебраические действия вам знакомы, главное, помнить, что  и быть внимательным.

Повторим, omg, школьное правило умножения многочленов: Чтобы умножить многочлен на многочлен нужно каждый член одного многочлена умножить на каждый член другого многочлена.

Я распишу подробно: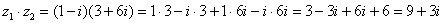

Надеюсь, всем было понятно, что

Внимание, и еще раз внимание, чаще всего ошибку допускают в знаках. Как и сумма, произведение комплексных чисел перестановочно, то есть справедливо равенство:

Как и сумма, произведение комплексных чисел перестановочно, то есть справедливо равенство: .

В учебной литературе и на просторах Сети легко найти специальную формулу для вычисления произведения комплексных чисел. Если хотите, пользуйтесь, но мне кажется, что подход с умножением многочленов универсальнее и понятнее. Формулу приводить не буду, считаю, что в данном случае – это забивание головы опилками.

Деление комплексных чисел

Пример 4

Даны комплексные числа , . Найти частное .

Составим частное:

Деление чисел осуществляется методом умножения знаменателя и числителя на сопряженное знаменателю выражение.

Вспоминаем бородатую формулу  и смотрим на наш знаменатель: . В знаменателе уже есть , поэтому сопряженным выражением в данном случае является , то есть

Согласно правилу, знаменатель нужно умножить на , и, чтобы ничего не изменилось, домножить числитель на то же самое число :

Далее в числителе нужно раскрыть скобки (перемножить два числа по правилу, рассмотренному в предыдущем пункте). А в знаменателе воспользоваться формулой  (помним, что и не путаемся в знаках!!!).

Распишу подробно:

Пример я подобрал «хороший», если взять два числа «от балды», то в результате деления почти всегда получатся дроби, что-нибудь вроде .

В ряде случаев перед делением дробь целесообразно упростить, например, рассмотрим частное чисел: . Перед делением избавляемся от лишних минусов: в числителе и в знаменателе выносим минусы за скобки и сокращаем эти минусы: . Для любителей порешать приведу правильный ответ:

Редко, но встречается такое задание:

Пример 5

Дано комплексное число . Записать данное число в алгебраической форме (т.е. в форме ).

Приём тот же самый – умножаем знаменатель и числитель на сопряженное знаменателю выражение. Снова смотрим на формулу . В знаменателе уже есть , поэтому знаменатель и числитель нужно домножить на сопряженное выражение , то есть на :

Пример 6

Даны два комплексных числа , . Найти их сумму, разность, произведение и частное.

Это пример для самостоятельного решения. Полное решение и ответ в конце урока.

На практике запросто могут предложить навороченный пример, где нужно выполнить много действий с комплексными числами. Никакой паники: будьте внимательны, соблюдайте правила алгебры, обычный алгебраический порядок действий, и помните, что

Мир математики

Достойный внимания сайт, предоставляющий после полученного ответа подробные пояснения. Работать с ним также очень легко:

вводите условия в соответствующие поля;

• выбираете нужное действие;
• после нажатия на выбранную операцию будет начато вычисление и выдан результат.

Здесь вы найдете при необходимости подробную инструкцию для работы, так что точно не запутаетесь. Доступны разные варианты вычислительных сервисов, к примеру, матричный, инженерный и прочие.

Полезный контент:

• Формат heic, чем открыть, что это такое?
• Перевод с английского на русский с транскрипцией — лучшие онлайн сервисы
• Видеодрайвер перестал отвечать и был восстановлен — что за ошибка?
• Запись видео с экрана компьютера — какие программы в этом помогут?
• Караоке онлайн петь бесплатно с баллами — какие сервисы в этом помогут

Примеры

linur_i 5:2 3 10 2 -11:3 0:-30

Корни системы линейных уравнений равны следующим значениям.

Переменные считаются слева направо

1.4389598942265:-1.941383869546

-0.3591890700749:2.2763331864257

 то есть x1=1.4389598942265 — 1.941383869546 i 

x2=-0.3591890700749+2.2763331864257 i

Рассчитаем комплексную систему линейных уравнений

такого вида

Записываем все элементы в поле ввода. Как видите, данные могут быть не только числовые но и быть произвольным выражением, включающее в себя комплексные числа.

И получаем следующий результат.

Вы ввели следующую систему уравнений

Решение системы следующее

Успехов в расчетах !

• Скалярное произведение двух матриц >>

Аргумент комплексного числа

      Рассмотрим радиус–вектор произвольного, но отличного от нуля, комплексного числа   z.

      Аргументом комплексного числа z называют угол φ между положительным направлением вещественной оси и радиус-вектором    z.

      Аргумент комплексного числа  z  считают положительным, если поворот от положительного направления вещественной оси к  радиус-вектору z  происходит против часовой стрелки, и отрицательным  — в случае поворота по часовой стрелке (см. рис.).

      Считается, что комплексное число нуль аргумента не имеет.

      Поскольку аргумент любого комплексного числа определяется с точностью до слагаемого 2kπ , где  k  — произвольное целое число, то вводится, главное значение аргумента, обозначаемое   arg z   и удовлетворяющее неравенствам:

      Тогда оказывается справедливым равенство:

      Если для комплексного числа   z = x + i y   нам известны его модуль   r = | z | и его аргумент φ, то мы можем найти вещественную и мнимую части по формулам

(3)

      Если же комплексное число   z = x + i y   задано в алгебраической форме, т.е. нам известны числа   x   и   y,   то модуль этого числа, конечно же, определяется по формуле

(4)

а аргумент определяется в соответствии со следующей Таблицей 1.

      Для того, чтобы не загромождать запись, условимся, не оговаривая этого особо, символом  k  обозначать в Таблице 1 произвольное целое число.

      Таблица 1. – Формулы для определения аргумента числа   z = x + i y

Расположениечисла  z	Знаки x и y	Главное значение аргумента	Аргумент	Примеры
Положительная вещественнаяполуось	x > 0 , y = 0	φ = 2kπ
	x > 0 , y > 0
Положительнаямнимаяполуось	x = 0 , y > 0
	x < 0 , y > 0
Отрицательнаявещественнаяполуось	x < 0 , y = 0	π	φ = π + 2kπ
	x < 0 , y < 0
Отрицательнаямнимаяполуось	x = 0 , y < 0
	x > 0 , y < 0

Расположениечисла  z	Положительнаявещественнаяполуось
Знаки x и y	x > 0 , y = 0
Главноезначениеаргумента
Аргумент	φ = 2kπ
Примеры

Расположениечисла  z
Знаки x и y	x > 0 , y > 0
Главноезначениеаргумента
Аргумент
Примеры

Расположениечисла  z	Положительнаямнимаяполуось
Знаки x и y	x = 0 , y > 0
Главноезначениеаргумента
Аргумент
Примеры

Расположениечисла  z
Знаки x и y	x < 0 , y > 0
Главноезначениеаргумента
Аргумент
Примеры

Расположениечисла  z	Отрицательнаявещественнаяполуось
Знаки x и y	x < 0 , y = 0
Главноезначениеаргумента	π
Аргумент	φ = π + 2kπ
Примеры

Расположениечисла  z
Знаки x и y	x < 0 , y < 0
Главноезначениеаргумента
Аргумент
Примеры

Расположениечисла  z	Отрицательнаямнимаяполуось
Знаки x и y	x = 0 , y < 0
Главноезначениеаргумента
Аргумент
Примеры

Расположениечисла  z
Знаки x и y	x < 0 , y < 0
Главноезначениеаргумента
Аргумент
Примеры

Расположение числа   z : Положительная вещественная полуось Знаки x и y : x > 0 ,   y = 0 Главное значение аргумента: Аргумент: φ = 2kπ Примеры:

Расположение числа   z : Знаки x и y : x > 0 ,   y > 0 Главное значение аргумента: Аргумент: Примеры:

Расположение числа   z : Положительная мнимая полуось Знаки x и y : x = 0 ,   y > 0 Главное значение аргумента: Аргумент: Примеры:

Расположение числа   z : Знаки x и y : x < 0 ,   y > 0 Главное значение аргумента: Аргумент: Примеры:

Расположение числа   z : Отрицательная вещественная полуось Знаки x и y : x < 0 ,   y = 0 Главное значение аргумента: π Аргумент: φ = π + 2kπ Примеры:

Расположение числа   z : Знаки x и y : x < 0 ,   y < 0 Главное значение аргумента: Аргумент: Примеры:

Расположение числа   z : Отрицательная мнимая полуось Знаки x и y : x = 0 ,   y < 0 Главное значение аргумента: Аргумент: Примеры:

Расположение числа   z : Знаки x и y : x < 0 ,   y < 0 Главное значение аргумента: Аргумент: Примеры: